Magic Hexagon

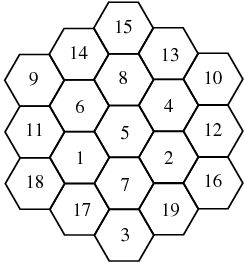
A magic hexagon of order 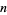 is an arrangement of close-packed hexagons containing the numbers 1, 2, ...,
is an arrangement of close-packed hexagons containing the numbers 1, 2, ..., 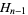 , where
, where 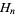 is the
is the 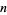 th hex number such that the numbers along each straight line add up to the same sum. (Here, the hex numbers are i.e., 1, 7, 19, 37, 61, 91, 127, ...; OEIS A003215). In the above magic hexagon of order
th hex number such that the numbers along each straight line add up to the same sum. (Here, the hex numbers are i.e., 1, 7, 19, 37, 61, 91, 127, ...; OEIS A003215). In the above magic hexagon of order 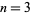 , each line (those of lengths 3, 4, and 5) adds up to 38.
, each line (those of lengths 3, 4, and 5) adds up to 38.
It was discovered independently by Ernst von Haselberg in 1887 (Bauch 1990, Hemme 1990), W. Radcliffe in 1895 (Tapson 1987, Hemme 1990, Heinz), H. Lulli (Hendricks, Heinz), Martin Kühl in 1940 (Gardner 1963, 1984; Honsberger 1973), Clifford W. Adams, who worked on the problem from 1910 to 1957 (Gardner 1963, 1984; Honsberger 1973), and Vickers (1958; Trigg 1964).
This problem and the solution have a long history. Adams came across the problem in 1910. He worked on the problem by trial and error and after many years arrived at the solution which he transmitted to M. Gardner, Gardner sent Adams' magic hexagon to Charles W. Trigg, who by mathematical analysis found that it was unique disregarding rotations and reflections (Gardner 1984, p. 24). Adams' result and Trigg's work were written up by Gardner (1963). Trigg (1964) did further research and summarized known results and the history of the problem.
Trigg showed that the magic constant for an order 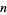 hexagon would be
hexagon would be
the first few of which are 1, 28/3, 38, 703/7, 1891/9, 4186/11, ... (OEIS A097361 and A097362), which requires 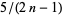 to be an integer for a solution to exist. But this is an integer for only
to be an integer for a solution to exist. But this is an integer for only 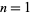 (the trivial case of a single hexagon) and Adams's
(the trivial case of a single hexagon) and Adams's 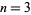 (Gardner 1984, p. 24).
(Gardner 1984, p. 24).
SEE ALSO:Hex Number,
Hexagon,
Magic Graph,
Magic Hexagram,
Magic Square,
Pascal's Theorem,
Talisman Hexagon
REFERENCES:
Abraham, K. Philadelphia Evening Bulletin. July 19, 1963, p. 18 and July 30, 1963.
Bauch, H. F. "Zum magischen Sechseck von Ernst v. Haselberg." Wissenschaft und Fortschritt 40, 240-242 and 4th page of dustjacket, 1990.
Bauch, H. F. "Magische Figuren in Parketten." Math. Semesterber. 38, 99-115, 1991.
Beeler, M. et al. Item 49 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 18, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item49.
Berlekamp, E. R.; Conway, J. H; and Guy, R. K. Winning Ways for Your Mathematical Plays, Vol. 2: Games in Particular. London: Academic Press, 1982.
Gardner, M. "Permutations and Paradoxes in Combinatorial Mathematics." Sci. Amer. 209, 112-119, Aug. 1963.
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. 22-24, 1984.
Gardner, M. "Hexes and Stars." Ch. 2 in Time Travel and Other Mathematical Bewilderments. New York: W. H. Freeman, pp. 15-24, 1988.
Heinz, H. D. "More Magic Squares." https://www.magic-squares.net/moremsqrs.htm.
Hemme, H. "Das magische Sechseck." Bild der Wissenschaft, 164-166, Oct. 1988. Reprinted as "Das magische Sechseck." §1.6 in Das Beste aus dem Mathematischen Kabinett (Ed. T. Devendran). Stuttgart, Germany: Deutsche Verlag-Anstalt, pp. 36-41, 1990.
Hemme, H. "Das magische Sechseck." Problem 88 in Mathematik zum Frühstück. Göttingen, Germany: Vandenhoeck & Ruprecht, p. 44, 1990.
Hendricks, J. "A Magic Square Course." p. 7.
Honsberger, R. Mathematical Gems I. Washington, DC: Math. Assoc. Amer., pp. 69-76, 1973.
Kschischang, F. R. "The Magic Hexagon." Sept. 2000. https://www.comm.toronto.edu/~frank/hexagon/proof.html.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 100-101, 1979.
Pickover, C. A. "The Magic Hexagon." §139 in The Zen of Magic Squares, Circles, and Stars: An Exhibition of Surprising Structures Across Dimensions. Princeton, NJ: Princeton University Press, pp. 325-340, 2002.
Radcliffe, W. "Magic Hexagon." 1895. https://www.johnrausch.com/PuzzleWorld/puz/magic_hexagon.htm.
Sloane, N. J. A. Sequences A003215/M4362, A097361, and A097362 in "The On-Line Encyclopedia of Integer Sequences."
Tapson, F. "The Magic Hexagon: An Historical Note." Math. Gaz. 71, 217-229, Oct. 1987.
Trigg, C. W. "A Unique Magic Hexagon." Recr. Math. Mag. 46, 40-43, Jan./Feb. 1964. https://www.mathematik.uni-bielefeld.de/~sillke/PUZZLES/magic-hexagon-trigg.
Trigg, C. W. "P824: A Well-Known Magic Hexagon." Math. Mag. 45, 100, 1972.
Trigg, C. W. "Solution to Problem P824." Math. Mag. 46, 44-45, 1973.
Vickers, T. "Magic Hexagon." Math. Gaz. 42, 291, Dec. 1958.
von Haselberg, E. "Problem and Solution of the Unique Magic Hexagon of Order 3." Manuscript, 1887.
von Haselberg, E. "Aufgabe." §795 in Zeitschrift für mathematische und naturwissenschaftlichen Unterricht 19, 429, 1888.
von Haselberg, E. "Auflösung." §801 in Zeitschrift für mathematische und naturwissenschaftlichen Unterricht 20, 263-264, 1889.
Referenced on Wolfram|Alpha:
Magic Hexagon
CITE THIS AS:
Weisstein, Eric W. "Magic Hexagon." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/MagicHexagon.html

