|
Reply |
Message 1 of 35 on the subject |
|
|
Geometry
Geometry of the Great Pyramid
DIMENSIONS of Great Pyramid
by morphvs
The following article is Copyright © 2001-2003 aiwaz.net_institute.
All rights reserved. No part of this website, including text and images, may be reproduced or copied
in any form or by any means without the express prior written permission of aiwaz.net_institute.
Presented with permission.
If the calculations concerning the royal cubit are correct the main dimensions of the pyramid should also prove that. The approximate dimensions of the pyramid are calculated by Petrie according to the remains of the sockets in the ground for the casing stones whose remains are still at the top of the pyramid, and the angle 51° 52' ± 2' of the slopes. The base of 9069 inches is approximately 440 royal cubits (the difference is 9 inches which is not a remarkable difference if we consider the whole dimension and consider that the employed data represent only an estimation of the real values) whereas the calculated height, 5776 inches, is precisely 280 royal cubits. The relation 440:280 can be reduced to 11:7, which gives an approximation of the half value of Pi.
Squaring the Circle

The circle and the square are
united through the circumference:
440x4=1760=2x22/7x280
area of square: 440x440=193600
area of circle:28x28x22/7=246400
sum: 440000
|
The engagement of Pi value in the main dimensions suggests also a very accurate angle of 51° 52' ± 2' of the slopes which expresses the value of Pi. Another coincidence is the relation between the height of the pyramid's triangle in relation to a half of the side of the pyramid, since it appears to be the Golden Section, or the specific ratio ruling this set of proportions, F = (sqr(5)+1)/2 = 1.618 = 356:220. This ratio, 356:220 = 89:55 is also contained in the first of Fibonacci Series:
1 2 3 5 8 13 21 34 55 89 144 ...
A single composition contains two apparently contradicting irrational numbers P and F, without disrupting each other. This appears to be completely opposed to the classical architectural canon which postulates that in 'good' composition no two different geometrical systems of proportions may be mixed in order to maintain the purity of design.
But analysis of other architectural and artistic forms suggested that the greatest masters skillfully juggled the proportional canons without losing the coherent system, for they knew that these systems can be interconnected if the path that links them is found. That is obvious In the case of the Great Pyramid where two different principles are interweaved without interference ruling different angles of the composition, which is most importantly a most simple one, namely 11:7, a most simple ratio obviously signifying such infinite mysteries as the value of P and most 'natural' value of F. In spite of common miss-understanding of architectural composition, the most mysterious and praised compositions are very simple but not devoid of anthropomorphic appeal, since everything is made out of human proportions, just like Vitruvius describing the rations of the human body, very simple and very clean. The numbers 7 and in 11 are successive factors in the second of Fibonacci progressions that approximate geometry of the pentagram:
1 3 4 7 11 18 29 47 76 123 ...
The summary of the selected main mean dimensions is:
|
dimension
|
b. inch
|
m
|
royal cub.
|
palm
|
digit
|
|
base
|
9068.8
|
230.35
|
440
|
3,080
|
12,320
|
|
height
|
5776
|
146.71
|
280
|
1,960
|
7,840
|
|
sum
|
|
|
720
|
|
20,160
|
|
slope
|
7343.2
|
186.52
|
356
|
2,492
|
9,968
|
|
edge
|
8630.4
|
219.21
|
418
|
2,926
|
11,704
|

The main source of all kinds of delusions and speculations about our mythical past for the western man comes of course from Plato. With the myth of Atlantis he planted the necessary seed of mythical Eden, a culture of high intelligence that lived before the known history. If Plato received any wisdom from the ancient Egypt it could perhaps be traced in the canon of numbers that is so latently present throughout his work, but never on the surface. This canon seems to appear in the descriptions of his fantastic cities where everything is most carefully calculated and proportioned. The topic of Plato's Laws is the description of the ideal state called Magnesia which is entirely composed out of the mysterious number 5,040.
The distance* when Earth is closest to Sun (perihelion) is 147x106 km, which is translated into royal cubits 280x109, hinting at the height of the Great pyramid,
280 royal cubits.
The above article comes from aiwaz.net_institute - Great Pyramid and Giza plateau
and is Copyright © 2001-2003 aiwaz.net_institute. All rights reserved.
No part of this article, including text and images, may be reproduced or copied in any form
or by any means without the express prior written permission of aiwaz.net_institute. Reprinted with permission.
* Related links: Astronomic & Cosmographic Data, Nasa site with planetary data
Do not miss this web site: aiwaz.net_institute - Great Pyramid and Giza plateau
Find out more amazing facts about the GREAT PYRAMID: Position of King's Chamber, Queen's Chamber, Subterranean Chamber; SECOND PYRAMID: Dimensions of Pyramid, Great Chamber, Coffer, Lower Chamber; THIRD PYRAMID: Dimensions of Pyramid, Chambers,MATHESIS of Giza Plateau.
The Golden Ratio & Squaring the Circle in the Great Pyramid
A straight line is said to have been cut in extreme and mean ratio when,
as the whole line is to the greater segment, so is the greater to the less. [Euclid]
The extreme and mean ratio is also known as the golden ratio.

If the smaller part = 1, and larger part = G, the golden ratio requires that
G is equal approximately 1.6180
Does the Great Pyramid contain the Golden Ratio?
Assuming that the height of the GP = 146.515 m, and base = 230.363 m, and using simple math
we find that half of the base is 115.182 m and the "slant height" is 186.369 m
Dividing the "slant height" (186.369m) by "half base" (115.182m) gives = 1.6180, which is practically equal to the golden ration!
The earth/moon relationship is the only one in our solar system that contains this unique golden section ratio that "squares the circle". Along with this is the phenomenon that the moon and the sun appear to be the same size, most clearly noticed during an eclipse. This too is true only from earth's vantage point…No other planet/moon relationship in our solar system can make this claim.
Although the problem of squaring the circle was proven mathematically impossible in the 19th century (as pi, being irrational, cannot be exactly measured), the Earth, the moon, and the Great Pyramid, are all coming about as close as you can get to the solution!
If the base of the Great Pyramid is equated with the diameter of the earth, then the radius of the moon can be generated by subtracting the radius of the earth from the height of the pyramid (see the picture below).

Click here to view larger picture.
Also the square (in orange), with the side equal to the radius of the Earth, and the circle (in blue),
with radius equal to the radius of the Earth plus the radius of the moon, are very nearly equal in perimeters:
Orange Square Perimeter = 2+2+2+2=8
Blue Circle Circumference = 2*pi*1.273=8
Note:
Earth, Radius, Mean = 6,370,973.27862 m *
Moon, Radius, Mean = 1,738,000 m.*
Moon Radius divided by Earth Radius = 0.2728 *
* Source: Astronomic and Cosmographic Data
Let's re-phrase the above arguments **

In the diagram above, the big triangle is the same proportion and angle of the Great Pyramid, with its base angles at 51 degrees 51 minutes. If you bisect this triangle and assign a value of 1 to each base, then the hypotenuse (the side opposite the right angle) equals phi (1.618..) and the perpendicular side equals the square root of phi. And that’s not all. A circle is drawn with it’s centre and diameter the same as the base of the large triangle. This represents the circumference of the earth. A square is then drawn to touch the outside of the earth circle. A second circle is then drawn around the first one, with its circumference equal to the perimeter of the square. (The squaring of the circle.) This new circle will actually pass exactly through the apex of the pyramid. And now the “wow”: A circle drawn with its centre at the apex of the pyramid and its radius just long enough to touch the earth circle, will have the circumference of the moon! Neat, huh! And the small triangle formed by the moon and the earth square will be a perfect 345 triangle (which doesn’t seem to mean much.)
** Source: http://geometry.wholesomebalance.com/Sacred_Geometry_2.html#Phi
Recommend this website to your friends:

|
|
|
|
Reply |
Message 2 of 35 on the subject |
|
Apocalipsis Capítulo 21
Vi un cielo nuevo y una tierra nueva; porque el primer cielo y la primera tierra pasaron, y el mar ya no existía más. 2 Y yo Juan vi la santa ciudad, la nueva Jerusalén, descender del cielo, de Dios, dispuesta como una esposa ataviada para su marido. 3 Y oí una gran voz del cielo que decía: He aquí el tabernáculo de Dios con los hombres, y él morará con ellos; y ellos serán su pueblo, y Dios mismo estará con ellos como su Dios. 4 Enjugará Dios toda lágrima de los ojos de ellos; y ya no habrá muerte, ni habrá más llanto, ni clamor, ni dolor; porque las primeras cosas pasaron.
5 Y el que estaba sentado en el trono dijo: He aquí, yo hago nuevas todas las cosas. Y me dijo: Escribe; porque estas palabras son fieles y verdaderas. 6 Y me dijo: Hecho está. Yo soy el Alfa y la Omega, el principio y el fin. Al que tuviere sed, yo le daré gratuitamente de la fuente del agua de la vida. (Aqui se esta haciendo REFERANCIA AL SALMO 119 QUE COMIENZAN Y FINALIZAN CON LAS LETRAS HEBREAS. AQUI ESTA EXPRESADO CON LAS GRIEGAS POR SU OBVIA ESCRITURA EN DICHO IDIOMA. EL AGUA DE LA VIDA TIENE FUERTE NEXO CON EL UNGIMIENTO DE BETANIA Y OSHANAH RABBAH)
¿PORQUE MARIA MAGDALENA UNGE LOS PIES DE JESUS EN
7 El que venciere heredará todas las cosas, y yo seré su Dios, y él será mi hijo.
8 Pero los cobardes e incrédulos, los abominables y homicidas, los fornicarios y hechiceros, los idólatras y todos los mentirosos tendrán su parte en el lago que arde con fuego y azufre, que es la muerte segunda.
Vino entonces a mí uno de los siete ángeles que tenían las siete copas llenas de las siete plagas postreras, y habló conmigo, diciendo: Ven acá, yo te mostraré la desposada, la esposa del Cordero. 10 Y me llevó en el Espíritu a un monte grande y alto, y me mostró la gran ciudad santa de Jerusalén, que descendía del cielo, de Dios, 11 teniendo la gloria de Dios. Y su fulgor era semejante al de una piedra preciosísima, como piedra de jaspe, diáfana como el cristal. (La gloria tiene un fuerte nexo sabatico segun EXODO 24)
12 Tenía un muro grande y alto con doce puertas; y en las puertas, doce ángeles, y nombres inscritos, que son los de las doce tribus de los hijos de Israel; 13 al oriente tres puertas; al norte tres puertas; al sur tres puertas; al occidente tres puertas. 14 Y el muro de la ciudad tenía doce cimientos, y sobre ellos los doce nombres de los doce apóstoles del Cordero.
15 El que hablaba conmigo tenía una caña de medir, de oro, para medir la ciudad, sus puertas y su muro. 16 La ciudad se halla establecida en cuadro, y su longitud es igual a su anchura; y él midió la ciudad con la caña, doce mil estadios; la longitud, la altura y la anchura de ella son iguales. (Efectivamente la GRAN PIRAMIDE ES LA CUBICACION DE UNA ESFERA)
17 Y midió su muro, ciento cuarenta y cuatro codos, de medida de hombre, la cual es de ángel. 18 El material de su muro era de jaspe; pero la ciudad era de oro puro, semejante al vidrio limpio; 19 y los cimientos del muro de la ciudad estaban adornados con toda piedra preciosa. El primer cimiento era jaspe; el segundo, zafiro; el tercero, ágata; el cuarto, esmeralda; 20 el quinto, ónice; el sexto, cornalina; el séptimo, crisólito; el octavo, berilo; el noveno, topacio; el décimo, crisopraso; el undécimo, jacinto; el duodécimo, amatista. 21 Las doce puertas eran doce perlas; cada una de las puertas era una perla. Y la calle de la ciudad era de oro puro, transparente como vidrio.
22 Y no vi en ella templo; porque el Señor Dios Todopoderoso es el templo de ella, y el Cordero. 23 La ciudad no tiene necesidad de sol ni de luna que brillen en ella; porque la gloria de Dios la ilumina, y el Cordero es su lumbrera. 24 Y las naciones que hubieren sido salvas andarán a la luz de ella; y los reyes de la tierra traerán su gloria y honor a ella. 25 Sus puertas nunca serán cerradas de día, pues allí no habrá noche. 26 Y llevarán la gloria y la honra de las naciones a ella. 27 No entrará en ella ninguna cosa inmunda, o que hace abominación y mentira, sino solamente los que están inscritos en el libro de la vida del Cordero.
Vamos con las medidas de la Gran Pirámide. Pongamos que aproximadamente la base mide 230,30 metros, que la altura original era de 146,6 y la apotema de sus caras (la línea que recorre todo el centro de la cara) es de 186,3. Pues bien, si simplificamos estas medidas y consideramos que la base mide 2, la altura mediría 1,272 y la apotema sería 1,618. Es decir, un triángulo que tenga como base 2, como altura 1,272 y como los lados 1,618, tendría las mismas proporciones que la Gran Pirámide en su corte transversal. La altura divide a ese triángulo en dos triángulos rectángulos menores que tendrían como base 1, como altura 1,272 y como hipotenusa 1,618.
O sea, que la Gran Pirámide está edificada teniendo como armazón a un triángulo rectángulo que tiene como base la unidad de medida, como altura la raíz del número Fi (1,618). Por lo que queda demostrado que el número Fi está incorporado a la Gran Pirámide sin distorsionar ninguna medida. Por si acaso hubiera dudas, la secante del ángulo de 51 grados y 51 minutos (ángulo de inclinación de la Gran Pirámide) es 1,618 (Fi) y por ende el coseno de 51 grados y 51 minutos es el inverso de Fi (0,618).
Las medidas de la Gran Pirámide resuelven la cuadratura de la circunferencia. Demostración: La circunferencia que tiene como radio la altura de la pirámide tiene la misma longitud que la base cuadrada de la Gran Pirámide.
Radio = 146,6 x 2Pi = 921
Lado de Base = 230,30 x 4 = 921
Lo cual implica que si dividimos la base de la pirámide por el doble de la altura obtenemos el número Pi.
Las medidas de la Gran Pirámide resuelven la cuadratura del círculo. Demostración: un rectángulo formado por la base de la Gran Pirámide y su altura tiene la misma superficie que un semicírculo que tenga como radio la altura de la pirámide.
Superficie del semicírculo = Pi x radio2 /2 = 33.758
Superficie del rectángulo = 230,3 x 146,6 = 33.761
Las medidas de la Gran Pirámide resuelven la cubicación de la esfera. Demostración: según la geometría, la mitad de un círculo plano es también matemática y rigurosamente igual en área a la superficie esférica de un cuadrante de 90 grados. O sea, que un rectángulo cuya altura y base sean las de la pirámide tiene la misma superficie que un cuadrante esférico cuya altura sea la de la pirámide y su arco la base de la Gran Pirámide.
Superficie del cuadrante esférico = arco x radio = 230,3 x 146,6 = 33.761
Superficie del rectángulo = 230,3 x 146,6 = 33.761.
Otra demostración: la superficie del prisma generado tomando la base y la altura de las caras de la Gran Pirámide (una caja donde se pudiera meter la Gran Pirámide) tiene la misma superficie que la semiesfera generada tomando como radio la altura de la Gran Pirámide.
Base x altura 230,3 x 146,6 x 4 caras = 135.047
Superficie de la semiesfera = 4 x Pi R2 / 2 = 4 x Pi x 146,6 x 146,6 /2 = 135.035.
Ahora nos enfrentamos a un problema con dos posibles soluciones:
1. Los constructores de la Gran Pirámide adquirieron en tiempos de Keops el conocimiento de los números Pi y Fi e inmediatamente después se olvidó en Egipto tal conocimiento, en una absoluta pérdida de memoria sin parangón conocido en la historia de la ciencia.
2. Los egipcios, que desconocían estas proporciones, no pudieron construir ni siquiera el boceto arquitectónico de la Gran Pirámide. Pero esa es otra historia.
|
|
|
|
Reply |
Message 3 of 35 on the subject |
|
¿Quién y cómo construyeron las pirámides?
La fascinación que despierta un monumento tan antiguo y singular como la Gran Pirámide de Keops ha dado lugar a las más diversas interpretaciones fuera del estricto ámbito de la arqueología. Unos piensan que se trata de una gigantesca biblia de piedra, cuyos elementos arquitectónicos esconderían, codificados, arcanas revelaciones de carácter iniciático. Otros creen que fue construida con ayuda de tecnología extraterrestre y que estaba destinada a servir, en esos tiempos remotos, de punto de referencia para el aterrizaje de potentes naves interestelares.
También hay quienes atribuyen a su forma geométrica el poder de concentrar la energía cósmica, lo que, entre otras cosas, valdría para preservar incorrupto el cadáver del faraón, depositado justo en el centro de la construcción. Finalmente otra hipótesis de tipo esoterista asegura que la Gran Pirámide es en realidad un mayúsculo calendario universal, donde, por la disposición de pasadizos y cámaras, podría leerse el pasado y el futuro de toda la humanidad. Las celebres pirámides de Egipto llamadas de Keops, Kefrén y Micerinos, situadas en el límite sudoeste de El Cairo. La mayor de las tres, la de Keops (la Gran Pirámide) simbolizaba la Fuerza de la Naturaleza; la segunda, a un tiro de flecha de la primera, expresaba el movimiento, y la tercera, a menos de un tiro de piedra de ésta, era símbolo del Tiempo, de la Eternidad. Parece que hace tres mil años, la base de estas pirámides estaban orientadas de modo que una de sus caras miraba al norte, la segunda al oriente (dominio del Alfa) y la tercera al occidente (símbolo del Omega). Y que una de las cúspides del triángulo de base, orientada hacia el sur, señalaba el reino de las tinieblas.
Ante una obra humana de semejante calibre, tan grande y tan absolutamente resistente al paso del tiempo, continúa siendo inevitable preguntarse (al igual que hiciera Herodoto y luego Napoleón) cómo fueron levantadas las pirámides, y sobre todo, por qué. Y es que el inmenso esfuerzo que supuso extraer, transportar, tallar y encajar cada uno de los bloques no hubiese sido posible sin una fuerza espiritual que impulsase los músculos y la voluntad de los trabajadores en la erección de esta magna construcción, la más imponente de toda la historia de la humanidad.
Muchos son los cálculos y cifras barajados por los especialistas acerca de las pirámides de la IV dinastía. Durante los cien años de historia egipcia que corresponden al periodo de su construcción, se tuvo que colocar un bloque de piedra cada cuatro minutos y medio, con un promedio de 2500 kilos por bloque. En total, 8.972.500 metros cúbicos y 12.000.000 de bloques manipulados entre 25.000 personas trabajando una jornada de 10 horas diarias. Lo que era imposible con la tecnología de la Edad de Piedra. La más convincente de las teorías es una rampa que giraba en espiral alrededor de la pirámide. Los bloques se remolcaban sobre los trineos hasta el punto más alto, pero construir esta rampa sería más difícil que construir la pirámide. Todavía sigue siendo un misterio como lograron determinar la planta de la Gran Pirámide de Keops con tanta exactitud. Según los cálculos modernos, los ángulos entre cada dos lados de la base miden 89 grados, 59 minutos, 5 segundos; y 90 grados, 0 minutos y 58 segundos respectivamente. Tamaña precisión en la búsqueda del ángulo recto permitió que los cuatro lados fueran absolutamente iguales, o casi. En realidad tienen una desviación máxima de 5 centímetros, sobre una longitud total de 230 metros por lado. Nadie sabe cómo fueron extraídas las piedras de las canteras para la construcción de estas pirámides. Dice una extraña leyenda árabe que, para construir la Gran Pirámide, se colocaban bajo las piedras unas hojas de papiro en las que había escritos mensajes secretos. Tras ser golpeadas por una varita, las piedras iban ascendiendo por el aire hasta situarse cada una en su lugar.
Hay un informe, cuya autenticidad no se podría asegurar, según el cual en 1978 Israel lanzó un ataque de comandos en gran escala para capturar un OVNI que se encontró enterrado bajo una de las grandes pirámides de Egipto. Si es cierto, sería una prueba contundente de una civilización avanzadísima y de la conexión entre los constructores de las pirámides y los platillos volantes.
La Gran Pirámide
Por: Manuel José Delgado
¿Es la tumba de Keops?
Para algunos, esta construcción fue un monumento funerario. Para otros, un templo. No faltan quienes afirman que es el compendio de un conocimiento muy avanzado y desarrollado por una civilización desaparecida, o por extraterrestres venidos de lejanas estrellas. Tal vez ninguno, o todos en parte, tengan razón, ya que la Gran Pirámide, testigo mudo de más de cinco millones de amaneceres, ha visto cómo su estructura ha servido de escenario para que diversos arquitectos, en distintas épocas, oculten cámaras secretas, algunas de ellas todavía no descubiertas.
Hoy, como siempre, el mundo mira a la Gran Pirámide con la esperanza de que se desvelen sus misterios. Mañana, el mes que viene o el próximo año, saltará a la prensa el descubrimiento de nuevas cámaras, a medida que los arqueólogos quieran confirmar o desmentir las numerosas teorías que se han elaborado en torno a este coloso de piedra.
Estas son las paradojas que nos intrigan de la única maravilla del mundo antiguo que se conserva. Para muchos estudiosos, resuena con ecos de misterio, múltiples y solemnes preguntas sin respuesta, recuerdos de una cultura que empleó una ciencia tan asombrosa como anacrónica para expresarse. Para otros fue un monumento erigido a la vanidad, sin más ciencia que la fuerza bruta aportada por miles de hombres. Desde esta última posición se tacha invariablemente de "casualidad" todos los datos aportados por sus medidas que sugieren que en este monumento se codificaron conocimientos técnicos especialmente precisos de medidas fundamentales de nuestro planeta.
Pese a que las obras, referencias y artículos que tratan el tema de las pirámides se cuentan por cientos de miles, los libros de texto escolares y universitarios zanjan el tema en dos lacónicas frases que se centran en sendas aseveraciones: las pirámides son tumbas y la Gran Pirámide fue construida por Keops.
Los egiptólogos llegaron a aceptar esta teoría únicamente sobre la base de los datos proporcionados por dos viajeros que nada tenían que ver con la arqueología. Pero estas pruebas, aportadas respectivamente por el historiador griego Herodoto de Helicarnaso en el siglo V a.C. y por el coronel inglés Richard Howard-Vyse en 1837, como veremos, nada tienen de científicas, aparte de que han sido manipuladas e intoxicadas, tanto en sus propios orígenes como en sus adaptaciones posteriores, en un intento desesperado de presentarlas como auténticas y concluyentes.
Para la arqueología oficial el cartucho del faraón Keops, encontrado en la quinta Cámara de Descarga, es la más clara evidencia de que la Gran Pirámide fue construida por él durante la IV Dinastía del Imperio Antiguo, en la primera mitad del III Milenio a.C. Asimismo, las referencias de Herodoto en su obra 'Los Nueve Libros de Historia' son consideradas como un respaldo documental suficiente para atribuir a Keops la autoría de la obra. Es la idea aceptada y generalizada para todos aquellos que no han realizado las mínimas comprobaciones, porque a poco que se revise la historia vemos que tales argumentos carecen absolutamente de fundamento.
Las pruebas del Coronel Vyse
En 1835 llegó a la meseta de Giza el coronel Howard-Vyse. Su principal interés se centraba en poder demostrar a su ilustre familia que era merecedor de su apellido tras haber llevado una vida poco recomendable. Su carrera militar en el ejército británico de la India había pasado sin pena ni gloria, por lo que centró su atención en intentar pasar a la Historia como el promotor de un gran descubrimiento, en una época en la que numerosos investigadores sacaban a la luz los restos de la cultura faraónica y ésta era moda culta en Europa.
Por aquellos días la zona estaba siendo excavada por el italiano Giovanni Battista Caviglia, un capitán de navío que decidió dedicar su vida a un estudio meticuloso de la Gran Pirámide. Éste ya había conseguido despejar y limpiar el camino, cubierto por toneladas de escombros y de excrementos de murciélagos; tanto del pasaje descubierto en 1765 por Nathaniel Davidson, que iba hasta la primera Cámara de Descarga, como del denominado Pozo, que recorre la pirámide desde la Gran Galería hasta el canal descendente, cerca de la Cámara del Caos. Howard-Vyse le ofreció financiación a cambio de poder presentarse a la prensa como copartícipe de los hallazgos que se produjesen, propuesta que Caviglia rechazó, ya que vio en el coronel cierto ánimo de protagonismo en lugar del espíritu de estudio que debía presidir toda investigación arqueológica. La meticulosidad y ciencia arqueológica aplicada por Caviglia en sus excavaciones fueron refrendadas posteriormente por la arqueología. Sus trabajadores aprendieron su método de trabajo y el propio William M. Flinders Petrie, el mejor arqueólogo y metrólogo que ha trabajado en la Gran Pirámide, cuando llegó a Egipto en 1880, buscó y contrató a Ali Gabri, quien 40 años antes fue capataz de Caviglia.
Ante la negativa de asociación, el coronel Vyse consiguió obtener o, mejor dicho, comprar al gobierno egipcio un "firman", es decir, un permiso para excavar en Giza. Con unos recursos financieros notables, que entonces ascendieron a diez mil libras, organizó todo un pelotón de trabajadores. De verdad estaba dispuesto a aparecer en los periódicos ingleses como el autor de un hallazgo importante. Contrató entonces como capataz de los trabajos a Caviglia, pero el método empleado por éste resultaba lento para sus aspiraciones de gloria, por lo que decidió despedirle tras una larga serie de discusiones. Contrató entonces los servicios del ingeniero John Perring para iniciar su particular búsqueda desenfrenada de un descubrimiento importante, aunque para ello utilizara métodos tan destructivos como la pólvora. Tras volar el hombro y el lomo de la esfinge centró sus explosiones en el interior de la Gran Pirámide, ya que las prospecciones que intentó realizar en el nicho de la Cámara de la Reina o en el suelo de la Cámara del Rey se realizaban de forma lenta y costosa.
La idea de que sobre la Cámara de Descarga descubierta por Davidson había otras similares era de Caviglia, refrendado por una pequeña grieta por la que se podía introducir un palo, pero la composición granítica de los bloques hacía difícil su perforación. Howard-Vyse decidió usar también aquí la pólvora para abrirse camino hacia arriba y encargó el trabajo a un operario llamado Daued, hombre que vivía exclusivamente del hachís y del alcohol y cuya inteligencia no debía ponerle demasiados reparos para jugarse la vida al provocar una explosión acurrucado tras algún pequeño nicho. El estallido debió resonar con enorme fuerza y toda la pirámide se llenó de polvo, pero el resultado fue que consiguieron abrir un agujero lo suficientemente grande como para pasar a otra estancia superior. De la misma forma, y tras numerosas voladuras se consiguieron abrir camino hacia la parte superior del monumento, hasta alcanzar la quinta Cámara de Descarga, dejando por fin a la pirámide con la estructura interior que ahora conocemos.
Pero lo importante es que, pese a que estas cámaras se encontraron vacías de mobiliario y ornamentos, Howard-Vyse presentó al mundo su descubrimiento de pinturas y textos jeroglíficos. Fueron estudiados por Samuel Birch, experto en jeroglíficos del Museo Británico, quien atribuyó uno de los cartuchos encontrados a Keops, el mismo faraón que citara Herodoto, y la arqueología respiró satisfecha por tener la prueba irrefutable que le permitía identificar al constructor de la Gran Pirámide de Giza. El Coronel regresó a Inglaterra, donde llegó rodeado de grandes honores, aunque en su travesía se hundió su barco frente a las costas de Cartagena con gran cantidad de restos arqueológicos a bordo, entre ellos el sarcófago recuperado de la pirámide de Micerinos. Howard-Vyse fue posteriormente nombrado General del Ejército Británico.
Sin embargo, el descubrimiento de la escritura jeroglífica en las Cámaras de Descarga de la Gran Pirámide estuvo rodeado de acciones sospechosas por parte de sus protagonistas. Howard-Vyse nunca permitió a Caviglia acceder al descubrimiento y el capataz de los trabajos fue despedido. Los ingenieros de su equipo, Mash y Perring, sí que pudieron contemplar el hallazgo y Perring, en su libro titulado 'Las Pirámides de Giza a la luz de su exploración verdadera y de las medidas tomadas allí mismo', refiere cómo se fijaron en las llamadas líneas de albañil (trazos de pintura roja), aunque en un principio no se fijaron en los jeroglíficos, que descubrieron "posteriormente" en una inspección más detallada.
Tras la apertura con pólvora del acceso a las cámaras, Vyse no permitió la entrada de nadie salvo la de un amigo suyo llamado J. R. Hill, empleado de una fábrica local de cobre. Curiosamente, cuando el coronel se retiró de Egipto, Hill se convirtió en el propietario de El Cairo Hotel, algo que no se explica con el salario de un simple operario. Es de suponer que la amistad y la colaboración entre ambos le proporcionó el dinero suficiente para tal adquisición y su complicidad se vio refrendada por el público agradecimiento a Hill que Vyse hizo en su libro 'Operaciones llevadas a cabo en la Pirámide de Gizeh en 1837'. Hill tenía acceso libre a las cámaras, a las que subía para pintar los nombres con las que las bautizaron, y no dejaba que nadie más le acompañase en su empresa. La palabra fraude comenzó a flotar en la atmósfera de Giza, descubriéndose posteriormente la más burda falsificación que conoce la historia.
La copia que recibió el doctor Samuel Birch de los cartuchos y jeroglíficos encontrados en las Cámaras de Descarga descubiertas por Vyse le dejaron perplejo. Si bien pudo reconocer el nombre de Keops (khufú), tanto en los otros cartuchos como en la propia escritura que los acompañaban, existían elementos ciertamente anómalos. En primer lugar, los signos no se parecían a la escritura jeroglífica del Imperio Antiguo, sino más bien a otra escritura cursiva conocida como demótico, que se desarrolló en Egipto mucho más tarde. Asimismo, varios signos jeroglíficos eran del todo desconocidos y, algo inaudito, algunos de los signos conocidos estaban al revés. Algo también desconcertante fue la aparición de un cartucho con el nombre de un faraón desconocido, Khnum-khuf, que algunos egiptólogos han intentado asimilar a alguna variante del propio Khufú o Keops.
Afortunadamente, el fraude del coronel Howard-Vyse se pudo comprobar definitivamente cuando se investigaron las fuentes egiptológicas que usó en su estancia en Egipto y se pudieron reconstruir sus andanzas delictivas. La piedra Rosetta fue descubierta en 1799 y el conocimiento que se tenía de los jeroglíficos en el decenio de 1830 todavía era mínimo. El único texto que Hill pudo haber consultado era 'Materia Hieroglyphica', de Sir John Wilkinson, en el que aparecían los errores de transcripción del nombre de Keops de la misma forma en que aparecieron escritos en las dos primeras cámaras descubiertas por Vyse. Justo cuando descubrieron la cuarta Cámara de Descarga, los impostores se enteraron de una nueva versión del diccionario de Wilkinson, titulado 'Hábitos y costumbres del Antiguo Egipto', y tras correr a El Cairo para adquirirlo comprobaron que el autor había cambiado de opinión sobre la forma de escribir la palabra Keops, por lo que se dieron cuenta de que habían escrito mal el nombre. Este error fue rectificado en las dos últimas cámaras, donde aparece la grafía correcta con el nombre de Khufú o Jufú pero, nuevamente, con otros dos errores de envergadura.
Wilkinson, pese haber rectificado la grafía de Khufú, volvía a cometer un error al interpretar el círculo que correspondía a letra Kh de Khufú. Hoy en día se sabe que ese signo corresponde al llamado "tamiz" o "cedazo" que se corresponde con un círculo con varias líneas que lo cruzan. Pues bien, el error de Wilkinson, y curiosamente también el error del cartucho de Keops, no en la quinta cámara sino en las cámaras anteriores, es confundirlo con el símbolo del sol, de Ra, que equivale a un círculo con un punto en el centro, por lo que Vyse y Hill falsificaron el nombre del faraón escribiendo la palabra Raufú en lugar de Khufú. Además, los signos jeroglíficos dibujados no guardan la postura que debieran tener, ya que la representación correcta sería la que viésemos de ese mismo cartucho reflejada en un espejo, algo inaudito para un escriba de tiempos de Keops.
¿Cómo es posible que tamaña chapuza haya prevalecido en la egiptología como la prueba incuestionable de la identidad del constructor de la Gran Pirámide? Posiblemente, porque si no la construyó Keops aparece una laguna histórica de tal envergadura que sería por sí sola capaz de cuestionar todas nuestras ideas sobre la historia antigua. Si el monumento perteneciera a un tiempo anterior al Imperio Antiguo, nos situaríamos de lleno, como mínimo, en el IV Milenio a.C., y según el consenso de los historiadores, rozando el Neolítico. En este caso, habría que retrotraer la fabulosa construcción a los tiempos predinásticos y a sus legendarias fuentes, que hablan de un país gobernado por dioses y semidioses. Una época en la cual la realidad y el mito se confunden peligrosamente para los fundamentos que nuestra cultura racionalista ha dado a la Historia. Si ya parece cosa de locos atribuir este monumento a gentes que no conocían la rueda ni el hierro, parece excesivo pedirle a la ciencia oficial que al menos examine ecuánimemente la posibilidad de que esas leyendas referidas a dioses y semidioses se encuentre más cerca a lo que realmente ocurrió que a la mitología.
Sin embargo, más que sospechosamente, de las cinco Cámaras de Descarga de la Gran Pirámide sólo las cuatro descubiertas por el coronel Vyse tienen escritura, ya que la primera, la descubierta por Davidson, se encuentra vacía de todo signo. Además, aparte de los cartuchos falsificados por Vyse no existe tampoco ningún otro dibujo o jeroglífico que adorne las paredes interiores de la Gran Pirámide y, por tanto, ninguna referencia que indique quién fue su constructor y cuándo se proyectó y realizó el monumento.
Tal vez, por esta razón todos aquellos crédulos que, por conveniencia o carencia de sentido crítico, no han visto ninguna sombra de duda en el presunto descubrimiento del coronel Vyse, se muestran escépticos a la hora de valorar otros documentos que sugieren con fuerza que la Gran Pirámide ya estaba construida en tiempos de Keops. Así, por ejemplo, la denominada Estela del Inventario, conservada en el Museo de El Cairo, relata cómo Keops fundó una orden de culto a la diosa Isis, "Señora de la Pirámide". Este elemento supondría que ya existía en tiempos de la IV Dinastía del Imperio Antiguo y entonces servía como templo de la diosa.
Las pruebas de Herodoto
Herodoto de Helicarnaso, el denominado "Padre de la Historia", atribuyó la construcción de la primera pirámide de Giza a Keops, la segunda a Kefrén y la tercera a Micerinos, nombres helenizados que la arqueología ha identificado como correspondientes a los faraones Khufú, Khafra y Menkaura. Herodoto ha sido tachado de superficial y sus afirmaciones, aparte de la cita de los faraones mencionados, no son tenidas en cuenta a la hora de avalar hechos fidedignos. De todas formas, hay que considerar que el periodismo o la investigación histórica tal como hoy la conocemos dista mucho de los trabajos realizados por los autores clásicos. Los guías que le acompañaron, y las gentes a las que pudo consultar, le contaron su parecer y así lo reflejó en su obra 'Los Nueve Libros de la Historia'. Pero él mismo reconoce puntualmente en su segundo libro, dedicado a Euterpe, en el capítulo CXXIII, en qué contexto deben ser evaluadas sus crónicas: "...si alguno hubiere a quien se hagan creíbles esas fábulas egipcias, sea enhorabuena, pues no salgo fiador de lo que cuento, y sólo me propuse por lo general escribir lo que otros me referían...".
Yo estoy convencido de que Herodoto no elucubraba, que reflejaba sin malicia lo que su memoria recordaba de todo aquello que le contaron: "...Hasta el reinado de Rampsinito, según los sacerdotes, viose florecer en Egipto la justicia, permaneciendo las leyes en su vigor y viviendo la nación en el seno de la abundancia y prosperidad; pero Keops, que le sucedió en el trono, echó a perder un Estado tan floreciente. Primeramente, cerrando los templos, prohibió a los egipcios sus acostumbrados sacrificios; ordenó después que todos trabajasen por cuenta del público...".
Pero si hacemos caso de la información dada en la Estela del Inventario, la Gran Pirámide era un monumento antiguo dedicado a la diosa Isis. Si Keops decidió hacerse allí su tumba y después ordenó cerrar la pirámide, entendemos el por qué de las frases de Herodoto y la razón principal para que Keops fuese considerado un tirano: "... Viéndose ya falto de dinero, llegó Keops a tal extremo de avaricia y bajeza, que en público lupanar prostituyó a una hija, con orden de exigir en recompensa de su torpe y vil entrega cierta suma... pidiendo a sus amantes que le costearan cada uno una piedra para su edificio".
De las frases anteriores sólo se puede sacar en claro el odio que a Keops se tenía, pues son inconcebibles tales informaciones. Sin embargo, en otros textos sí que podemos sacar conclusiones más coherentes referidas a la Gran Pirámide: "En esta fatiga ocupaba de continuo hasta 3.000 hombres, a los cuales de tres en tres meses iban relevando, y sólo en construir el camino para conducir dicha piedra de sillería hizo penar y afanar a su pueblo durante diez años enteros, lo que no debe extrañar, pues este camino, si no me engaño, es obra poco o nada inferior a la pirámide misma... y en los diez años de fatiga empleados en la construcción del camino, no se incluye el tiempo invertido en preparar el terreno del collado donde las pirámides debían levantarse, y en construir una cámara subterránea que sirviese para sepulcro real, situada en una isla formada por una acequia que del Nilo se deriva. En cuanto a la pirámide se gastaron en su construcción veinte años". |
|
|
|
Reply |
Message 4 of 35 on the subject |
|
La geometría sagrada
La opinión unánime de todos los arquitectos e ingenieros que han estudiado la Gran Pirámide es que su construcción obedece a un replanteo. Es decir, de los planos de dibujo se pasó a la edificación, eliminando cualquier teoría que pretenda indicar que se pusieron a subir bloques de manera arbitraria. Esos planos fueron concebidos siguiendo los conceptos que el arquitecto quiso incorporar y la función de la piramidología consiste precisamente en adivinar dichos planteamientos, ya que las medidas de la Gran Pirámide fueron proyectadas bajo un criterio arquitectónico, como cualquier edificio actual. Los arquitectos, tras realizar los estudios pertinentes, pueden llegar a averiguar cuáles fueron esos planteamientos. Otra cosa es jugar con los números para hallar un carnet de identidad, un número de teléfono o cualquier otro malabarismo intelectual. La ciencia es otra cosa.
Vamos con las medidas de la Gran Pirámide. Pongamos que aproximadamente la base mide 230,30 metros, que la altura original era de 146,6 y la apotema de sus caras (la línea que recorre todo el centro de la cara) es de 186,3. Pues bien, si simplificamos estas medidas y consideramos que la base mide 2, la altura mediría 1,272 y la apotema sería 1,618. Es decir, un triángulo que tenga como base 2, como altura 1,272 y como los lados 1,618, tendría las mismas proporciones que la Gran Pirámide en su corte transversal. La altura divide a ese triángulo en dos triángulos rectángulos menores que tendrían como base 1, como altura 1,272 y como hipotenusa 1,618.
O sea, que la Gran Pirámide está edificada teniendo como armazón a un triángulo rectángulo que tiene como base la unidad de medida, como altura la raíz del número Fi (1,618). Por lo que queda demostrado que el número Fi está incorporado a la Gran Pirámide sin distorsionar ninguna medida. Por si acaso hubiera dudas, la secante del ángulo de 51 grados y 51 minutos (ángulo de inclinación de la Gran Pirámide) es 1,618 (Fi) y por ende el coseno de 51 grados y 51 minutos es el inverso de Fi (0,618).
Las medidas de la Gran Pirámide resuelven la cuadratura de la circunferencia. Demostración: La circunferencia que tiene como radio la altura de la pirámide tiene la misma longitud que la base cuadrada de la Gran Pirámide.
Radio = 146,6 x 2Pi = 921
Lado de Base = 230,30 x 4 = 921
Lo cual implica que si dividimos la base de la pirámide por el doble de la altura obtenemos el número Pi.
Las medidas de la Gran Pirámide resuelven la cuadratura del círculo. Demostración: un rectángulo formado por la base de la Gran Pirámide y su altura tiene la misma superficie que un semicírculo que tenga como radio la altura de la pirámide.
Superficie del semicírculo = Pi x radio2 /2 = 33.758
Superficie del rectángulo = 230,3 x 146,6 = 33.761
Las medidas de la Gran Pirámide resuelven la cubicación de la esfera. Demostración: según la geometría, la mitad de un círculo plano es también matemática y rigurosamente igual en área a la superficie esférica de un cuadrante de 90 grados. O sea, que un rectángulo cuya altura y base sean las de la pirámide tiene la misma superficie que un cuadrante esférico cuya altura sea la de la pirámide y su arco la base de la Gran Pirámide.
Superficie del cuadrante esférico = arco x radio = 230,3 x 146,6 = 33.761
Superficie del rectángulo = 230,3 x 146,6 = 33.761.
Otra demostración: la superficie del prisma generado tomando la base y la altura de las caras de la Gran Pirámide (una caja donde se pudiera meter la Gran Pirámide) tiene la misma superficie que la semiesfera generada tomando como radio la altura de la Gran Pirámide.
Base x altura 230,3 x 146,6 x 4 caras = 135.047
Superficie de la semiesfera = 4 x Pi R2 / 2 = 4 x Pi x 146,6 x 146,6 /2 = 135.035.
Ahora nos enfrentamos a un problema con dos posibles soluciones:
1. Los constructores de la Gran Pirámide adquirieron en tiempos de Keops el conocimiento de los números Pi y Fi e inmediatamente después se olvidó en Egipto tal conocimiento, en una absoluta pérdida de memoria sin parangón conocido en la historia de la ciencia.
2. Los egipcios, que desconocían estas proporciones, no pudieron construir ni siquiera el boceto arquitectónico de la Gran Pirámide. Pero esa es otra historia.
Los constructores ocultos
Desde la más remota antigüedad todos los hombres de ciencia miraron a la Gran Pirámide como poseedora de informaciones referentes a las medidas terrestres y celestes. Y, posiblemente, tales datos se hallen incorporados en sus proporciones.
Pero hay más. El premio nobel Linus Pawling demostró que la molécula de agua no es H2O, sino un polímero formado por 5H2O. El eminente científico afirmó asimismo que la forma de la molécula del agua corresponde a una pirámide de base cuadrada, en cuyas cinco esquinas se situaría un H2O, y que el ángulo de esta formación era 52º.
Con este dato podemos afirmar que la Gran Pirámide es el mayor monumento construido a la molécula del agua. Pero, curiosamente, el único mineral cuya cristalografía corresponde exactamente a la geometría de la pirámide es el diamante, el carbono puro, con lo que tenemos que el agua y el carbono, los principales elementos que componen el cuerpo humano se hallan representados en este singular monumento. Quizás sea casualidad, pero el número de hiladas de la pirámide corresponde al número de huesos que tiene el ser humano, 204. Y podría seguir enumerando "casualidades" que indican que, por un lado, la Gran Pirámide es el mayor compendio astronómico escrito en piedra pero, por otro lado, representa al ser humano en toda su extensión, física y espiritual.
Quizás sea por ello que en el interior de la Gran Pirámide nos sentimos afectados. Su geometría sagrada influye en los organismos y provoca una energía sutil capaz de alterar los instrumentos electrónicos de medida. Algunos consideran que la Gran Pirámide actúa como una antena emisora-receptora de sensaciones e informaciones.
Quién sabe. No existen pruebas categóricas para responder a la pregunta de quiénes fueron esos seres superiores que edificaron la Gran Pirámide. Lo que sí sabemos es que la tecnología y los conocimientos empleados en su construcción no estuvieron al alcance de los egipcios de la IV Dinastía. O, por lo menos, que no deberíamos clasificar tan superficialmente un monumento que se ríe del tiempo y de todos los que aventuramos nuestras temblorosas hipótesis porque, en este momento, no sabe más sobre la Gran Pirámide el que más respuestas aporta, sino el que más preguntas se hace.
Una clave de cara al visitante
La Gran Pirámide parece empeñarse en mantener ocultos todos sus secretos, pero aunque los arqueólogos ortodoxos no le presten ningún valor, si existe en ella un testimonio escrito. El grabado al que nos referimos se encuentra situado en la puerta original de Keops, rodeado por el gigantesco dintel que marca la entrada al monumento. Está formado por cuatro letras que son, de izquierda a derecha, una V, un circulo partido por una línea transversal, tres rayas horizontales en paralelo, y por último, otro círculo partido por dos líneas verticales.
Mucho se ha especulado sobre el autor de estos cuatro signos, y las teorías van desde que sea simplemente una broma, hasta que sea una señal de habitantes de otro planeta. Toda esta controversia no es de extrañar, ya que en Egipto no existen símbolos similares a los que podemos observar en este famoso tetragrama.
Hace ya algunos años varios estudiosos descubrieron que las letras pertenecían a ancestrales alfabetos libios. Se sacaron las valencias correspondientes de éstas, pero para su traducción se empleó el copto, que nada tiene que ver con el sahariano antiguo (alfabeto en el que está escrito el tetragrama).
El sahariano antiguo es un alfabeto que se creó, según las teorías ofíciales, hacia el 2000 a. C., pero recientes descubrimientos sitúan su nacimiento hace 6.000 años en la zona de Tassili, al sur-oeste de Argelia, lo que lo convierte en la primera escritura de la Humanidad. Ello permite formular la hipótesis de que el tetragrama de la Gran Pirámide sea original a su construcción, convirtiéndose de esa forma en el único mensaje escrito que posee la última maravilla del mundo antiguo. Aún así, y sin descartar que se trate de una simple coincidencia, habría, además, que suponer que tal inscripción se grabó apresurada y subrepticiamente, porque su tosca factura nada tiene que ver con el perfecto acabado, a veces sorprendente por su regularidad y precisión, del que hicieron gala los antiguos egipcios en sus trabajos. Lo más lógico es deducir que alguien conocedor de la arcaica escritura sahariana, grabó hace siglos el célebre tetragrama cuando la pirámide ya carecía de las losas de revestimiento.
Las valencias de la inscripción, de izquierda a derecha, son las letras D, B, Q, y B. Éstas forman dos palabras cuya raíz es DB y QB; los fonemas que se obtienen tras esta operación son dabba iqbut. La primera de las palabras significa "cuidar", o la expresión coloquial "tomarse las cosas como vengan". La segunda palabra, iqbut, si es esclarecedora, ya que su significado literal seria "cúpula que recubre la tumba de un hombre santo". Para comprender el verdadero sentido de estas palabras debemos entender que los equivalentes del diccionario antes mencionado, están hoy en día aislados, ya que la actual religión berebere es la mahometana. Si extrapolarnos su significado a hace miles de años, podemos obtener la conclusión de que alguien semi divino, o al menos adorado como tal, fue enterrado en la Gran Pirámide. Tal consideración es aplicable al propio faraón,presuntarnente sepultado en el colosal monumento. Pero también podría hacer referencia a un ser distinto, lo que nos llevaría de nuevo a la posible existencia de estancias aún no descubiertas, y el texto tendría el carácter de un mensaje dejado para la posteridad por alguien conocedor de ese secreto celosamente guardado por los constructores. Una especulación novelesca sin duda, pero no despreciable en un edificio tan singular y cargado de misterio.
+ Aquí tienes un interesante video en Real Player sobre las Pirámides. Podrás verlas como si las estuvieras visitando en un viaje guiado.
- Modem de 56K - Duración del video: 4. 7 minutos - Tiempo de descarga: aprox. 6 minutos.
El legado de los dioses
La teoría extraterrestre cuenta, en el caso de Egipto, con todo género de indicios. Simplicio dijo que los habitantes de este país conservaban observaciones astronómicas de los últimos 600.000 años. Diógenes Laercio databa la antigüedad de los cálculos astronómicos egipcios en unos 48.000 años y Marciano Capella decía que estudiaron las estrellas durante 40.000 años. Pero, por supuesto, los historiadores y egiptólogos oficiales no aceptan esto, como tampoco las cronologías que remontan las lista de sus míticos regentes predinásticos a aquella remota época.
La representación más espectacular del firmamento egipcio está en el techo de una capilla del templo de Hathor. Se trata del famoso Zodiaco circular de Dendera. El notable egiptólogo y hermetista R. A. Schwaller de Lubicz demostró que en este zodiaco se encuentran las pruebas de la antigüedad del santuario. Consiste en dos círculos de constelaciones, toscamente superpuestos, centrado uno en el Polo Norte geográfico y otro en el real, el de la eclíptica, hacia el que señalaría el eje de la Tierra si no oscilase. El diámetro del zodiaco de oriente a occidente cruza la constelación de Piscis, evidenciando que se construyó en la era regida por esta constelación, hace más o menos 2.100 años. Pero un par de jeroglíficos, en su borde, insinúan la presencia de otro eje que pasa por el comienzo de la era de Tauro, suceso ocurrido ¡más de cuarenta siglos antes!
Ello indica que los egipcios conocían la precesión de los equinoccios (movimiento de los puntos equinocciales en virtud del cual se anticipan un poco, de año en año, las épocas de los equinoccios) y que la tradición religiosa mantenida en el templo de Dendera data de ¡cuatro mil años antes de lo que hasta ahora se ha aceptado!
EL ÍNDICE GEODÉSICO
Pero la hipótesis de visitas extraterrestres en el pasado que habrían contribuido al conocimiento de la astronomía adquiere un especial relieve cuando nos enfrentamos a la Gran Pirámide. Pasando por alto las numerosas referencias egipcias a sus "dioses instructores", que merecerían un desarrollo aparte, los datos suministrados por las medidas de este monumento despejan cualquier duda en lo que concierne a un conocimiento astronómico y geodésico absolutamente anacrónico para el que los egiptólogos otorgan a los primitivos moradores de las riberas del Nilo. Sencillamente, la tecnología de que disponían era claramente insuficiente para la obtención de tales datos.
Según los egiptólogos, las primeras tumbas faraónicas conocidas son las de la XI dinastía, es decir, que datan de 2.160 a 2.000 años a.C. Están situadas frente a Karnak, en la llanura de El Taraf, al nordeste del Valle de los Reyes y se abren hacia el oeste, es decir, hacia el Sol poniente. En consecuencia, las pirámides orientadas al norte no eran sepulturas, sino templos y, como tales, contenían no sólo la cultura religiosa sino un conocimiento, adquirido de los dioses, que se plasmó en forma de datos que relacionaban el monumento con las medidas geodésicas de nuestro planeta. Han sido muchos los investigadores que han comprobado la precisión de estos datos.
Jomard, que participó en la expedición napoleónica, extrajo de Estrabón y de Diodoro Sículo la información de que el apotema de la Gran Pirámide tenía un estadio de longitud, es decir, 185,5 metros. Los autores clásicos afirmaban que un estadio era la sexcentésima parte de un grado geográfico. Según esto, el apotema de la pirámide multiplicado por 600 nos daría la longitud de un grado en Egipto. Jomard tuvo en cuenta también la afirmación de Agatárquides de que la largura de cada lado de la base era idéntica a la longitud de un minuto (cada una de las sesenta partes iguales en que se divide un grado de círculo) del meridiano terrestre. Con estos datos se comprueba no sólo el asombroso conocimiento geodésico del planeta que tenían los egipcios, sino la premeditada adecuación de las medidas de la pirámide a las del planeta.
Podría decirse que la pirámide contiene las proporciones de un semiglobo, en el que la base del monumento representa el ecuador y la altura la distancia del Polo Norte al centro del globo. Y, si los antiguos no mentían al señalar que su altura era la sexcentésima parte de un grado de longitud y su base un octavo de minuto, la Gran Pirámide podría ser la representación de una mitad de nuestro planeta.
En relación con las medidas geodésicas de este monumento, numerosos investigadores de todos los tiempos han intentado desentrañar y reproducir la hipotética idea original del arquitecto de la Gran Pirámide y de la unidad de medida empleada.
UN INSÓLITO DESCUBRIMIENTO
Pero hagamos el proceso contrario. Supongamos que queremos construir el monumento más grande de la Tierra, que disponemos de toda la tecnología precisa para tal fin y que queremos incorporar las medidas del planeta a esa pirámide. Partimos de la premisa constatada de que la Tierra no es una esfera perfecta. La figura geométrica que mejor define la superficie de nuestro planeta es un elipsoide de revolución, es decir, un cuerpo engendrado por una elipse, cuyos ejes son los radios polar y ecuatorial, y que gira sobre el radio polar. Actualmente, la geodesia física hace un estudio de la Tierra considerándola un geoide, definiendo su superficie como la de los océanos en calma y los continentes sin tener en cuenta su relieve, es decir, como si toda la tierra estuviese al mismo nivel del mar. Si superponemos las figuras elipsoide y geoide de la Tierra (como si superpusiésemos, por ejemplo, un melón y una sandía), ambas coincidirán en determinadas líneas, que consideraremos "zonas de cota cero".
Queremos, pues, construir una pirámide que cumpla dos condiciones. La primera es que esté situada en el meridiano terrestre donde interseccionen el elipsoide y el geoide antes mencionados (ver figura). Para ello, nos basaremos en un mapa que representa estas dos superficies y sus discrepancias, publicado en el libro Geodesia Física de Weikko A. Heiskanen, donde figuran los antes mencionados puntos de intersección o líneas de cota cero. En él podemos ver que los únicos lugares del planeta donde se cumple esta primera condición son una franja de terreno que recorre el Nilo y otra que, subiendo por la cuenca del Amazonas, llega a la península del Yucatán y a México, siendo exclusivamente la zona de Egipto donde la línea que tiene cota cero en todos sus puntos coincide con el meridiano del lugar.
La segunda condición es que el lugar preciso del emplazamiento de dicha pirámide esté ubicado en aquel paralelo cuyos puntos estén situados en su totalidad a la misma distancia del Polo Norte y del centro de la Tierra. Con ello, obtenemos un solo punto en el planeta que cumpla estas dos premisas: la meseta de Giza, situada en el paralelo 29° 58' 51" norte y longitud 31 ° 9' este de Greenwich.
Asombrosamente, cada punto de la Tierra tiene un radio diferente, debido al achatamiento de los polos. El radio polar –según el anuario del Observatorio Astronómico, que publica las medidas dadas por el Servicio Internacional de la Rotación Terrestre (IERS)– es de 6.356,751 km, siendo el radio ecuatorial de 6.378,136 km. El radio terrestre en la meseta de Giza es de 6.372,829 km.
Hasta hoy se ha especulado mucho en relación con la unidad de medida empleada en la Gran Pirámide. El problema principal reside en la diferencia entre nuestro metro actual, la diezmillonésima parte del cuadrante del meridiano que pasa por Dunkerke y Barcelona, y el metro real egipcio, estimado por el notable egiptólogo Petrie en 1,0479 y por Newton en 1,0478. Por ello han surgido algunas teorías extravagantes que han tratado de hacer coincidir nuestro metro actual con el utilizado en el antiguo Egipto como, por ejemplo, prolongar el radio polar "convenientemente" 300 kilómetros, para elevar nuestro vulgar 1,00 a la categoría de 1,048, definiendo la atmósfera con ese exacto espesor, como si ésta fuese uniforme. Por tanto, los estudiosos más oficialistas han tomado a broma siempre tales consideraciones, afirmando que el metro egipcio no podría corresponderse con dato geodésico o astronómico alguno.
EL METRO SAGRADO EGIPCIO
Y todo lo contrario. Como primicia mundial vamos a demostrar que el metro real egipcio se corresponde con medidas geodésicas de nuestro planeta, de una forma absolutamente constatable. Partimos de la esfera ideal cuyo radio es el radio de la Tierra medido en Giza. Pues bien, la longitud de arco comprendida entre la Gran Pirámide y el polo norte de dicha esfera corresponde a la cifra de 6.673,611 km. Todo este planteamiento nos lleva a dar una simple fórmula que dictamina milimétricamente y con datos geodésicos absolutamente fiables el metro utilizado en la Gran Pirámide:
1 metro egipcio = Radio en Giza x W/60.QOO
Es decir: 6.372,829 x 3,14162/60.000 = 1,048.
Para los amantes de la geometría, se cumple también que la diezmillonésima parte del cuadrante del meridiano de una esfera con radio de 6.673,611 km., sería, precisamente, 1,048 metros, el patrón de medida utilizado en la Gran Pirámide.
Estamos seguros de que estos datos, que publicamos por primera vez, aunque difícilmente comprensibles para los neófitos en geometría y en astronomía, revolucionarán la historia de la piramidología, al relacionar el metro sagrado egipcio, empleado en todas las medidas interiores y exteriores del monumento, con datos geodésicos intrínsecos a la ubicación de la Gran Pirámide en nuestro planeta. Este monumento señala un punto exacto de la superficie terrestre, el mismo punto desde donde se sospecha que alguien situado a unos 10.000 metros de altura pudo tomar una imagen, por métodos desconocidos, del globo terrestre. Aquellas remotas observaciones se plasmaron en antiguos mapas como el de Piri Reis, distorsionado con asombrosa exactitud debido a la falta de concavidad de la fotografía original. Un punto geodésico que señala que los constructores del monumento y, posiblemente, los instructores de los pueblos de la antigüedad, conocían las medidas de nuestro planeta, porque eran poseedores de una tecnología ajena y avanzadísima, sin la cual no podrían haber llegado de ninguna forma a conseguir estos datos.
:: MysteryPlanet ::
|
|
|
|
Reply |
Message 5 of 35 on the subject |
|
Squaring the Circle - The Great Pyramid
|
The square represents the physical. The circle represents the spiritual. All sacred geometers have attempted the impossible: to square the circle (create a square who's perimeter is equal to the circumference of a circle.)
Here is the first of two valiant attempts:
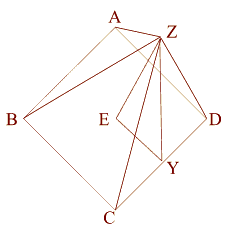
This squaring of the circle works with a right triangle that represents the apothem (ZY) - (a line drawn from the base of the center of one of the sides to top of the pyramid), down to the center of the base (ZE), and out to the point where the apothem touches the Earth (EY).
|

The Great Pyramid of Egypt
(Sphinx in foreground)
|
|
|
Now let's look at this in 2D,
from directly above.
For the purpose of this exercise,
the side (AB) of the base equals 2.
|
|
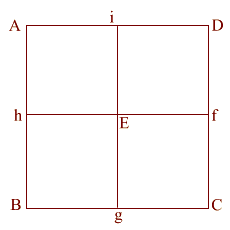
|
(ABCD) is the base of the Great Pyramid.
This is lettered similarly to the wire frame version (above).
For the purpose of this exercise,
the side (AB) of the base equals 2.
|
|

|
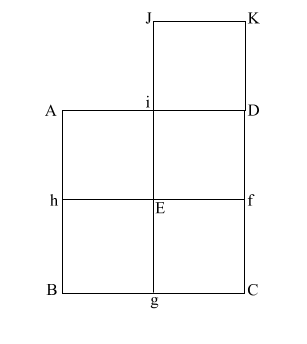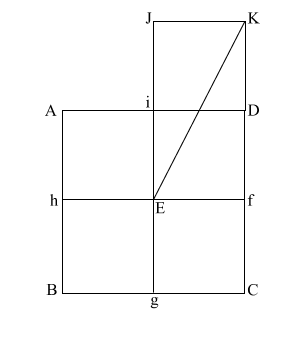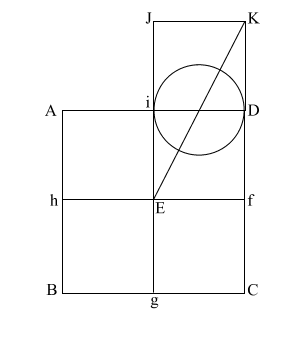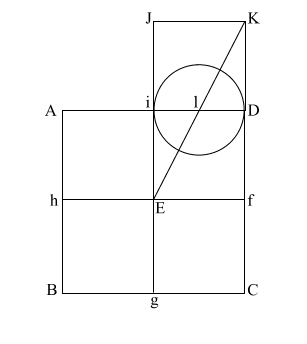
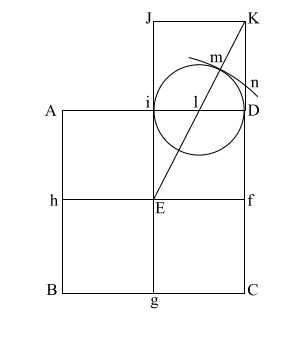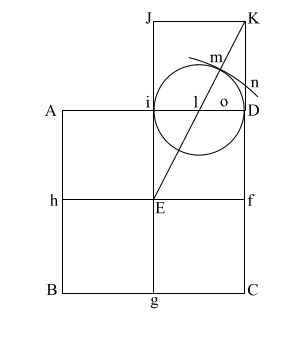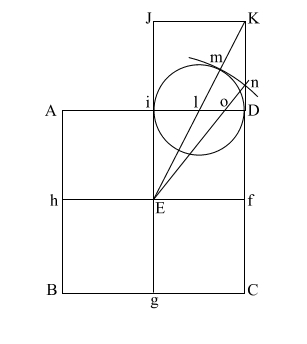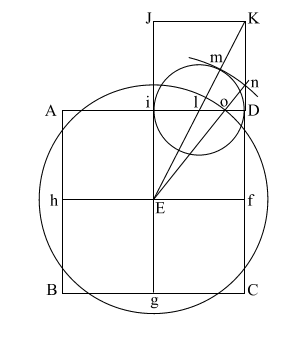
Construct square (i JKD),
thus creating double square (JKE f).
|
|
|
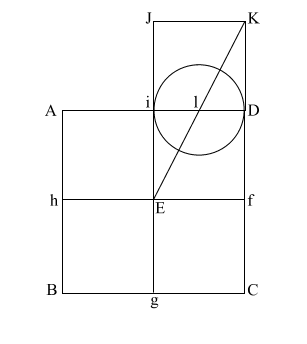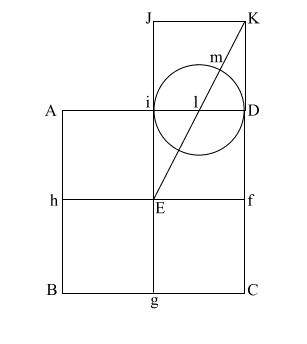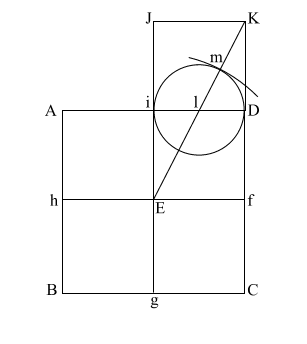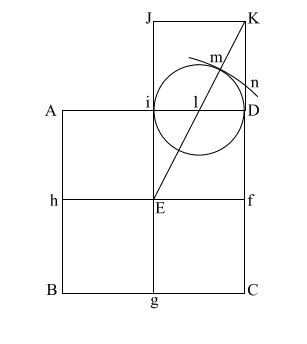
Create diagonal (EK)
which intersects (i D) at (l).
iD = 1,
therefore the diameter
of the circle is also 1.
(EK) = ( 5) = .618 + 1 + .618 5) = .618 + 1 + .618
|
|
|
Put the point of your compass at (E) and extend it along the diagonal (EK) to point (m) where the circle intersects (EK), and draw the arc downward to intersect (KD f C) at (n).
If (EK) = ( 5), and (l m/l D) and l i = .5, the diameter of this circle is 1. 5), and (l m/l D) and l i = .5, the diameter of this circle is 1.
This makes (E m) = .618 + 1, or 1.618.
(E m) is the apothem.
|
|
|
Draw (E n) which intersects (A i l D ) at (o).
Put compass point at (f) and extend it to (n). Again put your point at (E) and draw the circle which happens to have the radius (E o).
(f n) is the height of the Great Pyramid.
This circle comes remarkably close to having the same circumference as the perimeter of the base (ABCD).
|
|
Let's go back to the original right triangle (EYZ)
(EY) = .5
(YZ) = phi
(EZ) = ( phi) phi)
EY = .5, The apothem is phi/1.618. This makes the 51 degree + degree angle.
Using a² + b² = c², this makes the height the square root of phi.
|
Squaring the Circle - The Earth & the Moon
|
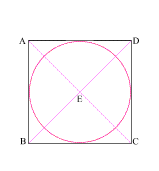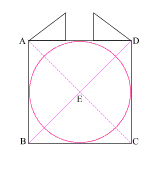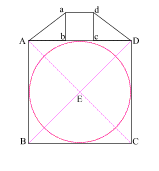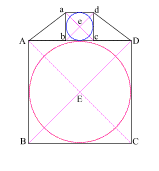
Create a square (ABCD) with (AB) = 11
Create diagonals (AC) and (BD) crossing at center point (E)
Construct a circle which is tangent to square (ABCD) at f
|

|
|
Construct two 3 . 4 . 5 right triangles, with the 4 . 5 angles at (A) and (D).
Connect the 5 . 3 angles creating square (abcd) with side (ab) = 3
{4 + 3 + 4 = 11, or side (AD) of square (ABCD)}
Create diagonals (ac) and (bd) centering at (e)
Create a circle that is tangent to square (abcd) at four places.
|
|
|
Draw line (Ee) which intersects side (AD) at (F)
(EF) = the radius of the larger circle and (eF) = the radius of the smaller circle
The larger circle thus created is to the smaller circle as the moon is to the Earth!
With your compass point at (E), create a circle with radius (Ee)
This creates a circle whose circumference is equal to the perimeter of square (ABCD)!
|

|
The Math:
|
1
(AB) = 11
(EF) = 1/2 of (AB) = 5.5
(ab) = 3
(eF) = 1.5
Therefore 5.5 + 1.5 = 7
The circumference of a circle is equal to two times the radius (the diameter) times pi (3.1416).
C= 14 x 3.1416
C= 43.9824
|
2
In Square (ABCD), (AB) = 11
The perimeter of a square is four times one side. 11 x 4 = 44
According to the Cambridge Encyclopedia, the equator radius of the Earth is 3963 miles. The equator radius of the Moon is 1080.
The claim is that the smaller circle (in square abcd) is to the larger circle (in square ABCD) as the Moon is to the Earth.
|
|
3
(EF) = 5.5
(F e) = 1.5
5.5 : 1.5 :: 3963 : 1080
5.5 / 1.5 = 3.66666
3963 / 1080 = 3.6694 - (if it had been 3960, it would have been exact!)
|
Sacred Geometry
Geomancers are interested in sacred geometry because this is the study of the way that spirit integrates into matter - by echoing and amplifying the geometry of nature and planetary movements, we help to align the resonance of body/mind/spirit with the harmonic frequencies of the above and the below.
Geomancers are interested in sacred geometry because it has been found that certain spaces, with particular ratios, enable the participant to resonate or vibrate at the appropriate rate that maximizes the possibility of connection to the One.
A violin isn't built out of a cigar box! It is built with the proper wood with the proper shape and ratios, so that it resonates correctly for the notes/frequencies it is expected to produce. These same principles are applied to sacred spaces to maximize the possibility that whatever is being done there on spiritual levels will succeed.
Definitions
Two Dimensions
I've been a student of sacred geometry for over twenty-five years. While there has been recent interest in three-dimensional sacred geometry based on the Platonic Solids and in sacred sites themselves, most sacred geometrical documents I've read talk in only two dimensions - height and width.
Obviously there is a fourth dimension and others beyond it that are much more complex and sophisticated. But why does the record left to us from geomancers of the past come primarily in two dimensions?
Two is closer to the One than three is. It's less complex. I think one of the biggest mistakes Western geomancers have made was to take something that is very simple and make it much more complex. The Chartres Labyrinth strikes me as being an example of this. This stuff is simple. If you really gnow (that is, know both rationally and intuitively) a handful of irrational ratios - pi ( ), phi (Ø) and the square roots of two, three and five, you've basically got it all. ), phi (Ø) and the square roots of two, three and five, you've basically got it all.
Three-dimensional sacred geometry just builds on this basic handful.
Numbers
One aspect of Sacred Geometry is that it works with irrational numbers. To go to the spiritual, one must go beyond the rational, and it appears that some of these ratios and numbers can lead us there. By being inside a sacred space that has been constructed using one of a handful of these sacred geometrical ratios, the resonance that has been set up can enhance the possibility of your making the spiritual connection you want to make.
So, what are these irrational numbers? Let's begin with the rational.
Rational Numbers
A rational number is a number which can be expressed as the ratio of two integers (whole numbers), such as 1/3 or 37/22. All numbers which, when represented in decimal notation, either stop after a finite number of digits or fall into a repeating pattern, are rational numbers.
Irrational Numbers
An irrational number is one that cannot be represented as a ratio of any two whole-number integers, and consequently it does not fall into a repeating pattern of any sort when written in decimal notation.
All of the Sacred Geometry ratios we will be working with, the square roots of two (1.414), three (1.732) and five (2.238), phi (1.618) and pi (3.1416), are all irrational numbers.
Transcendental Numbers
There are certain kinds of irrational numbers that are called transcendental numbers. Just like irrational numbers, they are defined by what they are not (they aren't rational numbers), yet transcendental numbers are so identified because they are not another sort of number, known as an algebraic number.
Any number which is a solution to a polynomial equation is an algebraic number. A polynomial equation is a sum of one or more terms involving the same variable raised to various powers, for example:
7 (x5) + 5 (x3) + x = 137
Any X for which any such equation is true is an algebraic number. Because the square root of two is a solution to the polynomial equation,
x2 = 2
it is an algebraic number.
A transcendental number requires an infinite number of terms to be defined exactly. That's one way of thinking of God/dess. There are special equations to derive transcendental numbers where the terms get smaller and smaller as you go along, so you can keep adding them together to reach any level of accuracy you need, but the true number cannot be reached exactly. That is the beauty of transcendental numbers!
Pi ( = 3.1416...) is such a transcendental number. It is the only one we will be using here with Sacred Geometry. One infinite equation which relates to the value of pi ( = 3.1416...) is such a transcendental number. It is the only one we will be using here with Sacred Geometry. One infinite equation which relates to the value of pi ( ) is this: ) is this:
Pi / 4 = 1 - (1/3) + (1/5) - (1/7) + (1/9) - (1/11) + (1/13) - (1/15) + ...and so on into infinity.
http://www.bibliotecapleyades.net/geometria_sagrada/esp_geometria_sagrada_3.htm
|
|
|
 First
First
 Previous
2 a 5 de 35
Next
Previous
2 a 5 de 35
Next Last
Last
|

