The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
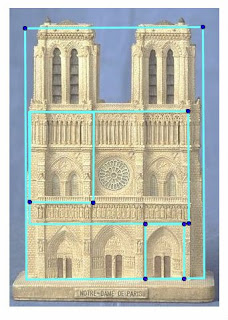
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/