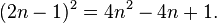|
|
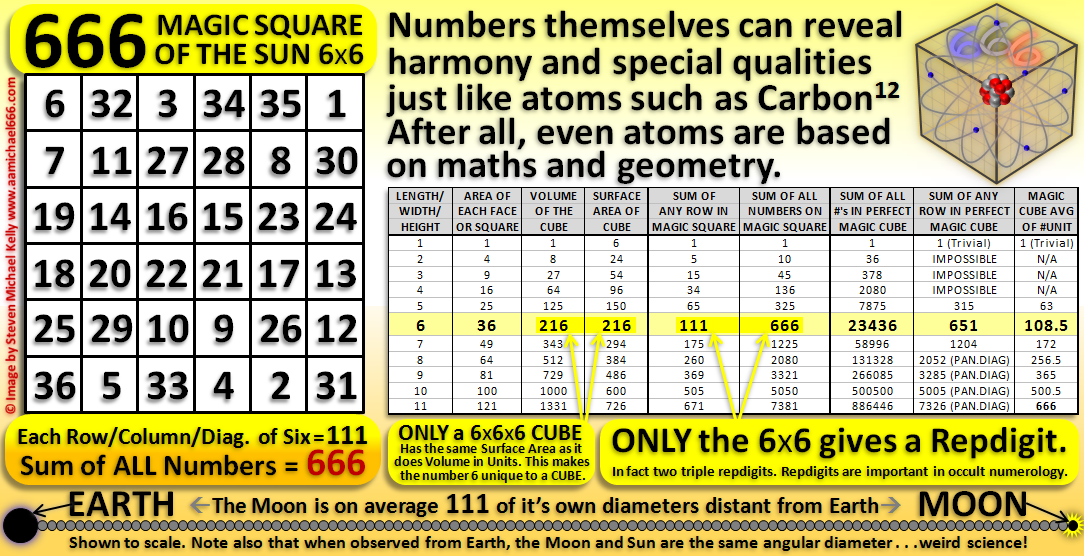
Propiedades numéricas del 6, 60, 216 y 666
Martes, 11 agosto 2009 por qbit
Índice.
Introducción.
6.
60: Sistema sexagesimal.
216.
666.
Introducción.
He recopilado las propiedades numéricas más importantes o llamativas de los números 6, 60, 216 y 666, que son números relacionados entre sí.
Este artículo de Matemáticas sirve de introducción al siguiente, un artículo sobre numerología (esoterismo), aplicada en sociopolítica, religión y misticismo de los números 6, 216, 666 y 6 millones.
Antes de continuar, es necesario ser consciente de la ley fuerte de los números pequeños, según la cual, los números pequeños, al ser pocos, aparecen por todas partes e intervienen en multitud de casualidades numéricas. Esto no debe llevar a engaño y hacer creer que dichas casualidades son más especiales o que señalan algo mágico. Todos los números pequeños “disfrutan” de muchas curiosidades numéricas.
6.
Euclides llamó al número 6 “perfecto” por ser igual a la suma de sus divisores (6 = 1+2+3). Desde entonces a los números que tienen esta propiedad se les llama perfectos: 28, 496, 8128, …
El 6 es el menor número perfecto.
Es el segundo número compuesto más pequeño.
Es el tercer número triangular: T(3) = 6· T(8) = 36 (6 · 6) también es triangular.
Es un número octahedral.
Es un número congruente.
Es el único número resultado de la suma y el producto de tres enteros positivos.
Es un número perfecto unitario, un número divisor armónico y un número altamente compuesto.
60: Sistema sexagesimal.
El sistema sexagesimal es un sistema de numeración de base 60 (6 x 10), cuyo origen procede de los sumerios, pasando luego a los babilonios. El sistema sexagesimal se usa para medir tiempos (horas, minutos y segundos) y ángulos (grados, minutos y segundos). En este sistema, 60 unidades de un orden forman una unidad de orden superior. El número 60 tiene la ventaja de tener muchos divisores (2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60), con lo que se facilita el cálculo con fracciones. 60 es el número más pequeño que es divisible por 1, 2, 3, 4, 5 y 6:
Unidades de tiempo:
- 1 minuto = 60 segundos (6 · 10)
- 1 hora = 60 minutos (6 · 10)
- 1 día = 24 horas (6 · 4)
- 1 semana = 7 días (6 días laborables + 1 de descanso)
- 1 mes = 30 días (6 · 5)
- 1 año = 12 meses (6 · 2) = 360 + 5 días (6 · 6 · 10 + 5)
Unidades de ángulos:
- Minuto de arco = 60 segundos de arco (6 · 10)
- Grado = 60 minutos de arco (6 · 10)
- Círculo = 360 grados (6 · 6 · 10)
Se ve claramente la relación entre grados de circunferencia y tiempo. Supongo que la medición del tiempo con relojes circulares y manecillas que miden segundos y minutos procede de la trigonometría (y la astronomía) sexagesimal, o al revés.
El calendario chino está formado por 5 ciclos de 12 años cada uno (60 años en total).
El sextante es un antiguo instrumento de navegación que mide ángulos entre dos objetos lejanos. El nombre sextante proviene de la escala del instrumento, que abarca un ángulo de 60 grados, un sexto de un círculo completo.
El sistema de numeración babilónico era base 60. Pero a diferencia del sistema decimal que tiene 10 símbolos distintos para representar los números, los babilonios sólo empleaban 2 símbolos que combinados producían los 60 símbolos de su sistema de numeración, el cual tenía vestigios de un sistema de numeración decimal.
En geometría euclidiana: Todos los ángulos internos de un triángulo equilátero tienen 60º. La suma de los grados de los ángulos internos de cualquier triángulo es 180º (6 · 3 · 10).
Relación con los números primos: Divisores de 60 son los tres primeros números primos: 2, 3 y 5. También son números primos el anterior y el siguiente al 60: 59 y 61.
Relación con el número 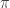 : Ptolomeo usaba para : Ptolomeo usaba para 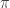 una gran aproximación: una gran aproximación:
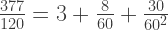
216.
216 es el volumen del cubo formado por un lado de longitud 6: 216 = 63.
También es el más pequeño cubo que es la suma de 3 cubos consecutivos: 216 = 63 = 33 + 43 + 53.
Es la suma de dos primos gemelos: 216 = 107 + 109.
Es un número intocable.
Es un número de Harshad en base 10.
216 = φ(666), en donde la función φ de Euler es la cantidad de números enteros menores que 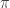 y coprimos con y coprimos con 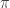 . .
666.
Es un número abundante.
Forma parte de los índices de la secuencia de Padovan de números primos.
Propiedades como repdigit (número con todos los dígitos iguales):
- Es un repdigit.
- Es el repdigit triangular más grande.
- Propiedad de los repdigits: La media armónica de los dígitos decimales de 666 es un número entero: 6 =
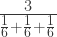
Relación con números primos:
- Es la suma de dos números primos capicúas consecutivos: 666 = 313 + 353.
- La cantidad de números primos hasta 666 es 121, y 121 es la cantidad de números primos hasta 36.
- Es la suma de los cuadrados de los primeros 7 números primos: 666 = 2² + 3² + 5² + 7² + 11² + 13² + 17²
- Es un número de Smith: 666 = 2·3·3·37 y 6+6+6 = 2+3+3+3+7
- φ(666) = 6·6·6 = 216.
- 902659997773 es el menor número primo cuyo inverso tiene un periodo de 666 decimales de longitud.
Relaciones numéricas:
- 6 = 1 − 22 + 32
- 66 = 1 − 24 + 34
- 666 = 16 – 26 + 36
- 666 =64 – 63 – 63 – 63 + 6 + 6 + 6
- 666 =6 + 6 + 6 + 6·(6·6 + 6·6 + 6·6)
- Es la suma de sus dígitos más los cubos de sus dígitos: 666 = 6 + 6 + 6 + 63 + 63 + 63 (hay en total 6 números con esta propiedad).
- 666 es un divisor de 123456789 + 987654321 (observar que dichos números son la concatenación de todos los dígitos del 1 al 9, y del 9 al 1), como también lo son los siguientes:
- 666 = 1 + 2 + 3 + 4 + 567 + 89 = 123 + 456 + 78 + 9
- 666 = 9 +87 + 6 + 543 + 21
- Suma capicúa de cubos: 666 = 13 + 23 + 33 + 43 + 53 + 63 + 53 + 43 + 33 + 23 + 13.
Fracciones:
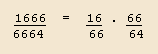
Relaciones numéricas pitagóricas y triangulares:
- Es el 36º número triangular: T(6·6) = 666 = 1 + 2 + 3 + 4 … + 34 + 35 + 36 (y 36 = 6·6).
- Es el 8º número doblemente triangular (aplicación: hay 666 maneras de pintar los vértices de un cuadrado con 8 colores).
- Es el repdigit triangular más grande.
- Es el número triangular más pequeño de la forma a2 + b2, siendo a+b también triangular. Ejemplo:
- T(6·6) = 666 = T(5)2 + T(6)2 = 152 + 212, siendo 15 y 21 a su vez números triangulares consecutivos.
- El triplete (216, 630, 666) es un triplete pitagórico (la suma de los cuadrados de los primeros = al cuadrado del tercero): (6·6·6)² + (666 – 6·6)² = 666²
- Se conocen dos triángulos pitagóricos cuya área es un número repdigit, y ese número repdigit está relacionado con el 6 y el 666: (3, 4, 5) con área 6, y (693, 1924, 2045) con área 666666.
Relación con (6² + n²):
666 = (6 + 6 + 6) · (6² + 1²)
666 = 6! · (6² + 1²) / (6² + 2²)
Relación con constantes superimportantes:
- Es la suma de los primeros 144 dígitos de
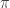 , en donde 144 = (6+6)(6+6). , en donde 144 = (6+6)(6+6).
- Φ = -2 sen (666 º) = -2 cos (6·6·6 º) = -(sen (666 º) + cos (6·6·6 º)) = -(sen (666 º) + cos (66·6 º)) = -(sen (666 º) + cos (666 º)) = -(sen (666 º) + cos (666666 º))
En donde Φ es la razón áurea y 6·6·6 = 216.
En números romanos, DCLXVI = 666, que es precisamente la concatenación de los primeros 6 dígitos romanos de mayor a menor.
|
|
|
|
|
https://es.wikipedia.org/wiki/Sistema_sexagesimal
Sistema sexagesimal
El sistema sexagesimal es un sistema de numeración posicional que emplea como base aritmética el número 60. Tuvo su origen en la antigua mesopotamia, en la civilización sumeria. También fue empleado por los árabes durante el califato omeya. El sistema sexagesimal se usa para medir tiempos (horas, minutos y segundos) y ángulos (grados, minutos y segundos).
Introducción
El número 60 tiene la ventaja de tener muchos divisores (1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60), con lo que se facilita el cálculo con fracciones. Nótese que 60 es el número más pequeño que es divisible por 1, 2, 3, 4, 5 y 6.
El uso del número sesenta como base para la medición de ángulos, coordenadas y medidas de tiempo se vincula a la vieja astronomía y a la trigonometría. Era común medir el ángulo de elevación de un astro y la trigonometría utiliza triángulos rectángulos. En la Antigüedad, lo que ahora llamamos números enteros positivos —excluido el cero— eran los únicos números "bona fide". Los números racionales actuales eran considerados razones entre números enteros, pues la filosofía imperante recurría a la proporción y una fracción, en definitiva, era una comparación proporcional entre dos segmentos de valores enteros. Todo esto vinculado a lo que llamamos mínimo común múltiplo. Todos los triángulos rectángulos de lados enteros tienen la propiedad de que el producto de sus tres lados es siempre un múltiplo de sesenta. Si uno de los catetos es primo, el otro es al menos múltiplo de doce y resulta múltiplo de sesenta si también la hipotenusa es prima. Si no hay cateto primo, un cateto es divisible por tres y el otro por cuatro; cualquiera de los tres lados es múltiplo de cinco. Esta penúltima afirmación tiene por excepción al triángulo sagrado egipcio, que tiene un cateto primo y la hipotenusa prima, pero el cateto compuesto es múltiplo de cuatro: (3, 4, 5), aunque el producto es sesenta. Otros ejemplos de triángulos con cateto e hipotenusa primos son: (11, 60, 61) y (71, 2520, 2521).
Quedan vestigios del sistema sexagesimal en la medición del tiempo. Hay 24 horas en un día, 60 minutos en una hora y 60 segundos en un minuto. Las unidades menores que un segundo se miden con el sistema decimal.
Para expresar los números en el sistema sexagesimal, se sigue un convenio que consiste en emplear los números del sistema decimal (de 0 a 59), separados de dos en dos por comas. Para indicar la coma decimal, se emplearía un punto y coma sexagesimal. Por ejemplo, el número 1;07,30 corresponde a 1 + 07/60 + 30/60² = 1,125 en decimal. durante el Califato Omeya, el sistema sexagesimal fue empleado por los árabes tanto para contar el tiempo como para la geometría y trigonometría que había evolucionado de los ancestros babilónicos, pasando por el viejo Egipto y muchas otras culturas. Fueron precisamente los árabes quienes asentaron el uso del sistema sexagesimal en la cultura moderna, ya que durante casi 500 años ostentaron todo el potencial científico sin discusión. Al igual que en su momento los babilonios trazaron las primeras líneas para que los árabes utilizaran su sistema años después, estos cimentaron el uso del sistema sexagesimal tal y como lo conocemos hoy día. Y por muy curiosos que resulte todavía sigue funcionando a la perfección.
Suma y resta del sistema sexagesimal en las matemáticas
El sistema sexagesimal es un sistema de numeración en el que cada unidad se divide en 60 unidades de orden inferior, es decir, es su sistema de numeración en base 60. Se aplica en la actualidad a la medida del tiempo y a la de la amplitud de los ángulos.
1 h 60 min 60 s
1º 60' 60"
Operaciones en el sistema sexagesimal
Suma
1.er paso Se colocan las horas debajo de las horas (o los grados debajo de los grados), los minutos debajo de los minutos y los segundos debajo de los segundos; y se suman.
2o paso Si los segundos suman más de 60, se divide dicho número entre 60; el resto serán los segundos y el cociente se añadirá a los minutos.
3.er paso Se hace lo mismo para los minutos.
Resta
1.er paso Se colocan las horas debajo de las horas (o los grados debajo de los grados), los minutos debajo de los minutos y los segundos debajo de los segundos.
2o paso Se restan los segundos. Caso de que no sea posible, convertimos un minuto del minuendo en 60 segundos y se lo sumamos a los segundos del minuendo. A continuación restamos los segundos.
3.er paso Hacemos lo mismo con los minutos.
Origen
Al igual que en el caso del sistema decimal, el origen se remonta a una manera de enumerar usando los dedos de las manos. En la Antigüedad los habitantes del llamado Creciente Fértil contaban señalando con el dedo pulgar de la mano derecha, si se era diestro, cada una de las 3 falanges de los restantes dedos de la misma mano, comenzando por el meñique. Con este método se puede contar hasta 12. Y para seguir con cifras mayores, cada vez que realizaban esta operación se levanta un dedo de la mano libre —la izquierda— hasta completar 60 unidades (12 x 5 = 60), por lo que este número fue considerado una «cifra redonda», convirtiéndose en una referencia habitual en transacciones y medidas. Similar suerte corrió el número contado en la mano derecha, el 12, y algunos múltiplos como 24, 180 (12 x 15, o bien 60 x 3) y 360 (12 x 30, o bien 60 x 6). Por esto, el sistema sexagesimal se emparenta en su raíces históricas con el sistema duodecimal.
Esta forma de contar con los dedos (hasta 12 y, luego, hasta 60) sigue siendo usada en la actualidad por algunos habitantes del Medio Oriente.1
El matemático Sergei Fomin reseñaba otras dos antiguas explicaciones sobre el origen del sistema sexagesimal, aunque él las consideraba poco creíbles y pobremente argumentadas. La primera hipótesis era que el sistema sexagesimal surgió del compromiso político entre dos tribus que se confederaron, combinando sus respectivos sistemas numéricos (senario y decimal). La segunda, presentada el sistema como un derivado de la observación astronómica y no un resultado del uso cotidiano. De tal forma que, como los mesopotámicos establecieron su año en 360 días, habrían concluido el uso de un divisor de ese número (el 60) como cifra base de toda su numeración.2
El uso astronómico en el origen
En Babilonia se dividió la circunferencia en 360 arcos iguales. Cada una de esas partes recibió el nombre de grado y a cada una de ellas se le asignó un dios. En el zodíaco vuelve a aparecer el doce, pues esa cantidad de signos o «casas» tiene el sistema, abarcando un arco de 30 grados y un conjunto de la misma cantidad de dioses. El sistema religioso era muy estricto y dogmático y exigía que los ángulos fueran construidos mediante regla no graduada de un solo borde y longitud indefinida, más un compás de abertura fija, mientras se trazaba una circunferencia, pero que se cerraba al levantarlo, con lo que no era posible usarlo para transportar segmentos o medidas (Ver: Regla y compás). Este sistema de construcción geométrica era considerado de origen y uso divino; según estas creencias el universo había sido creado con ese método de construcción geométrica.
Lo que constituye un misterio es saber cómo se desarrolló plenamente ese sistema religioso geométrico, ya que el Teorema General de Ciclotomía de Gauss, de 1801, demuestra imposible la construcción para muchos ángulos de un número entero de grados: cualquiera que no sea múltiplo de 3º.
Es un problema abierto determinar si los sacerdotes se conformaron con aproximaciones o con métodos no sagrados, como hacer marcas en la regla. Esto hubiera destruido toda una filosofía y si hubiese ocurrido tendrían que haberlo escondido cuidadosamente de los hombres cultos no pertenecientes al clero.
Cada 315 años el Sol y la Luna vuelven a situarse en el mismo lugar en el firmamento, con un error de 7 u 8 minutos de arco. Esto constituye un poco más del doble de la separación mínima que puede detectar el ojo humano sin instrumentos de aumento. El pequeño error debería tener un significado religioso ignorado por nuestra civilización, puesto que el grado era ocupado por un dios y se dividía en 60 minutos. Pero tanto el Sol como la Luna caían en el mismo dominio «divino». Cuatro períodos abarcan 1260 años, que equivalen a 3 + ½ veces 360 años. Llevando el conjunto a su mínima expresión entera tenemos el período astronómico de 2520 años, que forma parte de un triángulo rectángulo con un cateto y la hipotenusa primos: (71, 2520, 2521). Estos números, 1260 y 2520, son múltiplos de 12, 40 y 60 y pueden ocupar cualquier cateto y la hipotenusa de triángulos rectángulos semejantes al triángulo sagrado egipcio (3, 4, 5) y, en general, de cualquier triángulo rectángulo de lados enteros, en especial de aquellos con un cateto primo.
Ejemplos
-
- 1,414212... = 30547/21600 = 1;24,51,10 (sexagesimal = 1 + 24/60 + 51/60² + 10/60³),
- una constante que ya fue utilizada por los matemáticos babilonios del Periodo Babilónico Antiguo (1900 a. C. – 1650 a. C.), y que se recoge en la tablilla de barro YBC 7289. Un valor más exacto de
 es 1;24,51,10,07,46,06,04,44,... es 1;24,51,10,07,46,06,04,44,...
-
- 365,24579... = 06,05;14,44,51 (365 + 14/60 + 44/60² + 51/60³).
-
- 3,141666... = 377/120 = 3;08,30 (3 + 8/60 + 30/60²).
Fracciones
El número 60 tiene como divisores primos los tres primeros números primos, es decir, 2, 3 y 5. Cualquier fracción cuyo denominador sea de la forma 2a · 3b · 5c tendrá un desarrollo sexagesimal exacto, con a, b y c números enteros iguales o mayores que 0.
Sin embargo, en los casos en que el desarrollo no es exacto, el periodo será generalmente largo. Como tanto el número anterior como el posterior a 60 son primos (59 y 61, respectivamente), para que el periodo sólo sea de una o dos cifras el denominador tiene que ser 59, 61, el producto de los dos (3599) o cualquiera de los anteriores por un número de la forma 2a · 3b · 5c. En cualquier otro caso, el periodo será más largo.
- 1/2 = 0;30
- 1/3 = 0;20
- 1/4 = 0;15
- 1/5 = 0;12
- 1/6 = 0;10
- 1/7 = 0;08,34,17
- 1/8 = 0;07,30
- 1/9 = 0;06,40
- 1/10 = 0;06
- 1/11 = 0;05,27,16,21,49
- 1/12 = 0;05
- 1/13 = 0;04,36,55,23
- 1/14 = 0;04,17,08,34
- 1/15 = 0;04
- 1/16 = 0;03,45
- 1/17 = 0;03,31,45,52,56,28,14,07
- 1/18 = 0;03,20
- 1/19 = 0;03,09,28,25,15,47,22,06,18,56,50,31,34,44,12,37,53,41
- 1/20 = 0;03
- 1/24 = 0;02,30
- 1/25 = 0;02,24
- 1/27 = 0;02,13,20
- 1/30 = 0;02
- 1/32 = 0;01,52,30
- 1/36 = 0;01,40
- 1/40 = 0;01,30
- 1/45 = 0;01,20
- 1/48 = 0;01,15
- 1/50 = 0;01,12
- 1/54 = 0;01,06,40
- 1/59 = 0;01
- 1/1,00 = 0;01 (1/60 en decimal).
Tablas de multiplicar
Las tablas de multiplicar en base-sesenta son relativamente difíciles de memorizar, ya que se trata de memorizar 59×60/2 = 1770 productos distintos. A modo de comparación, en el sistema decimal hay que memorizar 9×10/2 = 45 productos. ejemplo:
8*5=40 1.8 2.8 3.8 4.8 5.8=40
Búsqueda de números primos
Los números primos pueden terminar en las siguientes cifras: 01, 07, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 49, 53 o 59.
En otras palabras, si tenemos un número natural cuya última cifra, en base-sesenta, es un número primo (que no sea 02, 03 o 05), el 01 o el 49, entonces ese número puede ser primo — y se podría comprobar empleando algún método de primalidad. Si no termina en alguna de esas cifras, entonces tiene que ser compuesto.
Referencias
Bibliografía
- Dantzig, Tobías (1971). El Número. Lenguaje de la Ciencia. Buenos Aires: Editorial Hobbs Sudamericana. (Traducido de la cuarta edición en inglés). El libro hace una historia de la evolución del concepto de número para el lector culto no matemático. Tuvo un comentario elogioso de Albert Einstein y fue referencia para la reforma educativa en Argentina. Trata acerca de los sistemas de numeración y del completo desarrollo del concepto de número, no explicando deliberadamente los conceptos que no son asimilables por un lector no matemático como, por ejemplo, los ideales. Particularmente en él se encontrará una demostración incompleta del teorema que dice que el producto de los lados de un triángulo rectángulo es siempre múltiplo de sesenta, ubicada en la página 295 de la referencia antecitada; esto debido a una omisión en cuanto al carácter primo de un cateto. Se editó por lo menos cuatro veces en inglés en los Estados Unidos de América y dos en español en Argentina. La referencia corresponde a la segunda edición en Argentina y la primera fue realizada por otra editorial en 1947.
Notas
Historia Universal. Volumen I, Prehistoria y primeras civilizaciones. Editorial Sol90, 2004. pag 69.
|
|
|
|
|
| Reply |
Message 19 of 19 on the subject |
|
|
|
|
|
|
|
|
DETRAS DE LAS "TEORIAS DE CONSPIRACION" HAY MENSAJES CON FUERTE REFERENCIA AL SANTO GRIAL, QUE LOS PSEUDOINTELECTUALES, CON MUCHA SED DE PODER (GENERALMENTE OLIGARCAS YA SEA POR ISQUIERDA O POR DERECHA) NO LOGRAN DESCIFRAR POR SU FUERTE IDOLATRIA AL DIOS DINERO- TEMPLO DE MARIA LA MAGDALENA EN VENECIA / VENUS / (SAN MARCOS)
TOM HANKS
FRANK/BANK/KEY
ANK/LIBERTAD
¿CUAL ES EL SECRETO DETRAS DEL PAPA ARGENTINO FRANCISCO /FRANK?
Mitterrand built a pyramid
EL BUHO/CERRADURA ES LA MISMA VIRGEN MARIA LA MAGDALENA NUESTRA MADRE
EL ORO REFINADO ES EL GRIAL MISMO
714. Mateo 23:17: ¡Insensatos y ciegos! porque ¿cuál es mayor, el ORO, o el templo que santifica al ORO?
|
|
|
|
|
The New Jerusalem Decagon
Professor D.G. Leahy discovered a "hidden circle" (the green circle) within the New Jerusalem pattern --
It is effectively the value of the diameter (= 11) of the decagon formed by the double helix structure of the DNA molecule, which decagon is visible in the top-down view of the molecule. See --
DNA, APOCALYPSE, & THE END OF THE MYSTERY
The New Jerusalem plan is based on Revelation 21, and indicates the order of the heavens made apparent on earth.
Numbers that relate to the diagram include 7920 (Earth diameter), and 5040 (radius of the Earth plus the radius of the moon 3960 + 1080). Remember, the base ten harmonics of the first two numbers (792 and 504) were revealed in the Crooked Soley DNA crop circle formation (792 + 504 = 1296).
The sub-lunar distance around the New Jerusalem is figured (using Pyramid Pi 22/7) --
(2 x 22/7) x 5040 = 31680
This is represented by the circle just inside the green circle above, which passes through the center of the twelve "Moon" circles.
Another interesting calculation is the distance across the New Jerusalem, figured as --
Moon diameter + Earth diameter + Moon diameter
2160 + 7920 + 2160 = 12240
The number 12240 is part of the 153 Fish in the Net story --
153 x 80 = 12240
|
|
|
|
|
The New Jerusalem Diagram – The Blueprint for Ancient Monuments?
May 15, 2012

“The city was laid out as a square, its length equal to its breadth. The angel measured the city with a rod and it was 12,000 stadia in length and breadth and height. He measured its wall, and this was 144 cubits high, according to the human measure he used.” — Revelation 21:16-17
Modern science confirms what our ancestors already new: the architecture of the universe (nature) is based on some key numeric proportions we can see on all levels of scale: from the atoms and DNA, through patterns and blueprints of life, all the way to solar system and galaxies…
NOTE: The New Jerusalem Diagram is also known as The Cosmological Circle
The New Jerusalem Diagram – Introduction
“The New Jerusalem Diagram” is the name given by the scholar of ancient lore, John Michell [The original explanations in John Michell's books, especially "The Dimensions of Paradise", Thames and Hudson, 1986] to a geometrical construction that allows the “squaring of the circle” and the division of the circle to 28 equal sectors (a zodiac wheel) and the ceremonial positioning of the twelve tribes (or constellations) in a pattern of four camps at the four sides of the square.
John Michell has reconstructed the geometric pattern of the ‘heavenly city’ which is the template of the New Jerusalem of Revelation 21.

He discovered that this diagram served as the design (blueprint) for many sacred sites, including the Stonehenge, The Great Pyramid, St. Mary’s Chapel at Glastonbury and the City of Magnesia in Plato’s The Laws.

The Great Pyramid, Earth and Moon fit the New Jerusalem Diagram
It turns out that also the Nazca glyph called “Mandala” aka “Sun-Star-Cross” perfectly matches the New Jerusalem Diagram.



Superimposed image of NJ Diagram and Mandala glyph near Nazca, Peru
It is no surprise that the NJ diagram matches blueprint for the The Dome of the Rock, a shrine located on the Temple Mount in the Old City of Jerusalem.

The wheel of 28 divisions is common to various esoteric systems and serves as representation for the schematic month: 4 weeks = 28 days. The solar calendar of the Dead Sea scrolls sect was of 364 days, which is a multiple of 28 ( 28×13 = 364). In many Sufi diagrams, including in the ceiling of the dome at the El-Aqsa Mosque* (not the Dome of the Rock) at the Temple Mount, there appears the motif of the wheel made of 28 divisions.

Al-Aqsa. The resplendent ceiling of the Al-Aqsa Mosque on the Temple Mount in Jerusalem. The mosque, one of Islam’s most holy sites, sits near the Dome of the Rock and above the Marwani Mosque, aka Solomon’s Stables.
Image Source/Credit.
The NJ diagram is also hinted and enfolded (according to Micheell), in the description of the holy city, The New Jerusalem, whose descent from heaven concludes the Christian Bible.

Below we present 3-D version of the New Jerusalem Diagram.

Is it possible the 3D NJ diagram was used as a blueprint for the Crown Jewels?… Perhaps this is a case of a “secret hidden in plain site”?


The collective term Crown Jewels denotes the regalia and vestments worn by the sovereign of the United Kingdom during the coronation ceremony and at other state functions. The term refers to the following objects: the crowns, sceptres (with either the cross or the dove), orbs, swords, rings, spurs, colobium sindonis, dalmatic, armill, and the royal robe or pall, as well as several other objects connected with the ceremony itself. The Crown Jewels have a religious and sacral connotation. Their hidden symbolism seems to be related to the sacred geometry of the New Jerusalem Diagram.
The Construction of the New Jerusalem Diagram
The construction of this diagram starts with the attempt to “square the circle” by drawing a circle and a square that have the same circumference.
- So in building this sacred diagram, one starts with a circle with a diameter of 22 units, and blocks it with a square of 22 x 22 units (like the number of the Hebrew letters, with which supposedly “heaven and earth were made”).
- Then one draws from the same centre an additional circle whose diameter is 28 units – “the perfect number” that is already the number of the letters in the first verse of genesis and marks the circle of the seasons. The circle with diameter 28 has circumference of Pi x 28, which is as noted 22/7 x 28 = 88 – just the circumference of the square with edges of 22 and circumference thus 2 x 22 = 88.
The circle and the square have the same circumference, and they intersect in 8 points, where the square juts out of the circle in 4 vertices.

- The building of the complete pattern continues with the drawing of 12 circles with diameter of 6 units – the number of letters in the first word of Genesis – Bereshit – as the first “perfect number”. The centers of these twelve circles are situated on the outer big circle, whose diameter is 28, and they touch (are tangent to) the inner circle, whose diameter is 22. Four of these circles are situated according to the points were the square is tangent to the inner circle, and the other 8 circles are placed according to the 8 points of intersection between the square and the outer circle.

There are two amazing consequences of this construction:
- This construction squares the circle
- It divides the circle into 28 equal segments
- It reflects ratio 22:7 which is good approximation of the “Pi”
- It reflects golden ratio 1.618
- It reflects the ratio of 22:6, which issues theoretical-geometrical considerations is also the exact real ratio between the diameter of the earth and the diameter of the moon!

There are many more features of the NJ diagram which will be presented in our upcoming articles (e.g. amazing connection with Teotihuacan).
|
|
|
|
|
|
 Dome of the Rock The floor plan of the Dome of the Rock and some construction lines; possible source of inspiration for Templar constructions and the cross pathee
_________________
Everything is Connected and there are no
coincidences
|
|
Centered octagonal number
From Wikipedia, the free encyclopedia
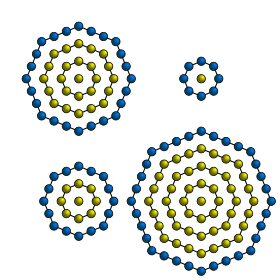
A centered octagonal number is a centered figurate number that represents an octagon with a dot in the center and all other dots surrounding the center dot in successive octagonal layers.[1] The centered octagonal numbers are the same as the odd square numbers.[2] Thus, the nth centered octagonal number is given by the formula
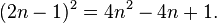
The first few centered octagonal numbers are[2]
- 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089.
Calculating Ramanujan's tau function on a centered octagonal number yields an odd number, whereas for any other number the function yields an even number.[2]
See also[edit]
References[edit]
https://en.wikipedia.org/wiki/Centered_octagonal_number
The New Jerusalem Diagram – Introduction
“The New Jerusalem Diagram” is the name given by the scholar of ancient lore, John Michell [The original explanations in John Michell's books, especially "The Dimensions of Paradise", Thames and Hudson, 1986] to a geometrical construction that allows the “squaring of the circle” and the division of the circle to 28 equal sectors (a zodiac wheel) and the ceremonial positioning of the twelve tribes (or constellations) in a pattern of four camps at the four sides of the square.
John Michell has reconstructed the geometric pattern of the ‘heavenly city’ which is the template of the New Jerusalem of Revelation 21.

He discovered that this diagram served as the design (blueprint) for many sacred sites, including the Stonehenge, The Great Pyramid, St. Mary’s Chapel at Glastonbury and the City of Magnesia in Plato’s The Laws.

The Great Pyramid, Earth and Moon fit the New Jerusalem Diagram
It turns out that also the Nazca glyph called “Mandala” aka “Sun-Star-Cross” perfectly matches the New Jerusalem Diagram.



Superimposed image of NJ Diagram and Mandala glyph near Nazca, Peru
It is no surprise that the NJ diagram matches blueprint for the The Dome of the Rock, a shrine located on the Temple Mount in the Old City of Jerusalem.

The wheel of 28 divisions is common to various esoteric systems and serves as representation for the schematic month: 4 weeks = 28 days. The solar calendar of the Dead Sea scrolls sect was of 364 days, which is a multiple of 28 ( 28×13 = 364). In many Sufi diagrams, including in the ceiling of the dome at the El-Aqsa Mosque* (not the Dome of the Rock) at the Temple Mount, there appears the motif of the wheel made of 28 divisions.

Al-Aqsa. The resplendent ceiling of the Al-Aqsa Mosque on the Temple Mount in Jerusalem. The mosque, one of Islam’s most holy sites, sits near the Dome of the Rock and above the Marwani Mosque, aka Solomon’s Stables.
Image Source/Credit.
The NJ diagram is also hinted and enfolded (according to Micheell), in the description of the holy city, The New Jerusalem, whose descent from heaven concludes the Christian Bible.

Below we present 3-D version of the New Jerusalem Diagram.

Is it possible the 3D NJ diagram was used as a blueprint for the Crown Jewels?… Perhaps this is a case of a “secret hidden in plain site”?


The collective term Crown Jewels denotes the regalia and vestments worn by the sovereign of the United Kingdom during the coronation ceremony and at other state functions. The term refers to the following objects: the crowns, sceptres (with either the cross or the dove), orbs, swords, rings, spurs, colobium sindonis, dalmatic, armill, and the royal robe or pall, as well as several other objects connected with the ceremony itself. The Crown Jewels have a religious and sacral connotation. Their hidden symbolism seems to be related to the sacred geometry of the New Jerusalem Diagram.
The Construction of the New Jerusalem Diagram
The construction of this diagram starts with the attempt to “square the circle” by drawing a circle and a square that have the same circumference.
- So in building this sacred diagram, one starts with a circle with a diameter of 22 units, and blocks it with a square of 22 x 22 units (like the number of the Hebrew letters, with which supposedly “heaven and earth were made”).
- Then one draws from the same centre an additional circle whose diameter is 28 units – “the perfect number” that is already the number of the letters in the first verse of genesis and marks the circle of the seasons. The circle with diameter 28 has circumference of Pi x 28, which is as noted 22/7 x 28 = 88 – just the circumference of the square with edges of 22 and circumference thus 2 x 22 = 88.
The circle and the square have the same circumference, and they intersect in 8 points, where the square juts out of the circle in 4 vertices.

- The building of the complete pattern continues with the drawing of 12 circles with diameter of 6 units – the number of letters in the first word of Genesis – Bereshit – as the first “perfect number”. The centers of these twelve circles are situated on the outer big circle, whose diameter is 28, and they touch (are tangent to) the inner circle, whose diameter is 22. Four of these circles are situated according to the points were the square is tangent to the inner circle, and the other 8 circles are placed according to the 8 points of intersection between the square and the outer circle.

There are two amazing consequences of this construction:
- This construction squares the circle
- It divides the circle into 28 equal segments
- It reflects ratio 22:7 which is good approximation of the “Pi”
- It reflects golden ratio 1.618
- It reflects the ratio of 22:6, which issues theoretical-geometrical considerations is also the exact real ratio between the diameter of the earth and the diameter of the moon!

There are many more features of the NJ diagram which will be presented in our upcoming articles (e.g. amazing connection with Teotihuacan).
|
|
|
|
|
|
 Primer Primer
 Anterior
172 a 186 de 771
Siguiente Anterior
172 a 186 de 771
Siguiente Último
Último
|













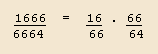

 es 1;24,51,10,07,46,06,04,44,...
es 1;24,51,10,07,46,06,04,44,...