|
Réponse |
Message 1 de 28 de ce thème |
|
La Gran Pirámide de Keops: pi por la raíz de fi es casi cuatro
Cuaderno de bitácora: publicamos hoy otro de los artículos que en su día aparecieron en doDK. Este artículo fue escrito hace más de seis años. En él explico un descubrimiento que hice por mí mismo, una extraordinaria coincidencia que se da en las proporciones de la Pirámide de Keops y que implica, necesariamente, una no menos extraordinaria coincidencia entre dos de los números más conocidos de las matemáticas.
[Vista de las tres grandes pirámides de la planicie de Giza o Gizeh. No hay que confundirse: la pirámide de Keops, la Gran Pirámide, es la que está más a la derecha, más atrás en la foto. La del medio es la de Kefrén, la segunda en altura, aunque en la foto parece más alta por estar más cerca, y la tercera la de más a la izquierda, la de Micerinos. La pirámide de Kefrén es muy fácil de reconocer porque conserva en su parte superior algo del revestimiento original. Es muy frecuente que se hable de la Gran Pirámide de Keops y sin embargo en las imágenes, erróneamente, aparezca la pirámide de Kefrén, la más fotogénica de las tres]
La gran pirámide de la planicie de Gizeh, la conocida como pirámide de Keops, siempre ha sido una fuente de misterios, y la mayoría están aún por resolver. Sus medidas han sido estudiadas exhaustivamente por todos los inquietos de los enigmas antiguos, y con los datos obtenidos podemos afirmar que los Egipcios no construyeron la pirámide dándole unas medidas al azar, sino que sus proporciones mantienen unas relaciones matemáticas muy interesantes entre sí.
La gran pirámide medía originalmente 147 metros de altura, y el lado de la base tenía una longitud de 230 metros, aproximadamente. Hoy en día la pirámide es un poco más baja, porque a lo largo de los siglos y sobre todo en la Edad Media ha sido utilizada de cantera artificial. Las piedras de las que estaba compuesta se han ido partiendo y tallando en ladrillos más pequeños para servir de material a algunos monumentos levantados en el pasado en la ciudad de El Cairo. Así la pirámide, que en su origen tenía una superficie pulida y blanca y estaba rematada por una punta de oro, se puede contemplar hoy como cuando contemplamos una casa vieja y a punto de derrumbarse, en la que se ven los ladrillos porque la capa de yeso que recubría la pared se ha caído con el tiempo.
Hace ya muchos años descubrí en cierto libro que las proporciones de la pirámide guardaban una importante relación: cuatro veces el lado de la base dividido por dos veces la altura daba el número pi. Esto es lo mismo que decir que si tomamos la altura de la pirámide como radio de una circunferencia, la longitud de la circunferencia coincide con el perímetro de la base.
Si tomamos como datos los que hemos mencionado anteriormente, h = 147 metros, y b = 230 metros. Haciendo la cuenta, 4·b = 920, 2·h = 294, y dividiendo ambas cantidades obtenemos 3'1292517..., es decir, aproximadamente 3'13. Teniendo en cuenta que tanto la altura de la pirámide como el lado de la base se han tomado de forma aproximada, es normal esperar que el resultado no coincida exactamente con el número pi.
Si tomamos en cuenta unas medidas más exactas, como las que aparecen en el libro De las mentiras de la Egiptología a las Verdades de la Gran Pirámide, de Luis García Gallo, la altura sería de 146'7 metros y el lado de la base de 230'4 metros (aproximadamente). Volviendo a hacer los cálculos con estas dos nuevas aproximaciones tenemos que 4·b/(2·h) = 3'14110429... y aquí ya nos vamos aproximando más al número pi. De hecho el error es del orden de 0’016%.
El error es mínimo y totalmente admisible ya que en arquitectura, lo mismo que en todas las demás ciencias aplicadas, las medidas tienen un límite de precisión. De hecho, los cuatro lados de la base de la pirámide no miden exactamente lo mismo, sino que se diferencian en algunos centímetros. De la misma forma las desaparecidas Torres Gemelas no eran exactamente igual de altas, sino que una era un poco más alta (creo que como medio metro) que la otra. A todo esto hay que añadir los estragos del tiempo sobre los monumentos. Las medidas obtenidas son aproximadas sobre una estimación de lo que la pirámide medía cuando la construyeron, hace casi cinco mil años, porque ahora las medidas son muy distintas...
La relación entre b y h se puede expresar así:
Es decir, la proporción entre b y h es como la de pi a 2.
Consultando la página de matemáticas Epsilones descubrí algo nuevo para mí. Según el historiador Heródoto, los Egipcios construyeron la gran pirámide de tal forma que el área de cada una de las caras triangulares laterales coincidiera con el área de un cuadrado de lado igual a la altura. Teniendo en cuenta lo que acabamos de decir, nos encontramos con las siguientes fórmulas:
Vamos a buscar la proporción entre a, b y h:
Dividimos por b cuadrado y consideramos a/b como una incógnita:
Hemos suprimido la solución negativa porque tanto a como b son números positivos (estamos tratando con longitudes de la pirámide).
De repente nos ha aparecido el número áureo, fi), un número no tan conocido como pi, pero muy importante en la historia de las matemáticas:
De aquí tenemos la relación entre a y b, y por ende entre b y h:
Con esto tenemos que la proporción entre a y b es como la de fi a 2, y la proporción entre b y h es como la de 2 a la raíz cuadrada de fi.
Resumiendo, si los Egipcios construyeron la pirámide con las proporciones mencionadas por el historiador Heródoto, entonces la pirámide de Gizeh es proporcional a una que tenga como altura de una de las caras laterales a fi y como lado de la base a 2:
Entonces surge la cuestión de si ambas propiedades de la pirámide son consistentes, la de pi y la de fi. ¿Cuál de las dos propiedades es la que guió a los constructores de la pirámide? ¿O los constructores quisieron incluir adrede ambas características en su diseño?
Supongamos que somos los constructores, y el faraón nos ordena que levantemos una pirámide en la que el perímetro de la base dividido entre dos veces la altura dé el número pi. Como ya conocemos el número pi, sólo tenemos que preguntarle al faraón la altura que quiere que tenga, y tras unos cálculos sencillos, obtenemos todas las dimensiones, el lado de la base, la longitud de las aristas, etc. Pero el faraón nos dice poco después que además quiere que el área de una de las caras laterales sea igual al área de un cuadrado de lado igual a la altura.
¿Pueden ser posibles ambas cosas? Nosotros ya hemos hecho los cálculos de todas las dimensiones y ya casi nos hemos puesto manos a la obra... Sólo podemos esperar que la suerte nos acompañe y que efectivamente y casi por casualidad se cumpla la segunda condición que nos pide nuestro rey.
¡Y la suerte está de nuestro lado!
Para que se cumpla la condición de pi, b y h tienen que estar en proporción de pi a 2. Para que se cumpla la condición de fi, b y h tienen que estar en proporción de 2 a raíz de fi. Si queremos que se cumplan las dos condiciones, ambas proporciones han de ser iguales:
Bueno, esto no es cierto exactamente, pero sí aproximadamente:
De hecho el error que se comete es menor al 0'1%. Eso quiere decir que con un error del 0'1% podemos construir una pirámide que cumpla las dos condiciones, guardando dentro de sus proporciones al número pi y al número fi. Y la pirámide de Keops es un ejemplo de ello.
Maravilloso, ¿verdad? Y todo porque pi por la raíz de fi es casi cuatro.
Notas: no fui el primero en descubrir esta coincidencia entre los números pi y fi. En el libro de Martin Gardner, Los Mágicos Números del Doctor Matrix, en el capítulo de las pirámides, se habla sobre la curiosa relación entre el número pi y el número fi que posibilita que la Gran Pirámide de Keops cumpla dos propiedades matemáticas diferentes. Sin embargo, honestamente, no leí ese contenido del libro hasta este mismo año pasado, 2009, seis años después de escribir este artículo.
Por otro lado, han quedado plasmados mis esfuerzos para expresar la notación matemática en un artículo de la web. No soy muy experto todavía en esto, y la solución que encontré en su momento fue la de usar el editor matemático del Microsoft Word para escribir la expresión que quería, y luego guardar dicha expresión como archivo de imagen, para incluirlo en el artículo. Los gráficos de las pirámides los realicé con el sencillo programa Paint que viene incluido en Windows.
|
|
|
|
Réponse |
Message 2 de 28 de ce thème |
|

Pi es un número irracional con infinitos decimales, y puede ser calculado hasta un mínimo de dos decimales, si tenemos el suficiente conocimiento teórico de geometría –cosa que los antiguos egipcios nunca tuvieron– Es imposible conseguir con el experimento de la rueda un resultado más preciso de Pi que “3.14 +/- 0.05″, así que si encontramos un valor mucho más preciso en las dimensiones de un edificio nos encontramos con una irrefutable prueba de un conocimiento matemático muy avanzado.
Los antiguos egipcios simplemente usaban 3 como multiplicador, y esta medida les era suficiente para la mayoría de las aplicaciones cotidianas. Mucho más adelante, centenares de años después de la construcción de las grandes pirámides, fue cuando comenzaron a usar la medida 3 + 1/7.
Pi-rámide
La Gran Pirámide de Keops tiene una base de 230,38m de longitud y una altura de 146,6m. Si tomamos dos veces la longitud de la base, y la dividimos por su altura, obtenemos el valor de “3.14297…”. Es una gran aproximación al valor de Pi, mejor que el valor que los antiguos egipcios pudieron haber estimado con su medida de 3, por lo que… ¿estamos ante el signo evidente de un diseño por parte de una entidad superior? La respuesta de los científicos es un claro ‘No’. ¿Por qué no, tienen una mejor explicación que darnos?

Algunos dicen que este valor de Pi en la pirámide es simple coincidencia –bastante coincidencia, igualar el valor de Pi al cuarto decimal–. Además, hay otras muchas pirámides dimensionadas con el valor de Pi, incluso con mayor precisión. ¿Más coincidencias?
No parece, así que otros científicos han encontrado una teoría que explicaría la misteriosa presencia de Pi en las pirámides. Sugieren que la presencia de Pi en Keops se debe a los métodos de medida usados en tiempos antiguos. Los egipcios median distancias en “codos reales”, que equivalían a 0,523 metros. La base de la pirámide de Keops es exactamente de 440 codos reales de largo, y su altura de 280 codos. ¿Cómo hacían los egipcios para medir distancias tan grandes?

Los científicos sugieren que el uso de cuerdas sería impracticable en estos casos (las cuerdas de estas dimensiones se romperían o cambiarían su longitud debido a la enorme presión ejercida para mantenerlas en tensión). Entonces, lo más probable es que los egipcios utilizaran ruedas del diámetro de un codo real para medir las distancias, haciéndolas rodar y contando las revoluciones (cada giro completo de la rueda). Y, como hemos visto en el ejemplo de la rueda de antes, es aquí donde Pi dejaría su impronta en las medidas finales. Cuando los egipcios querían medir la altura de la pirámide, simplemente tenían que apilar unas ruedas encima de las otras y contarlas.
Parece una teoría muy plausible y razonable, y puede explicar la relación entre Pi y las medidas de pirámides como las de Keops y Medum, así que la teoría ha tenido gran repercusión y ha pasado a ser la explicación más aceptada sobre el tema. El problema es que no es válida para explicar el resto de pirámides. Para la pirámide de Kefren, este cálculo da un resultado de “3″, mientras que para la de Micerinos el valor de Pi resultante es de “3,26″. No son valores de Pi aceptables, y finalmente, de las 90 pirámides que hay en Egipto la teoría sólo explica satisfactoriamente las medidas de dos o tres de ellas. Así que ¿por qué aceptar una teoría que sólo explica unas poquísimas pirámides?, ¿no es probable que los antiguos egipcios construyeran todas sus pirámides con técnicas similares?
Incluso para los casos como Keops en que la teoría parece cierta, tomando sus 440 codos reales de longitud y empleando una medida como la propuesta habría que hacerlos girar exactamente 140,0564 veces (440/Pi), y habría que apilarlos 130,825 veces para obtener la altura de la pirámide deseada. Sin un conocimiento verdadero del valor de Pi real, que recordemos no se ha podido demostrar que los egipcios tuvieran, no sería posible averiguar estos valores fraccionarios. Además, el sistema numérico egipcio era muy diferente al nuestro y, entre otras diferencias, no manejaba decimales, y la única fracción que manejaba era “uno partido por algo”, marcado por un signo oval encima del número. Un matemático egipcio ni entendía ni podía representar el número “2,537″, por ejemplo.
El ángulo de las pirámides
Hay una explicación todavía más sencilla a todo este misterio, y tiene que ver en cómo los ingenieros egipcios medían los ángulos. Era diferente de nuestro sistema actual de medir la inclinación entre dos planos perpendiculares, desconocido para algunas culturas antiguas. En el caso egipcio se basaba en medir la distancia horizontal de la pendiente necesaria para alcanzar la parte superior de un codo real. Esta distancia se medía en palmos o dedos, y eran necesarios un máximo de 28 de ellos para cubrirla.
Los ingenieros egipcios usaban únicamente la medida de los dedos para construir sus edificios. Debido a ello, disponían de un máximo de 28 ángulos posibles para sus edificaciones, que variaban entre el ratio 1 dedo : 1 codo real (casi 90 grados) hasta 28 dedos : 1 codo real (unos 45 grados). De hecho, todas las pirámides encontradas en Egipto trabajan con alguno de estos ángulos.
El más común de todos –y el más atractivo para el ojo humano– es el ratio 1:22 (22 dedos por codo real). Es el utilizado en la Gran Pirámide. Los ratios inferiores a 1:20 eran imposibles de utilizar en la construcción de edificios monumentales (los podemos ver en los edificios a medio acabar de Meidum, y en la pirámide de Dahschur. Por el contrario, los ratios mayores de 1:24 también son raros de encontrar en las obras egipcias, ya que visualmente eran muy poco atractivos. Algunos ejempos de ratios usados en las pirámides: Kefren 1:21, Micerinos 1:23, Djedefre 1:23, pirámide escalonada de Djoser 1:25.

Pirámide escalonada de Sakkara

Pirámide acodada de Seneferu

Pirámide de Djoser

Pirámide de Keops. Clicka para verla en toda su inmensidad
¿Y qué sucede con Pi entonces? Resulta que el ratio 1:22 se aproxima mucho a su valor: 3,14285714 en la pirámide de Chufus, 3,142974 en el caso de Keops. La diferencia con respecto a Pi es de ¡menos de 0,00015! Pero probablemente no es más que una coincidencia, y es el ratio de 1:22 codos reales:dedos el que la provoca.
El factor que nos indica que la relación de Pi con las pirámides probablemente se trata de una coincidencia es que de las 90 pirámides egipcias censadas, hay bastante variación en sus aproximaciones a Pi de unas a otras. Si realmente este concepto matemático hubiera sido conocido y utilizado hace más de 5.000 años, todas las pirámides tendrían una similitud a Pi mucho más aproximada. De las 14 pirámides que nos han llegado en buen estado de conservación, 6 de ellas están construídas en ángulo de ratio 1:22, el ratio Pi.
Parece más seguro creer que estamos ante 90 pirámides con diferentes aproximaciones al valor de Pi, cuya casualidad es debida al sistema de medidas usado en el Antiguo Egipto, que creer que nos encontramos ante una pirámide construida por los dioses, de valor Pi casi perfecto, y otras 89 pirámides de los mismos periodos históricos cuyos ángulos no se pueden explicar de la misma manera. ¿Qué opináis vosotros? |
|
|
|
Réponse |
Message 3 de 28 de ce thème |
|
El Sagrado Número PI y las PI-rámides de Egipto

Mucho antes de que se pusieran de moda las teorías sobre la construcción de las pirámides de Egipto que hablan de alienígenas o habitantes de la Atlántida, se pensaba que éstas eran obra de Dios. Los primeros cristianos y musulmanes creían que las pirámides eran refugios construidos para sobrevivir al Diluvio Universal. Ya en el siglo XIX, algunos descubrimentos sugirieron que la construcción de las pirámides estuvo influenciada por alguna entidad superior. Estas teorías llevaron a la creación de nuevas pseudociencias: “matemáticas de las pirámides“, “numerología” y de tipo astrológico que relacionan la constelación de Orion con las pirámides de Gizah, entre otras. Desde entonces, muchos han creído que las misteriosas conexiones numéricas encontradas en estas obras magnas forman parte de un gran plan. La más famosa de estas conexiones numéricas es la omnipresencia del misterioso número Pi en el monumento más grande jamás construído por el hombre en piedra, la pirámide de Keops.
¿Qué es Pi, y cómo puede encontrarse en la Gran Pirámide?
Pi, en si mismo, no es ninguna invención mágica o misteriosa. Se trata simplemente del valor por el que tenemos que multiplicar el diámetro de un círculo para obtener su circunferencia. El valor aproximado de Pi (3,141592…) se puede obtener a partir de experimentos simples. Cogemos por ejemplo una rueda de un metro de diámetro, la hacemos girar hasta que toda su superficie haya tocado el suelo, y no es ningún secreto que el recorrido que habrá hecho la rueda estará alrededor de los 3,14 metros. O igual de sencillo, podemos rodear la superficie de la rueda con una cuerda, y medir su longitud. Nos dará 3,14 metros igualmente.
|
|
|
|
Réponse |
Message 4 de 28 de ce thème |
|
Apocalipsis Capítulo 21
Vi un cielo nuevo y una tierra nueva; porque el primer cielo y la primera tierra pasaron, y el mar ya no existía más. 2 Y yo Juan vi la santa ciudad, la nueva Jerusalén, descender del cielo, de Dios, dispuesta como una esposa ataviada para su marido. 3 Y oí una gran voz del cielo que decía: He aquí el tabernáculo de Dios con los hombres, y él morará con ellos; y ellos serán su pueblo, y Dios mismo estará con ellos como su Dios. 4 Enjugará Dios toda lágrima de los ojos de ellos; y ya no habrá muerte, ni habrá más llanto, ni clamor, ni dolor; porque las primeras cosas pasaron.
5 Y el que estaba sentado en el trono dijo: He aquí, yo hago nuevas todas las cosas. Y me dijo: Escribe; porque estas palabras son fieles y verdaderas. 6 Y me dijo: Hecho está. Yo soy el Alfa y la Omega, el principio y el fin. Al que tuviere sed, yo le daré gratuitamente de la fuente del agua de la vida. (Aqui se esta haciendo REFERANCIA AL SALMO 119 QUE COMIENZAN Y FINALIZAN CON LAS LETRAS HEBREAS. AQUI ESTA EXPRESADO CON LAS GRIEGAS POR SU OBVIA ESCRITURA EN DICHO IDIOMA. EL AGUA DE LA VIDA TIENE FUERTE NEXO CON EL UNGIMIENTO DE BETANIA Y OSHANAH RABBAH)
¿PORQUE MARIA MAGDALENA UNGE LOS PIES DE JESUS EN
7 El que venciere heredará todas las cosas, y yo seré su Dios, y él será mi hijo.
8 Pero los cobardes e incrédulos, los abominables y homicidas, los fornicarios y hechiceros, los idólatras y todos los mentirosos tendrán su parte en el lago que arde con fuego y azufre, que es la muerte segunda.
Vino entonces a mí uno de los siete ángeles que tenían las siete copas llenas de las siete plagas postreras, y habló conmigo, diciendo: Ven acá, yo te mostraré la desposada, la esposa del Cordero. 10 Y me llevó en el Espíritu a un monte grande y alto, y me mostró la gran ciudad santa de Jerusalén, que descendía del cielo, de Dios, 11 teniendo la gloria de Dios. Y su fulgor era semejante al de una piedra preciosísima, como piedra de jaspe, diáfana como el cristal. (La gloria tiene un fuerte nexo sabatico segun EXODO 24)
12 Tenía un muro grande y alto con doce puertas; y en las puertas, doce ángeles, y nombres inscritos, que son los de las doce tribus de los hijos de Israel; 13 al oriente tres puertas; al norte tres puertas; al sur tres puertas; al occidente tres puertas. 14 Y el muro de la ciudad tenía doce cimientos, y sobre ellos los doce nombres de los doce apóstoles del Cordero.
15 El que hablaba conmigo tenía una caña de medir, de oro, para medir la ciudad, sus puertas y su muro. 16 La ciudad se halla establecida en cuadro, y su longitud es igual a su anchura; y él midió la ciudad con la caña, doce mil estadios; la longitud, la altura y la anchura de ella son iguales. (Efectivamente la GRAN PIRAMIDE ES LA CUBICACION DE UNA ESFERA)
17 Y midió su muro, ciento cuarenta y cuatro codos, de medida de hombre, la cual es de ángel. 18 El material de su muro era de jaspe; pero la ciudad era de oro puro, semejante al vidrio limpio; 19 y los cimientos del muro de la ciudad estaban adornados con toda piedra preciosa. El primer cimiento era jaspe; el segundo, zafiro; el tercero, ágata; el cuarto, esmeralda; 20 el quinto, ónice; el sexto, cornalina; el séptimo, crisólito; el octavo, berilo; el noveno, topacio; el décimo, crisopraso; el undécimo, jacinto; el duodécimo, amatista. 21 Las doce puertas eran doce perlas; cada una de las puertas era una perla. Y la calle de la ciudad era de oro puro, transparente como vidrio.
22 Y no vi en ella templo; porque el Señor Dios Todopoderoso es el templo de ella, y el Cordero. 23 La ciudad no tiene necesidad de sol ni de luna que brillen en ella; porque la gloria de Dios la ilumina, y el Cordero es su lumbrera. 24 Y las naciones que hubieren sido salvas andarán a la luz de ella; y los reyes de la tierra traerán su gloria y honor a ella. 25 Sus puertas nunca serán cerradas de día, pues allí no habrá noche. 26 Y llevarán la gloria y la honra de las naciones a ella. 27 No entrará en ella ninguna cosa inmunda, o que hace abominación y mentira, sino solamente los que están inscritos en el libro de la vida del Cordero.
Vamos con las medidas de la Gran Pirámide. Pongamos que aproximadamente la base mide 230,30 metros, que la altura original era de 146,6 y la apotema de sus caras (la línea que recorre todo el centro de la cara) es de 186,3. Pues bien, si simplificamos estas medidas y consideramos que la base mide 2, la altura mediría 1,272 y la apotema sería 1,618. Es decir, un triángulo que tenga como base 2, como altura 1,272 y como los lados 1,618, tendría las mismas proporciones que la Gran Pirámide en su corte transversal. La altura divide a ese triángulo en dos triángulos rectángulos menores que tendrían como base 1, como altura 1,272 y como hipotenusa 1,618.
O sea, que la Gran Pirámide está edificada teniendo como armazón a un triángulo rectángulo que tiene como base la unidad de medida, como altura la raíz del número Fi (1,618). Por lo que queda demostrado que el número Fi está incorporado a la Gran Pirámide sin distorsionar ninguna medida. Por si acaso hubiera dudas, la secante del ángulo de 51 grados y 51 minutos (ángulo de inclinación de la Gran Pirámide) es 1,618 (Fi) y por ende el coseno de 51 grados y 51 minutos es el inverso de Fi (0,618).
Las medidas de la Gran Pirámide resuelven la cuadratura de la circunferencia. Demostración: La circunferencia que tiene como radio la altura de la pirámide tiene la misma longitud que la base cuadrada de la Gran Pirámide.
Radio = 146,6 x 2Pi = 921
Lado de Base = 230,30 x 4 = 921
Lo cual implica que si dividimos la base de la pirámide por el doble de la altura obtenemos el número Pi.
Las medidas de la Gran Pirámide resuelven la cuadratura del círculo. Demostración: un rectángulo formado por la base de la Gran Pirámide y su altura tiene la misma superficie que un semicírculo que tenga como radio la altura de la pirámide.
Superficie del semicírculo = Pi x radio2 /2 = 33.758
Superficie del rectángulo = 230,3 x 146,6 = 33.761
Las medidas de la Gran Pirámide resuelven la cubicación de la esfera. Demostración: según la geometría, la mitad de un círculo plano es también matemática y rigurosamente igual en área a la superficie esférica de un cuadrante de 90 grados. O sea, que un rectángulo cuya altura y base sean las de la pirámide tiene la misma superficie que un cuadrante esférico cuya altura sea la de la pirámide y su arco la base de la Gran Pirámide.
Superficie del cuadrante esférico = arco x radio = 230,3 x 146,6 = 33.761
Superficie del rectángulo = 230,3 x 146,6 = 33.761.
Otra demostración: la superficie del prisma generado tomando la base y la altura de las caras de la Gran Pirámide (una caja donde se pudiera meter la Gran Pirámide) tiene la misma superficie que la semiesfera generada tomando como radio la altura de la Gran Pirámide.
Base x altura 230,3 x 146,6 x 4 caras = 135.047
Superficie de la semiesfera = 4 x Pi R2 / 2 = 4 x Pi x 146,6 x 146,6 /2 = 135.035.
Ahora nos enfrentamos a un problema con dos posibles soluciones:
1. Los constructores de la Gran Pirámide adquirieron en tiempos de Keops el conocimiento de los números Pi y Fi e inmediatamente después se olvidó en Egipto tal conocimiento, en una absoluta pérdida de memoria sin parangón conocido en la historia de la ciencia.
2. Los egipcios, que desconocían estas proporciones, no pudieron construir ni siquiera el boceto arquitectónico de la Gran Pirámide. Pero esa es otra historia.
|
|
|
|
Réponse |
Message 5 de 28 de ce thème |
|
PHI es la 21a letra del AlfaBeto griego. El valor del número PHI es 1,6180339. Este número es la relación proporcional entre 6.765 y 4.181, primeros números enteros que la producen, es decir que 6.765 es 1'6180339 veces el número 4.181, o 6.765 dividido por 4.181 da PHI.
Estos dos números pertenecen a la llamada "serie de Fibonacci" y forman la 19º división. La serie reproduce mediante números enteros una secuencia de evolución entre crecimiento y proporción que las personas que lo han investigado dicen que se da en muchos elementos de la Naturaleza. Por eso se le da en llamar la Divina Proporción, el Número de Oro o el Número Áureo. En algunos casos nuestra propia intuición/corazón percibe la armonía/belleza subyaciendo a las proporciones de las formas sin necesidad de acudir al intelecto para realizar comprobaciones ni cálculos ni demostraciones a otros intelectos "alejados" de la intuición.
La serie es resultado de una lógica sencilla y consiste en que, comenzando por el número 1 el siguiente número es la suma de los dos anteriores. Así, si tenemos el 1 para obtener el siguiente hemos de sumar 0+1 que es 1. Y el siguiente es 1+1 que es 2, y así sucesivamente:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765...
El 144 es el 12º número de la serie y es el cuadrado de 12, es decir 12 x 12.
Las divisiones son:
1/1 = 1
2/1 = 2
3/2 = 1'5
5/3 = 1'666
8/5 = 1'6 (en 8 órbitas al Sol (8 años) la Tierra se encuentra 5 veces con Venus al mismo lado del Sol).
13/8 = 1'625 (relación entre el periodo orbital de la Tierra y de Venus: 365 días / 225 días. En 13 órbitas de Venus, la Tierra da 8 órbitas).
21/13 = 1'6153846
34/21 = 1'6190476
55/34 = 1'617647
89/55 = 1'6181818. Primera división que produce 3 decimales.
144/89 = 1'6179775
233/144 = 1'6180555. División que da 4 decimales.
377/233 = 1'6180257
610/377 = 1'6180371
987/610 = 1'6180327
1597/987 = 1'6180344
2584/1597 = 1'6180338
4181/2584 = 1'6180340
6765/4181 = 1'6180339
El número Phi, como el Pi, no es entero. Su valor con 3 decimales es 1'618. Si lo sumamos a sí mismo una y otra vez llegaremos a un valor cuasientero, el 88'99, prácticamente 89, tras 55 sumas.
1'618 x 55 = 88'99 ó 89. La curiosidad, al "integrar" phi (nada que ver con "integrales") o estirarlo 55 veces dando 89, es que los números 55 y 89 son números consecutivos de la serie. Y el siguiente cuasientero es 144'002 = Phi x 89, ó Phi escalado 89 veces. El 144 es el 12º número de la serie y es el cuadrado de 12, es decir 12 x 12.
En la siguiente animación puedes construir una espiral como las de las conchas de los nautilus en base a una estructura geométrica basada en cuadrados proporcionales. Puedes pulsar sobre el punto rojo para iniciar la construcción. |
|
|
|
Réponse |
Message 6 de 28 de ce thème |
|
1444,000 in Pyramid
The Great Pyramid of the Lord at Giza had 144,000 casting stones to cover its sides. They now have all been looted and used elsewhere, but it is extremely significant to note, that this is exactly the number of believers the Lord says will be in His Encampment in the End Times (SEE 144,000). This along with the fact, that the sarcophagus within the Kings Chamber of the Great Pyramid had exactly the same inner measurements as the Ark of the Covenant, again confirms that the Great Pyramid corresponds to the Lord’s measure and numbers as written in the Bible. (SEE Giza Sacrophagus and Ark)
But in case, you still don’t believe this, notice that the Giza square base was 792 feet in length when you add the wall that was originally around it. This sacred number was used because it is the Great Number 72 times 11, the magical unseen number. 72 x11 = 792. New Jerusalem, of course just being a magnification of this pyramid, as it measured 12,000 furlongs square. (Revelation 21: 16) Converting into feet, making it 12,000 times 660 = 7,920,000 feet. Consequently Giza is a 1/10,000 miniature of New Jerusalem. Or vice versa, New Jerusalem is a 10,000 magnification of the Great Pyramid. (SEE New Jerusalem is a Phi Pyramid)
But then again, New Jerusalem will also be placed upon the Earth, just as Giza sits upon the Earth. And the Earth itself also uses the 792 factor as its length, even though it’s in miles and is the diameter of its sphere. 7920 miles x 5280’/mile = 41,817,600. This meaning that the temple of the Earth is 5.28 times as large as the temple of New Jerusalem … 41,817,600/7,920,000 = 5.28 (1.1x 1.2 x 4).
But as mentioned with all pyramids there has to be a wall around them so as to keep out those that are unworthy. ‘And he (the Lord’s angel) measured the wall thereof, an hundred and forty cubits according to the measure of a man, that is of the angel.’ Consequently we know the wall’s depth, 144 cubits which again relates directly back to the number 144,000. Coincidence, NO WAY, as the Lord’s consistently uses the same numbers and templates because they are harmonic together.
Still don’t see it or believe it, well 144 cubits is 216 feet because a cubit is the length from our finger tips to our elbow and is 1 and a half feet in length, the measure of a man. And 216 is number involved with the diameter of the MOON. ….2160 miles. The Moon reflected the light of the SUN, just as 144,000 casing stones of the Great Pyramid did. And Biblically, this same reflection is seen as the Lord’s virgin of 144,000 reflects the glory of the Bridegroom.. JESUS. Coincidence NO !!
And furthermore as if you needed more proof, together the Earth and the Moon mated together in UNION, would yield 7290 + 2160 diameters = 10080 miles diameter. This meaning that the Moons diameter would magnify the Earth’s diameter by .272 to a total of 10080/7920 ….. 1.272. And that is the height of a PHI PYRAMID, because it is the square root of PHI (1.618). So like the Great Pyramid and New Jerusalem, even the joining of the Moon and earth, Bride and Bridegroom also create a PHI TEMPLE of Love. (SEE Earth, Moon Phi Graphics). And furthermore, according to Lambert Dolphin, the original temple area covered 5000 cubits by 500 cubits, this giving sufficient room for literally 144,000 to be in the courts of the Temple. Do the math, yourself and figure out how much room we each would have....and let's all pray that we are granted access to His Temple. For no one can enter His New Jerusalem Eternal Temple either, without passing through the literal Gates of PEARL. And the only requirement of our King is that we love Him with all our hearts, and souls, and minds, and bodies. Would you like entry ? Receive Him today for His Salvation)
IHS
David Jay Jordan
Davidjayjordan@yahoo.com
|
|
|
|
Réponse |
Message 7 de 28 de ce thème |
|
Golden Ratio
The golden section is a line segment divided according to the golden ratio: The total length a + b is to the length of the longer segment a as the length of a is to the length of the shorter segment b
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal tothe ratio of the larger quantity to the smaller one. The golden ratio is an irrationalmathematical constant, approximately 1.6180339887.[1] Other names frequently used for the golden ratio are the golden section (Latin: sectio aurea) and golden mean.[2][3][4] Other terms encountered include extreme and mean ratio,[5] medial section,divine proportion, divine section (Latin:sectio divina), golden proportion, golden cut,[6] golden number, and mean of Phidias.[7][8][9] In this article the golden ratio is denoted by the Greek lowercase letter phi (  ) , while its reciprocal, ) , while its reciprocal,  or or  , is denoted by the uppercase variant Phi ( , is denoted by the uppercase variant Phi (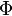 ). ).
Icosahedron Gold nanoparticle viewed in electron microscope.
Our Galena lead was polished following the Golden ratio and so converted into a Gold icosahedron
The ark of the Covenant
Detailed instructions[10] are given by God for the plan of the Ark: it is to be 2½ cubits in length, 1½ in breadth, and 1½ in height (as 21⁄2×11⁄2×11⁄2 royal cubits or 1.31×0.79×0.79 m). Then it is to be plated entirely with gold, and a crown or molding of gold is to be put around it. Four rings of gold are to be put into its four feet—two on each side—and through these rings staves of shittim-wood overlaid with gold for carrying the Ark are to be inserted; and these are not to be removed. A golden cover, adorned with golden cherubim, is to be placed above the Ark.
Although perhaps not immediately obvious, phi and the golden section also appear in the Bible.
|
|
In Exodus 25:10, God commands Moses to build the Ark of the Covenant, in which to hold His Covenant with the Israelites, the Ten Commandments, saying,
"Have them make a chest of acacia wood-
two and a half cubits long,
a cubit and a half wide,
and a cubit and a half high."
|
The ratio of 2.5 to 1.5 is 1.666..., which is as close to phi (1.618 ...) as you can come with such simple numbers and is certainly not visibly different to the eye. The Ark of the Covenant is thus constructed using the Golden Section, or Divine Proportion. This ratio is also the same as 5 to 3, numbers from the Fibonacci series.
In Exodus 27:1-2, we find that the altar God commands Moses to build is based on a variation of the same 5 by 3 theme:
"Build an altar of acacia wood, three cubits high; it is to be square, five cubits long and five cubits wide."
Note: A cubit is the measure of the forearm below the elbow. |
 |
|
Note : Acacia Wood synonym of Bitterness
Noah's Ark uses a Golden Rectangle
|
In Genesis 6:15, God commands Noah to build an ark saying,
"And this is the fashion which thou shalt make it of: The length of the ark shall be three hundred cubits, the breadth of it fifty cubits, and the height of it thirty cubits."
Thus the end of the ark, at 50 by 30 cubits, is also in the ratio of 5 to 3, or 1.666..., again a close approximation of phi not visibly different to the naked eye. Noah's ark was built in the same proportion as ten arks of the covenant placed side by side.
|
|
The Number 666 is related to Phi
|
|
Revelation 13:18 says the following:
"This calls for wisdom. If anyone has insight, let him calculate the number of the beast, for it is a man's number. His number is 666."
|
This beast, regarded by some as the Anti-Christ described by John, is thus related to the number 666, one of the greatest mysteries of the Bible.Curiously enough, if you take the sine of 666º, you get -0.80901699, which is one-half of negative phi, or perhaps what one might call the "anti-phi." You can also get -0.80901699 by taking the cosine of 216º, and 216 is 6 x 6 x 6.
The trigonometric relationship of sine 666º to phi is based on an isosceles triangle with a base of phi and sides of 1. When this triangle is enclosed in a circle with a radius of 1, we see that the lower line, which has an angle of 306º on the first rotation and 666º on the second rotation, has a sine equal to one-half negative phi.
In this we see the unity of phi divided into positive and negative, analogous perhaps to light and darkness or good and evil. Could this "sine" be a "sign" as well?
In addition, 666 degrees is 54 degrees short of the complete second circle and when dividing the 360 degrees of a circle by 54 degrees you get 6.66... The other side of a 54 degree angle in a right angle is 36 degrees and 36 divided by 54 is .666.
Phi appears throughout creation, and in every physical proportion of the human body. In that sense it is the number of mankind, as the mysterious passage ofRevelation perhaps reveals.
|

The Illuminati (plural of Latin illuminatus, "enlightened") is a name given to several groups, both historical and modern, and both real and fictitious. Historically, the name refers specifically to the Bavarian Illuminati, an Enlightenment-era secret society founded on May 1, 1776.
In modern times it is also used to refer to a purported conspiratorial organization which acts as a shadowy "power behind the throne", allegedly controlling world affairs through present day governments and corporations, usually as a modern incarnation or continuation of the Bavarian Illuminati. In this context, the Illuminati are believed to be the masterminds behind events that will lead to the establishment of a New World Order.
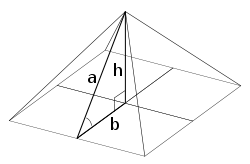 |
A regular square pyramid is determined by its medial right triangle, whose edges are the pyramid's apothem (a), semi-base (b), and height (h); the face inclination angle is also marked. Mathematical proportions b:h:a of  and and 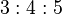 and and  are of particular interest in relation to Egyptian pyramids. are of particular interest in relation to Egyptian pyramids. |
|
|
|
|
Réponse |
Message 8 de 28 de ce thème |
|
|
|
|
Réponse |
Message 9 de 28 de ce thème |
|
The Great Pyramid at the Giza Plateau, Egypt, is mysterious, mystical and strategically placed on the face of the Earth. It is aligned with the four cardinal points more accurately than any other structure, even the Greenwich observatory. The builders displayed enlightened understanding of engineering, mathematics, physics and astronomy. They also had a profound knowledge of the Earth's dimensions. Many scientist and scholars now think it was built earlier than the reign of Cheops (Khufu) at 2600 B.C. They disagree with the traditional view of Egyptologist and attribute it to an advanced civilization before the rule of the Pharaohs. I am convinced they are right. For more details follow the "Egypt/Center of Earth" link.
The Pyramid lies in the center of gravity of the continents. It also lies in the exact center of all the land area of the world, dividing the earth's land mass into approximately equal quarters. It lies in the middle of Egypt and in the middle of Lower and Upper Egypt 
The Plate XX from an original 1877 copy of Piazzi Smyth's "Our Inheritance in the Great Pyramid". Charles Piazzi Smyth (1819-1900) was Astronomer Royal for Scotland and a respected Scientist.
The north-south axis (31 degrees east of Greenwich) is the longest land meridian, and the east-west axis (30 degrees north) is the longest land parallel on the globe. There is obviously only one place that these longest land-lines of the terrestrial earth can cross, and it is at the Great Pyramid! This is incredible, one of the scores of features of this mighty structure which begs for a better explanation.
Pyramid Statistics © 2000 by Larry Orcutt,
A total of over 2,300,000 blocks of limestone and granite were used in its construction with the average block weighing 2.5 tons and none weighing less than 2 tons. The large blocks used in the ceiling of the King's Chamber weigh as much as 9 tons.

Original entrance of the Great Pyramid.
Massive blocks of limestone form a relieving arch over the entrance.
- The base of the pyramid covers 13 acres, 568,500 square feet and the length of each side was originally 754 feet, but is now 745 feet.
- The original height was 481 feet tall, but is now only 449 feet.
The majority of the outer casing, which was polished limestone, was removed about 600 years ago to help build cities and mosques which created a rough, worn, and step-like appearance. The base measurements of the Great Pyramid are: north - 755.43 ft; south - 756.08 ft; east - 755.88 ft; west - 755.77 ft. These dimensions show no two sides are identical; however, the distance between the longest and shortest side is only 7.8 inches. Each side is oriented almost exactly with the four Cardinal points. The following being the estimated errors: north side 2'28" south of west; south side 1'57" south of west; east side 5'30" west of north; and west side 2'30" west of north. The four corners were almost perfect right angles: north-east 90degrees 3' 2"; north-west 89 degrees 59'58"; south-east 89 deg 56'27"; and south-west
90 deg 0'33". When completed, it rose to a height of 481.4 ft., the top 31 feet of which
are now missing. It's four sides incline at an angle of about 51deg. 51 min. with the ground. At its base, it covers an area of about 13.1 acres. It was built in 201 stepped tiers, which are visible because the casing stones have been removed. It rises to the height of a modern 40-story building.
THE BEDROCK AND CORE
The pyramid is built partly upon a solid, large, bedrock core and a platform of limestone blocks which can be seen at the northern and eastern sides. The builder of this pyramid was very wise to choose this site because most of the stones, with the exception of the casing stones, some granite and basalt stones, could be cut right on the spot and in the nearby quarry. This practical choice made it possible to reduce considerably the time and back-breaking labor needed to drag the stones from distant quarries across the Nile.
The many surveys done on the pyramid proved that the Egyptians located the sides of the pyramid along the four Cardinal Points with extreme accuracy. Whether they used the stars, and/or the rising and setting sun, cannot be determined. One this is certain, that whatever method they used was direct and very simple.
Once the sand, gravel and loose rocks had been removed, down to the solid bedrock of the plateau, the whole pyramid site was open-cast quarried into blocks, leaving a square core for the center of the pyramid (the core is approximately 412.7 ft square, and rises approx. 46.25 feet high). These blocks were then stored outside a low wall; made of mortared stone that surrounds the core (the outside dimensions of the wall are approx. 887.3 feet square). Today there still remains the foundation of this wall on the north, south and west sides of the pyramid, at an average distance of 65 feet from the outer edge of the base casing stone.
This core gives the pyramid stability from the downward and horizontal forces that will develop from the superimposed loads of blocks of stones that are piled up, as the pyramid rises. Also, from the prevailing north-west winds that exert enormous pressures on the huge areas of the pyramid's faces, thus increasing these forces further.
Leveling of the entire pyramid site was accomplished by flooding the area inside the wall with water, leaving just the high spots. These them were cut down to the level of the surface of the water. Next, some of the water was released and the high spots again were cut down to the water's surface. This
process was repeated until the entire pyramid site, between the core and the four walls, was leveled down to the base of the pyramid's platform.
THE CASING STONES
A few of the fine limestone casing blocks remain at the base of the northern side and show how accurately the stones were dressed and fitted together. The core masonry, behind the casing stones, consists of large blocks of local limestone, quarried right on the spot, built around and over the
bedrock core. The size of this core cannot be determined, since it is completely covered by the pyramid.
The casing stones were of highly polished white limestone, which must have
been a dazzling sight. Unlike marble, which tends to become eroded with time
and weather, limestone becomes harder and more polished.
THE SIZE OF THE BLOCKS
The size of the blocks are based on a chance discovery in 1837 by Howard Vyse. He found two of the original side casing blocks at the base of the pyramid, 5 ft x 8 ft x 12 ft, with an angle of 51 degrees, 51 minutes cut on one of the 12 ft. sides. Each of these stones weighed (5 x 8 x 12)/2000 =
39.9 tons before the face angle was cut. These originally were used for the side casing stones of Step No. 1, in the Pascal computer program. The sizes of all the other blocks were scaled from these two original blocks of the remaining Steps 2 to 201.
THE GREAT PYRAMID'S DIMENSIONS AND THEIR LAYOUT
One acre = 43,560 sq. ft, or 208.71 feet on a side.
For the pyramid's base, length = width = (square root of 13.097144 acres) x
208.71 feet = 755.321 feet. Or 755.321 x 12 = 9063.85 inches.
Height = (755.321 x tangent 51deg 51 min)/2 = 480.783 feet. Or 480.783 x 12
= 5769.403 inches.
For the cap stone base: length = width = (32.18 x 2)/tangent 51deg 51 min =
50.55 inches.
The average size of a pyramid stone = (5 x 8 x 12)
The average side measurement, at the base = 759.3 ft.
The height used was 201 steps high, or 480 feet. (This is minus the height
of the Capstone, which was one piece in itself. Geometry of the Great Pyramid
DIMENSIONS of Great Pyramid
|
|
|
|
|
Réponse |
Message 10 de 28 de ce thème |
|
The following article is Copyright © 2001-2003 aiwaz.net_institute.
If the calculations concerning the royal cubit are correct the main dimensions of the pyramid should also prove that. The approximate dimensions of the pyramid are calculated by Petrie according to the remains of the sockets in the ground for the casing stones whose remains are still at the top of the pyramid, and the angle 51° 52' ± 2' of the slopes. The base of 9069 inches is approximately 440 royal cubits (the difference is 9 inches which is not a remarkable difference if we consider the whole dimension and consider that the employed data represent only an estimation of the real values) whereas the calculated height, 5776 inches, is precisely 280 royal cubits. The relation 440:280 can be reduced to 11:7, which gives an approximation of the half value of Pi.
Squaring the Circle

The circle and the square are
united through the circumference:
440x4=1760=2x22/7x280
area of square: 440x440=193600
area of circle:28x28x22/7=246400
sum: 440000
|
The engagement of Pi value in the main dimensions suggests also a very accurate angle of 51° 52' ± 2' of the slopes which expresses the value of Pi. Another coincidence is the relation between the height of the pyramid's triangle in relation to a half of the side of the pyramid, since it appears to be the Golden Section, or the specific ratio ruling this set of proportions, F = (sqr(5)+1)/2 = 1.618 = 356:220. This ratio, 356:220 = 89:55 is also contained in the first of Fibonacci Series:
1 2 3 5 8 13 21 34 55 89 144 ...
A single composition contains two apparently contradicting irrational numbers P and F, without disrupting each other. This appears to be completely opposed to the classical architectural canon which postulates that in 'good' composition no two different geometrical systems of proportions may be mixed in order to maintain the purity of design. But analysis of other architectural and artistic forms suggested that the greatest masters skillfully juggled the proportional canons without losing the coherent system, for they knew that these systems can be interconnected if the path that links them is found. That is obvious In the case of the Great Pyramid where two different principles are interweaved without interference ruling different angles of the composition, which is most importantly a most simple one, namely 11:7, a most simple ratio obviously signifying such infinite mysteries as the value of P and most 'natural' value of F. In spite of common miss-understanding of architectural composition, the most mysterious and praised compositions are very simple but not devoid of anthropomorphic appeal, since everything is made out of human proportions, just like Vitruvius describing the rations of the human body, very simple and very clean. The numbers 7 and in 11 are successive factors in the second of Fibonacci progressions that approximate geometry of the pentagram:
1 3 4 7 11 18 29 47 76 123 ...
The summary of the selected main mean dimensions is:
|
dimension
|
b. inch
|
m
|
royal cub.
|
palm
|
digit
|
|
base
|
9068.8
|
230.35
|
440
|
3,080
|
12,320
|
|
height
|
5776
|
146.71
|
280
|
1,960
|
7,840
|
|
sum
|
|
|
720
|
|
20,160
|
|
slope
|
7343.2
|
186.52
|
356
|
2,492
|
9,968
|
|
edge
|
8630.4
|
219.21
|
418
|
2,926
|
11,704
|

The main source of all kinds of delusions and speculations about our mythical past for the western man comes of course from Plato. With the myth of Atlantis he planted the necessary seed of mythical Eden, a culture of high intelligence that lived before the known history. If Plato received any wisdom from the ancient Egypt it could perhaps be traced in the canon of numbers that is so latently present throughout his work, but never on the surface. This canon seems to appear in the descriptions of his fantastic cities where everything is most carefully calculated and proportioned. The topic of Plato's Laws is the description of the ideal state called Magnesia which is entirely composed out of the mysterious number 5,040.
The distance* when Earth is closest to Sun (perihelion) is 147x106 km, which is translated into royal cubits 280x109, hinting at the height of the Great pyramid,
280 royal cubits
The Golden Ratio & Squaring the Circle in the Great Pyramid
A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less. [Euclid]
The extreme and mean ratio is also known as the golden ratio.

If the smaller part = 1, and larger part = G, the golden ratio requires that
G is equal approximately 1.6180
Does the Great Pyramid contain the Golden Ratio?
Assuming that the height of the GP = 146.515 m, and base = 230.363 m, and using simple math we find that half of the base is 115.182 m and the "slant height" is 186.369 m
Dividing the "slant height" (186.369m) by "half base" (115.182m) gives = 1.6180, which is practically equal to the golden ration!
The earth/moon relationship is the only one in our solar system that contains this unique golden section ratio that "squares the circle". Along with this is the phenomenon that the moon and the sun appear to be the same size, most clearly noticed during an eclipse. This too is true only from earth's vantage point…No other planet/moon relationship in our solar system can make this claim.
If the base of the Great Pyramid is equated with the diameter of the earth, then the radius of the moon can be generated by subtracting the radius of the earth from the height of the pyramid (see the picture below).

Also the square (in orange), with the side equal to the radius of the Earth, and the circle (in blue), with radius equal to the radius of the Earth plus the radius of the moon, are very nearly equal in perimeters:
Orange Square Perimeter = 2+2+2+2=8
Blue Circle Circumference = 2*pi*1.273=8
Note:
Earth, Radius, Mean = 6,370,973.27862 m *
Moon, Radius, Mean = 1,738,000 m.*
Moon Radius divided by Earth Radius = 0.2728 *
* Source: Astronomic and Cosmographic Data
Let's re-phrase the above arguments **

In the diagram above, the big triangle is the same proportion and angle of the Great Pyramid, with its base angles at 51 degrees 51 minutes. If you bisect this triangle and assign a value of 1 to each base, then the hypotenuse (the side opposite the right angle) equals phi (1.618..) and the perpendicular side equals the square root of phi. And that’s not all. A circle is drawn with it’s centre and diameter the same as the base of the large triangle. This represents the circumference of the earth. A square is then drawn to touch the outside of the earth circle. A second circle is then drawn around the first one, with its circumference equal to the perimeter of the square. (The squaring of the circle.) This new circle will actually pass exactly through the apex of the pyramid. And now the “wow”: A circle drawn with its centre at the apex of the pyramid and its radius just long enough to touch the earth circle, will have the circumference of the moon! Neat, huh! And the small triangle formed by the moon and the earth square will be a perfect 345 triangle (which doesn’t seem to mean much.) |
|
|
|
Réponse |
Message 11 de 28 de ce thème |
|
Was the golden ratio intentionally built into the Great Pyramid of Cheops?
Why would anyone intentionally build the golden ratio into a pyramid, or other structure? What was the significance of to the Egyptians? And did the ancient Egyptians intentionally design the Great Pyramid to square the circle?
The answer to these questions is uncertain since designing the Great Pyramid according to the simple rules explained by the graphic below would give the pyramid automatically (by coincidence? ) all its "magic" qualities.
The height of the Great Pyramid times 2π exactly equals the perimeter of the pyramid. This proportions result from elegant design of the pyramid with the height equal two diameters of a circle and the base equal to the circumference of the circle. Click here or on the image below to see larger picture.



For the angle of the Great Pyramid, any theory of the base, combined with any theory of the height, yields a theoretic angle; but the angles actually proposed are the following** :
|
Angle of casing measured
By theory of 34 slope to 21 base
Height : circumference :: radius to circle
9 height on 10 base diagonally
7 height to 22 circumference
area of face = area of height squared
(or sine) = cotangent, and many other relations)
2 height vertical to 3 height diagonal
5 height on 4 base
|
51º 52' ± 2' (51.867)
51º 51' 20"
51º 51' 14.3"
51º 50' 39.1"
51º 50' 34.0"
51º 49' 38.3"
51º 40' 16.2"
51º 20' 25"
|
** Page 184, The Pyramids and Temples of Gizeh
by Sir W.M.Flinders Petrie 1883
Comparing the Great Pyramid with the Pyramid of the Sun in Teotihuacan
The Pyramid of the Sun and the Great Pyramid of Egypt are almost or very nearly equal to one another in base perimeter. The Pyramid of the Sun is "almost" half the height of the Great Pyramid. There is a slight difference. The Great Pyramid is 1.03 - times larger than the base of the Pyramid of the Sun. Conversely, the base of the Pyramid of the Sun is 97% of the Great Pyramid's base.

The ratio of the base perimeter to the height:
| Great Pyramid |
Pyramid of the Sun |
6.2800001... : 1
(deviates by 0.05 % from the
6.2831853 value for 2 x pi) |
12.560171... : 1
(deviates by 0.05 % from the
12.566371 value for 4 x pi) |
The Great Pyramid - Metrological Standard
The Great Pyramid is generally regarded as a tomb and as grandiose memorial to the pharaoh who commissioned it. The opposing view is that of the pyramid being the culminating achievement of those who practiced an advanced science in prehistory.
The Great Pyramid is a repository of universal standards, it is a model of the earth against which any standard could be confirmed and corrected if necessary.
It is exactly the imperishable standard, which the French had sought to create by the devising of the metre, but infinitely more practical and intelligent.
From classical times, the Great pyramid has always been acknowledged as having mathematical, metrological and geodetic functions. But ancient Greek and Roman writers were further removed in time from the designers of the Great Pyramid than they are from us. They had merely inherited fragments of a much older cosmology; the science in which it was founded having long since disappeared.
The Concave Faces of the Great Pyramid

Aerial photo by Groves, 1940 (detail).
In his book The Egyptian Pyramids: A Comprehensive, Illustrated Reference, J.P. Lepre wrote:
One very unusual feature of the Great Pyramid is a concavity of the core that makes the monument an eight-sided figure, rather than four-sided like every other Egyptian pyramid. That is to say, that its four sides are hollowed in or indented along their central lines, from base to peak. This concavity divides each of the apparent four sides in half, creating a very special and unusual eight-sided pyramid; and it is executed to such an extraordinary degree of precision as to enter the realm of the uncanny. For, viewed from any ground position or distance, this concavity is quite invisible to the naked eye. The hollowing-in can be noticed only from the air, and only at certain times of the day. This explains why virtually every available photograph of the Great Pyramid does not show the hollowing-in phenomenon, and why the concavity was never discovered until the age of aviation. It was discovered quite by accident in 1940, when a British Air Force pilot, P. Groves, was flying over the pyramid. He happened to notice the concavity and captured it in the now-famous photograph. [p. 65] |
|
|
|
Réponse |
Message 12 de 28 de ce thème |
|
This strange feature was not first observed in 1940. It was illustrated in La Description de l'Egypte in the late 1700's (Volume V, pl. 8). Flinders Petrie noticed a hollowing in the core masonry in the center of each face and wrote that he "continually observed that the courses of the core had dips of as much as ½° to 1°" (The Pyramids and Temples of Gizeh, 1883, p. 421). Though it is apparently more easily observed from the air, the concavity is measurable and is visible from the ground under favorable lighting conditions.

Ikonos satellite image of the Great Pyramid.
Click to view larger image.
I.E.S. Edwards wrote, "In the Great Pyramid the packing-blocks were laid in such a way that they sloped slightly inwards towards the centre of each course, with a result that a noticeable depression runs down the middle of each face -- a peculiarity shared, as far as is known, by no other pyramid" (The Pyramids of Egypt, 1975, p. 207). Maragioglio and Rinaldi described a similar concavity on the pyramid of Menkaure, the third pyramid at Giza. Miroslav Verner wrote that the faces of the Red Pyramid at Dahshur are also "slightly concave."

Diagram of the concavity (not to scale).
What was the purpose for concave Grea the first pyramid should hold true for the others."

Three proposed "baselines" of the Great Pyramid (not to scale).
The purpose for the concavity of the Great Pyramids remains a mystery and no satisfactory explanation for this feature has been offered. The indentation is so slight that any practical function is difficult to imagine.
© 2000 by Larry Orcutt, Catchpenny Mysteries, Reprinted with permission
The Great Pyramid's "Air Shafts"
While shafts in the King's Chamber had been described as early as 1610, the shafts in the Queen's Chamber were not discovered until 1872. In that year, Waynman Dixon and his friend Dr. Grant found a crack in the south wall of the Queen's Chamber. After pushing a long wire into the crack, indicating that a void was behind it, Dixon hired a carpenter named Bill Grundy to cut through the wall. A rectangular channel, 8.6 inches wide and 8 inches high, was found leading 7 feet into the pyramid before turning upward at about a 32º angle. With the two similar shafts of the King's Chamber in mind, Dixon measured a like position on the north wall, and Grundy chiseled away and, as expected, found the opening of a similar channel. The men lit fires inside the shafts in an attempt to find where they led. The smoke stagnated in the northern shaft but disappeared into the southern shaft. No smoke was seen to exit the pyramid on the outside. Three artifacts were discovered inside the shafts: a small bronze grapnel hook, a bit of cedar-like wood, and a "grey-granite, or green-stone" ball weighing 8.325 grains thought to be an Egyptian "mina" weight ball.
Shafts and passages of the Great Pyramid at Giza.
The Shafts of the Queen's Chamber Described
The openings of both shafts are located at the same level in the chamber, at the joint at the top of the second course of granite wall-stone; the ceilings of the shafts are level with the joint.
The northern shaft runs horizontally for just over six feet (76"), then turns upward at a mean angle of 37º 28'. The shaft terminates about 20 feet short of the outside of the pyramid. The total length of the northern shaft is about 240 feet and rises at an angle of 38º for the majority of its length.
The southern shaft also runs horizontally for just over six feet (80"), then turns upward at a mean angle of 38º 28'. The total length of the southern shaft is about 250 feet and, as its northern counterpart, ascends at an angle of 38º for the majority of its length and comes to an end about 20 feet short of the outside of the pyramid.
The Shafts of the King's Chamber Described
The openings of both shafts are located at roughly the same level in the chamber, at the joint at the top of the first course of granite wall-stone. The northern opening is slightly lower, its ceiling being level with the joint, while the floor of the southern opening is roughly level with the joint.
The northern shaft is rectangular, about 7 inches wide by 5 inches high, a shape it maintains throughout its length. The shaft begins on the horizontal for about 6 feet then takes a series of four bends. While maintaining its general upward angle, it shifts first to the north-northwest then back to north, then to north-northeast, and finally back to true north. It has been speculated by some that this unexplained semicircular diversion might have been necessary to avoid some heretofore undiscovered feature of the pyramid. The total length of the northern shaft is about 235 feet and rises at an angle of 31º (with a variation of between 30º 43' and 32º 4') for the majority of its length.
Though the first eight feet of the northern shaft is intact, the next thirty or so feet have been excavated by treasure seekers, presumably following the direction of the shaft in search of treasure. The breach to the shaft was made in the west wall of the short passage leading from the antechamber to the King's Chamber. A modern iron grate today guards the mouth of this breach.
The southern shaft is different in appearance. Its mouth is larger, about 18" wide by 24" high. The dimensions are reduced to about 12" by 18" within a few feet, and then narrows yet more to about 8" by 12". The shape is not rectangular, as is the northern shaft, but has a dome shape where it enters the chamber, with a narrow floor, the angle of the walls being slightly obtuse, and a dome-shaped ceiling. The shaft is horizontal and true south for about 6 feet. At the first bend, its shape changes to an oval, and continues thusly for about 8 feet. Its orientation also changes slightly from true south to south-southwest. At the second bend its shape changes yet again to a rectangle, with a height greater than its width. It retains this shape for the 160 feet to the outside of the pyramid where it emerges at the 101st course of stone. It also changes directions once again at the second bend to a more severe south-southwest diversion. The total length of the southern shaft is about 175 feet and ascends at an angle of 45º (with a variation of between 44º 26' and 45º 30') for the majority of its length.
The Function of the Shafts
When Sandys described the Great Pyramid in 1610, he wrote of the shafts:
In the walls, on each side of the upper room, there are two holes, one opposite to another, their ends not discernable, nor big enough to be crept into -- sooty within, and made, as they say, by a flame of fire which darted through it.
Greaves also wrote of the King's Chamber shafts in 1638. Considering the presence of the lampblack inside, he concluded that the shafts had been intended as receptacles for an "eternal lamp." In 1692, M. Maillet wrote that the shafts served as means of communication for those who were buried alive with the dead king. Not only did the shafts provide air, he reasoned, but they also provides a passage for food which was placed in boxes and pulled through by rope.
By the 20th century, the shafts were presumed to have been designed to provide ventilation. That view has slowly been changing, however. I.E.S. Edwards wrote, "The object of these shafts is not known with certainty; they may have been designed for the ventilation of the chamber or for some religious purpose which is still open to conjecture." (The Pyramids of Egypt, 1961, p. 126.) Ahmed Fakhry wrote, "They are usually referred to as 'air channels,' but most Egyptologists believe that they had a religious significance related to the soul of the king." (The Pyramids, 1969, p. 118.) More recently, Mark Lehner wrote:
A symbolic function should also be attributed to the so-called "air-shafts," which had nothing to do with conducting air. No other pyramid contains chambers and passages so high in the body of masonry as Khufu's and so the builders provided the King's Chamber with small model passages to allow the king's spirit to ascend to the stars. (The Complete Pyramids, 1997, p. 114)
There are many reasons why it is not likely that the shafts were meant for ventilation. The complex angles of the shafts necessitated the piercing of many courses of stone, a daunting logistical challenge during design and construction. Horizontal shafts would have been much easier to build: shafts carved through a single course of stone. One might well wonder why ventilation would be needed at all! No other known pyramid builder made such provisions; even workers in rock-cut tombs managed on the air provided solely by the entrance passage. When the bulk of work on the King's Chamber was being done, ambient air was plentiful as the ceiling had not yet been put in place. The chamber was finished as the superstructure rose.
There are also, however, reasons why it is not likely that the shafts were meant to serve as "launching ramps" for the king's ka. When, in 1964, Alexander Badawy and Virginia Trimble determined that the shafts are "aimed" at certain "imperishable" circumpolar stars and at the constellation of Orion, the function of the shafts as cultic features seemed certain. But the ka did not require a physical means of egress from a tomb -- false doors served this purpose quite nicely both before and after Khufu's reign. The passage that ascends to the entrance of the pyramid is also directed at the circumpolar stars in the manner of previous pyramids. The northern shafts for such a use would have been a needless and bothersome redundancy, although admittedly the Egyptians were not adverse to redundancies.
That fact that no other pyramid in Egypt is known to posses similar shafts as those of the Great Pyramid is problematic. If the shafts were so important for either ventilation or as passages for the king's ka, then why were they omitted in other funerary structures? It is obvious that the builders of Khufu's pyramid went to a jolly lot of trouble to incorporate the shafts into the design of the pyramid, but the true reason why still remains a mystery.
http://genesis.allenaustin.net/pyramid.htm |
|
|
|
Réponse |
Message 13 de 28 de ce thème |
|
Le nombre 666 étant défini comme nombre de la Bête, se trouve en Apocalypse 13/18!
|
666 =
|
[6] 3 + [6] 3 + [6] 3
|
|
| |
216 + 216 + 216
|
= 648 |
|
648 =
|
[6] 3 + [4] 3 + [8] 3
|
|
| |
216 + 64 + 512
|
= 792 |
|
792 =
|
[7] 3 + [9] 3 + [2] 3
|
|
| |
343 + 729 + 8
|
= 1080 |
|
1080 =
|
[1] 3 + [0] 3 + [8] 3 + [0] 3
|
|
| |
1 + 0 + 512 + 0
|
= 513 |
|
513 =
|
[5] 3 + [1] 3 + [3] 3
|
|
| |
125 + 1 + 27
|
= 153 |
| 153 = |
[1] 3 + [5] 3 + [3] 3
|
|
| |
1 + 125 + 27
|
= 153... |
|
|
|
 Premier
Premier
 Précédent
2 a 13 de 28
Suivant
Précédent
2 a 13 de 28
Suivant Dernier
Dernier
|

