|
جواب |
رسائل 1 من 271 في الفقرة |
|
22 de TISHRI=22/7=3.14
22/7=DIA DE MARIA MAGDALENA
EN EL OCTAVO DIA DE LA FIESTA DE LOS TABERNACULOS, OSEA EL 22 DE TISHRI O 22/7 (LEVITICO 23:33)
|
|
|
 أول أول
 سابق
257 إلى 271 من 271
لاحق سابق
257 إلى 271 من 271
لاحق
 آخر
آخر
|
|
جواب |
رسائل 257 من 271 في الفقرة |
|
|
|
|
جواب |
رسائل 258 من 271 في الفقرة |
|
|
|
|
جواب |
رسائل 259 من 271 في الفقرة |
|
|
|
|
جواب |
رسائل 260 من 271 في الفقرة |
|
Was the metre invented by the Ancient Egyptians 4500 years ago?
One of our readers, John Frewen-Lord, speculates that the metre may be the modern version of a measure that was familiar to the Pharaohs.
While we think of today’s metric system (SI) as mostly a modern invention (1960), we have been led to believe for many years now that its most fundamental base unit, the metre, originated in France in 1793, and represented one ten-millionth of the earth’s quadrant (the distance from the earth’s equator to the North Pole, as measured at sea level) . Yet just a few years ago, the late Pat Naughtin discovered that the proposal for a universal standard of length very close to the metre may in fact have originated much earlier, via Bishop John Wilkins, an English cleric and philosopher, and a member of the Royal Society, in the mid-1600s. Recent comments on Metric Views now bring even that assertion into doubt, with the discovery of a measuring device called the wand having been around much longer still.
It is known that the wand, divided into ten segments, was almost exactly, to within a few millimetres, the same length as today’s metre, and that it was used as long as 1000 years ago. But what if all these versions of the metre were simply the rediscovery (or the handing down over time) of a standard measure, equating to the metre, that was invented in Egypt over 4500 years ago?
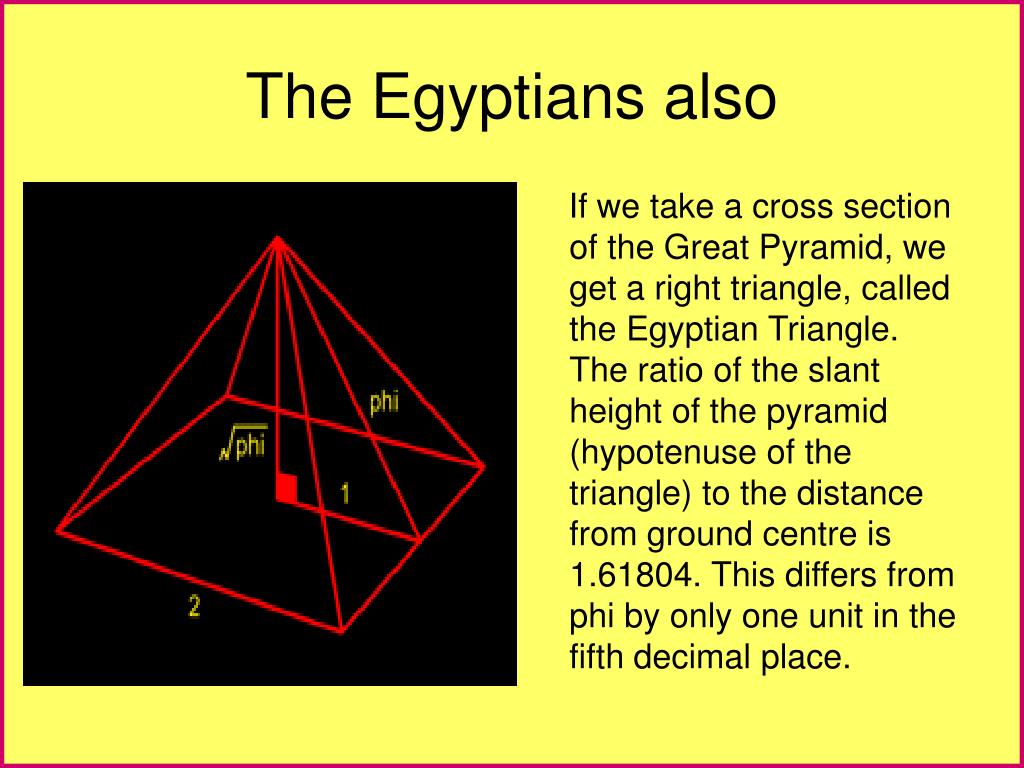
When we think of units of measure used in Biblical times, the cubit usually springs to mind. In fact, opponents of metric conversion have often referred to the cubit, in jest at least, as having as much validity as the metre. Such people should be careful for what they wish for, for, as we shall see, the cubit and the metre may in fact be directly related – and remarkably both are directly traceable to the Great Pyramid at Giza.
At first sight, such direct relationship may not be immediately apparent. There are a number of variations of the cubit, each different in length, but it is accepted that the Egyptian royal cubit is the definitive cubit, of which a physical example is on display in the Liverpool museum. Used to set out the Great Pyramid, its length measures 524 mm, or 0.524 m. For anyone hoping to see a nice round relationship between the cubit and the metre, I’m afraid the story is much more complicated than that! But keep in mind that number of 0.524 – for it will crop up again.
Let us look briefly at some of the mathematical properties of the Great Pyramid. Apart from the fact that it is just 3/60ths of a degree off an orientation of true north (the Prime Meridian through Greenwich is 9/60ths of a degree out of such an alignment), the Great Pyramid contains some quite stunning dimensional relationships between the numerical constants of pi (?), phi (?) and Phi (?) – and those relationships involve a dimension that is exactly equal to today’s metre. Let us explore this a bit further.
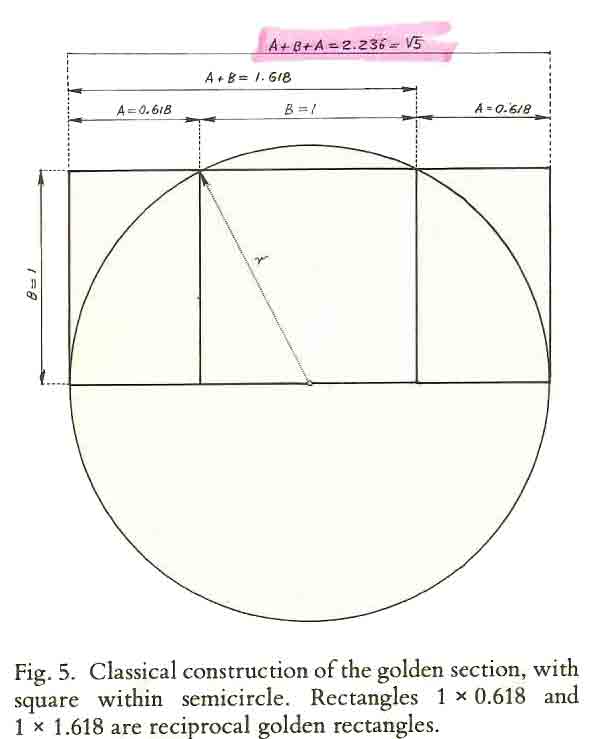
We all know what pi is. It is the ratio of a circle’s circumference to its diameter, and is approximately equal to 3.1416 (another number to keep in mind). We are probably less familiar with Phi and phi. One is the reciprocal of the other, with values of 1.618 and 0.618 respectively. The value of 1.618 is known as Phi with a capital P (?), while the reciprocal 0.618 value is represented by the lower case phi (?), and the two collectively are known by many names, such as the Golden Ratio, the Golden Mean, the Golden Number, and others, but they are values that exist throughout nature. Their discovery is attributed to mathematician Fibonacci in the 13th century.
Fibonacci noted that much of nature – and indeed much of Roman architecture – encompassed relationships of 1.618 and 0.618 for various aspects of design, and that these relationships relate to what is known as the Fibonacci sequence, consisting of 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, and so on, where each number is the sum of the previous two numbers. What is not always realised is that if you take any two adjacent numbers, say 55 and 89, you can obtain two ratios – 1.618 if you divide the second by the first, and 0.618 if you divide the first by the second (the minor variations in the decimal places get smaller as the numbers get bigger, coinciding at infinity). The Golden Ratio has a few unique properties – in fact these equations work only with the Golden Ratio and nothing else:
? = 1 + ? (i.e. 1.618 = 1 + 0.618);
? = 1/? (i.e. 1.618 = 1 ÷ 0.618);
? + 1 = ?² (i.e. 1.618 + 1 = 1.618² = 2.618);
? – 1 = 1/? (i.e. 1.618 – 1 = 1 ÷ 1.618 =0.618).
If we skip alternate numbers in the Fibonacci sequence, we end up with the same result as either ?² or adding 1 to ? – e.g. 144 ÷ 55 = 2.618 = 1.618 + 1 = 1.618² (keep in mind also the number of 2.618). Now you may be saying that this is all very interesting, but what has it got to do with the Great Pyramid at Giza, let alone the origins of the metre? All will become clear!
It is well known and accepted that the Great Pyramid incorporates the value of ? in its geometry – this was discovered by Englishman John Taylor in 1859, when he found that if you divide half the length of the Pyramid’s base perimeter by its height, you end up with ?. The base length of one side is 230.3 m, while its original height is 146.6 m. Therefore (230.3 x 2) ÷ 146.6 = 3.1418 – not precisely ?, but then the height of 146.6 m is at best an estimate of just how high the Pyramid was 4500 years ago (the very top is now missing, as is part of its external cladding, and ground level has likely changed). Likewise, take a circle with the same circumference as the perimeter of the base of the Great Pyramid. Calculate the radius of this circle. It will be found to be exactly equal to the Great Pyramid’s height (230.3 x 4 = 921.2. 921.2 ÷ (2 x 3.1416) = 146.6).
We must note that these relationships, along with many other relationships embodied in the Great Pyramid, can be made using any measurement units – they are not exclusive to the metre.
The Golden Ratio ? is there as well. If we take the surface area of the four sides, and divide that by the area of the base, we come to the value of ? (4 x 0.5 x 230.3 x 186.4 ÷ 230.3² = 1.618). Again, that is purely a ratio, and is not dependent upon any particular unit of measure. But now let us do some more calculations involving the Great Pyramid’s geometry that are dependent upon the metre – and only the metre.
- If we add two of the sides of the Pyramid’s base together, then subtract the height, we end up with a rounded value of 100 x ? (230.3 x 2 – 146.6 = 314.0).
- The King’s Chamber measures 5.24 m x 10.47 m. The Chamber’s perimeter = 10 x ? (31.42 m). There are also many measurements in the King’s Chamber that relate to even multiples of ?, but only using metres.
- If we draw two circles, one circumscribing the Pyramid’s base (i.e. intersecting the four corners) and one inside (i.e. touching the mid-point of each side), then subtract, in metres, the circumference of the inner circle from that of the outer circle, you end up with a figure of 299.71. This is almost exactly one millionth of the speed of light in metres per second (299 792 458 m/s – the slight discrepancy is due to rounding at various points along the way).
Hold on – the ancient Egyptians may have known about the metre, but surely they didn’t know about the second? Perhaps they did. The length of two sides of the base of the Great Pyramid is the distance a point on the equator moves through space in exactly one second.
I’m sure if you tried hard enough, the Great Pyramid may be found to contain some mathematics that support imperial measures, even though things like the foot and inch were not anywhere near close to existence 4500 years ago, and anyway are promoted as being based on human properties, not mathematical ones. But there is one thing that really does indicate that the ancient Egyptians were very familiar with the metre. I mentioned early on in this article that the cubit, which was used to build the Great Pyramid (each side has a length of 440 cubits), was 0.524 m long, an apparently odd relationship to the metre. Let us however look at three equations:
- One sixth of ? is 0.5236 – to all intents and purposes exactly the length of the cubit in metres (to within 0.4 mm of the known physical example, and even that assumes that this example’s stated length has not been rounded to three decimal places); quite why one sixth is not clear, but the Great Pyramid is located exactly 30° above the equator – i.e. one sixth of the distance between the two poles.
- One fifth of ?² (2.618) = 0.5236 – again, exactly the length of the cubit in metres. There are five increments of 72° in a circle of 360°. It is known that the earth wobbles slightly on its axis, at the rate of 1° every 72 years.
- ? – ?² (3.1416 – 2.618) = 0.5236 – another relationship that yields the length of the cubit in metres, and ties together, by means of the cubit (and hence the metre), the two constants that are embedded in the Great Pyramid’s mathematical properties.
These equations cannot be pure chance or coincidence, but must have been created by a society that knew all about the metre 4500 years ago, and from which they derived the cubit. One thing is certain – no measurement unit can be more natural than the metre, based as it is on nature’s constants of ? and ? (not to mention the circumference of the earth). Clever people, those ancient Egyptians.
[Note: I claim little original material in this article, but have made extensive use of sources from Wikipedia, YouTube and others, all of which must be treated with the usual caution as to their absolute accuracy. J F-L]
https://metricviews.uk/2013/06/07/was-the-metre-invented-by-the-ancient-egyptians-4500-years-ago/ |
|
|
|
جواب |
رسائل 261 من 271 في الفقرة |
|
|
|
|
جواب |
رسائل 262 من 271 في الفقرة |
|
|
|
|
جواب |
رسائل 263 من 271 في الفقرة |
|
|
|
|
جواب |
رسائل 264 من 271 في الفقرة |
|
|
|
|
جواب |
رسائل 265 من 271 في الفقرة |
|
|
|
|
جواب |
رسائل 266 من 271 في الفقرة |
|
Did you know there are eight Statue of Liberty replicas in Paris?

Here’s the inside guide for how to find all the Statue of Liberty replicas in Paris. Note: One of the liberties is on loan to the US, so technically there are only seven.
First: a lightning quick guide for those who don’t know: The Statue of Liberty was designed by French sculptor Frédéric Auguste Bartholdi and constructed by Gustave Eiffel (yes, the man who made the Eiffel Tower). Liberty was gifted the to US by the French in the late 1880s.
So, here’s where to find the Liberty statues in Paris (and beyond).
The podcast episode
Here’s a quick explainer of it all in podcast form, plus some info about our grand plans to find them all Live on YouTube for July 4th, 2024.
The interactive map
Now, here’s an interactive map of all the Liberty statues to help you find them.
1. The biggest
The grandest replica of all is just off the Grenelle Bridge on the little man-made island called Île aux Cygnes. That’s it pictured above (and below). While Liberty in New York was a gift from the French, this statue in Paris was a gift from the Americans in Paris. And it’s the biggest too, at 11.50 metres (37 feet 9 inches) – which is exactly a quarter as big as the one in New York.

2. The hardest to find
There’s a Liberty nestled in the Jardin de Luxembourg in the sixth arrondissement. You can find it on the western edge of the park. Here’s what it looks like today. It’s just one of many, many statues in the park, so you’re forgiven if you can’t find her straight away.

3. The most prestigious
Head inside the famed Musee d’Orsay on the Left Bank to find this Liberty, which is located in the grand central aisle on the ground floor.
In fact, if you want an in-depth history of Lady Liberty and France, head over to the Musee d’Orsay’s site for much more information.

Subscribe to the Earful Tower newsletter
Want more from Paris? Sign up for the free Earful Tower newsletter, which we send out every Friday through Substack.
4 and 5. The closest two Lady Libs
If you want a two-for-one deal, head to the Arts-et-Metiers museum in the third arrondissement. There’s a Liberty replica right out the front of the building (well, not anymore… it’s on loan to the US). And if you head inside the museum, there’s another perched atop a display in the centre of the main hall.
 
6. The smallest
You’ll have to look very closely for this one. First you’ve got to find the 5m tall statue called Le Centaure at 2 Place Michel Debré in the 6th arrondissement. It was made by French artist César in 1985 and depicts a centaur. And emerging from the breastplate of this centaur you might be able to see a tiny liberty poking out! Full statue followed by a closeup:
 
7. The private Liberty
A listener alerted me to this one and it’s inside a private building. But, if you ever happen to have business at 5 rue du Cirque in the 8th you’ll see a sizeable Liberty in the lobby. Here’s a closer look.

8. The floatiest
There’s an EIGHTH Liberty on top of a péniche by the Eiffel Tower. Who’d have thought? Here’s a pic via my Instagram account (go follow for much more from Paris).
https://theearfultower.com/2024/07/01/did-you-know-there-are-five-statue-of-liberty-replicas-in-paris/ |
|
|
|
جواب |
رسائل 267 من 271 في الفقرة |
|
|
|
|
جواب |
رسائل 268 من 271 في الفقرة |
|
Actually, this is the Templar cross:
And this is the Swiss flag:
|
|
|
|
جواب |
رسائل 269 من 271 في الفقرة |
|
|
|
|
جواب |
رسائل 270 من 271 في الفقرة |
|
According to Pythagoras an entity is called a number when the product of itself is greater than the sum of itself. One is not a number, according to the above definition, it is god, generator of numbers. Two is also not a number, because both the product and the sum are equal to each other, that is, it is a coexisting god, a second generator of numbers. The numbers start with three because 3 X 3 = 9 an

The Tetraktys is the Essence of Teaching and the Sacred Symbol of the Pythagoreans. It consists of the first ten numbers (1-10) arranged in four rows (one in the first row, two in the second, three in the third and four in the fourth row) as shown in the picture. Tetraktyn was called “Tetradas”[1] which in Pythagorean Philosophy is the essence and meaning of the number four. Tetraktys is the fourth “triangular number”[2] thus showing another view of the relationship of Tetrad and Tetraktyos. In any case, we should not forget the relation of Tetraktys with “Ten”. From this the Tetraktys is mentioned according to Iamblichus with the prepositional names: Cosmos (decoration, ornament), Pan (the god Panas – Pan = All), Uranus, Atlas, Key, Aion, Memory, Gnomon, Eimarmene, Kratos, Phanis, Helios, Pythmen et al. By studying the concepts of numbers found in the Tetractyn and their relationships, the Pythagoreans argue that one reaches the attainment of wisdom.
The main relationship of Tetrad and Tetraktyos can also be seen from the famous relationship of the first four numbers with the ten they produce when added (1+2+3+4=10). From these first four numbers (1, 2, 3 & 4), it is possible to construct the ratios: “by four” (4:3, fourth), “by five” (3:2, fifth), “by all ” (2:1, Octave), which attribute to music the mentioned harmonic musical intervals which Pythagoras was the first to precisely determine with numerical reasons. These proportions create Harmony, which for the Pythagoreans has a literally cosmic meaning (hence its name “Cosmos”). The Pythagoreans used the Tetraktyn to swear, even invoking Pythagoras as a god, as can be seen from the “Golden Epics” where it is stated:
“Yes, with the immortal soul, delivered four times
always of a permanent nature.”
(yes, but the one who delivered to our soul the tetractyn,
which is the source of eternal nature.)
Numbers are related to geometric shapes. Thus the unit is related to the point, the dyad to the line, the triad to the triangle, and the tetrad or tetraktys to the tetrahedron (or triangular pyramid), the first geometric solid. Its symbol was considered the square which was also the symbol of the divine and perfection.[5]. Also wisdom was considered to be acquired from the four esoteric sciences for the Pythagoreans of arithmetic, music, geometry and astronomy. It is a symbol of God Apollo and the Pythagoreans connect the Tetraktyn with the Oracle of Delphi, as seen in the important “hearing” about existence mentioned by Iamblichus[6]: “what is the Oracle in Delphi? Tetraktys” (what is the Oracle of Delphi? Tetraktys).
There is another Tetraktys, as mentioned in Plato’s Timaeus, which is called a double Tetraktys and consists of eight lines created by the first eight numbers (1, 2, 3, 4, 5, 6, 7, which in total give a total of 36 (1+2+3+4+5+6+7+8=36). From another point of view this Quadrilateral is created, and thus connected to the regular Quadrilateral Quadrilateral, by the sum of the first four odd numbers and of the first four integers: (1+3+5+7)+(2+4+6+8)=36 as mentioned by Plutarch in “On Isis and Osiris”.
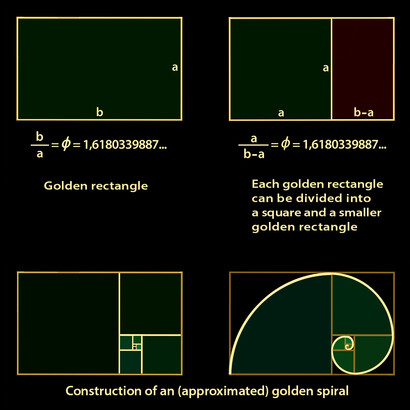
GOLDEN RATIO Φ ON THE PYTHAGORIAN SYMBOL
PARTHENON WAS BUILT on the PRNICIPLES of PYTHAGORAS
 
The FIRST FLYING MASCHINE was BUILT by the GREEK PYTHAGOEIAN PHILOSOPHER ARCHYTAS in TARANTO(CORINTHIAN COLONY) SOUTHERN ITALY.
For the Pythagoreans, a politician was the person who, after having been taught philosophy, returned to the world to be useful to others.
He is not interested in positions and powers but in the improvement of society.
The one who chose to become a politician could not pass to the stage of a mathematician, that is, one who can deliver lessons and teach.
Those who could had the advantage of living near Pythagoras.
Friendship and companionship were of the highest importance for the Pythagoreans and they considered that universal love was reflected in these two elements.
They were bound by an oath of secrecy over the higher teaching, the ceremonies and the sacred symbols.
Pythagoras offered mankind a universal “successful experiment” for this and later Plato would call education with music and gymnastics!!!!

ONE OF THE BASIC PYTHAGORIAN GROUNDS FOR: ARCHITECTURE, GEOMETRY, MUSIC, STEREOMETRY, ASTRONOMY, HARMONY AND PHILOSOPPHY

WHAT DID PYTHAGORAS SAYABOUT WOMAN=ΓΥΝΗ/GYNE
https://euphoriatric.com/pythagoras-the-nine-muses/ |
|
|
|
جواب |
رسائل 271 من 271 في الفقرة |
|
Dimensions of the Cheops-pyramid (Khufu's pyramid)
Numbers and figures of the Cheops (Khufu) pyramid:
The pyramid of Khufu - Output / performance - Building material - Dimensions of the pyramid - Dimensions in Royal Cubits - Sources
 Cheops-pyramid (pyramid of Khufu) Cheops-pyramid (pyramid of Khufu)
Of the the famous Seven Wonders of the Ancient World the Great Pyramid of Khufu (Cheops) at Giza is the only one still standing. Even for modern men it is amazing how this man-made structure lasted so long.
The Giza pyramids must have made an incredible visual impact - at the edge of the desert three abstract geometrical symbols were rising, huge luminous white triangles reflecting the blinding light of the sun!
The pyramids on the Giza plateau are with 146.59m (Khufu / Cheops) and 143.87m (Khafre / Chefren) respectively the largest, however there are over 30 major pyramids and a myriad of smaller pyramids in Egypt.
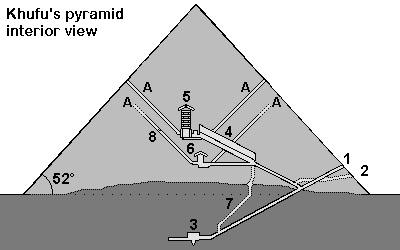
Cheops-Pyramid
1. Entrance 2. Entrance cut by grave robbers 3. Subterranean chamber 4. Grand Gallery 5. King's chamber, relieving chambers, granite portcullis slabs 6. Queen's chamber 7. Shaft 8. Limestone plugging the air shaft A= "Air shafts"
 Output / performance Output / performance
 Detailed calculations how many workers were necessary to build the pyramid Detailed calculations how many workers were necessary to build the pyramid
 Overview pyramid building Overview pyramid building
Builder
------------------- |
|
Khufu (Chuefui-Chnum or Khnum-Khuf, Cheops in Greek) during the 4th dynasty of the old kingdom |
| Time to build |
|
Probably max. 23 years (Khufu reigned from 2551 to 2528 before Christ *). Herodotus writes about 10 years of preparation and 20 years of building (details of the text) |
| Per day |
|
With 2'500'000 stones 342 stones have to be moved daily (working during 365 days a year) or 431 stones daily (working during 290 days a year). |
|
Per minute
|
|
10-hour day: every 2 minutes a stone (34 to 43 per hour)
8-hour day: nearly a stone every minute (42 to 53 stones per hour)
|
| Rule of thumb |
|
| While construction the pyramid the rate of delivery was 1 stone weighting 2.5 tons every minute. |
For our calculations we assume 500 stones a day. This is a rough estimate, assuming a 8-hour day, during 290 days a year, with 20 years to build the pyramid. Also assuming, that more time had to be used for the huge granite blocks for the King's chamber and for the more difficult upper part of the pyramid, where work went slower than in the lower parts. There probably were also other factors delaying the building of the pyramid such as the weather or a temporary shortage of certain building materials.
|
 Building materials for the Cheops-pyramid Building materials for the Cheops-pyramid
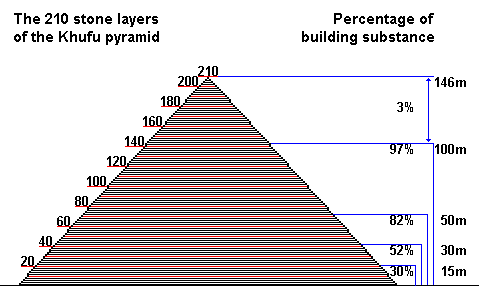
The Khufu-pyramid (Cheops) probably originally had 210 stone layers. At 50m height already 82% of the entire pyramid was built [3].
 Quarrying stones for the pyramid Quarrying stones for the pyramid
 Shipping the stone blocks down the Nile to Giza Shipping the stone blocks down the Nile to Giza
 Transporting the stone blocks using a sledge on tracks Transporting the stone blocks using a sledge on tracks
 Löhner's rope roll Löhner's rope roll
Stone blocks
------------------- |
|
2'300'000 stones |
| Casing blocks |
|
115'000 to 200'000 stones or 67'390m³ [1] |
| Total blocks |
|
2'500'000 stones |
| Stone layers |
|
Originally probably 210 stone layers, now only 201 layers [2] |
| Stone size |
|
The stone blocks usually are larger in the lower layers (1.5m = 3 cubit) and smaller in the upper layers. Most are between 1.5 and 2 cubit large (average of 127 x 127 x 71cm). 1 cubit = 0.524m - Details |
| Weight of the stone blocks |
|
With an average density of 2,6 - 2,9 t/m³ the large limestone blocks weighted 6.5 - 10 tons and the smaller ones about 1.3 tons. For all calculations on this website an average weight of 2.5 tons was used. |
| Special blocks |
|
For the King's chamber granite blocks weighting 40 to 50 tons were used |
| Total weight |
|
6'500'000 tons (average weight of a block was about 2.5 tons) |
| Pyramidion |
|
The final stone on the top was a large block in the shape of a pyramid. It was perhaps around 1.5m by 1.5m wide and 1.3m high (about 3 cubits). It was made from white Tura limestone (Turah), granite or perhaps diorite and perhaps gold plated. More information |
| Building materials |
|
Pyramid: Nummulite limestone from quarries about 200-400m south of the pyramid were used for the core stones.
Casing: light white limestone, so called Tura-limestone from quarries from the eastern shores of the Nile
King's chamber: Rose granite from Aswan 900km away
Further materials: Graywacke from the Wadi Hammamat (Eastern desert), basalt from the northern Faiyum
 Map of quarries in Egypt Map of quarries in Egypt
|
 Dimensions of the pyramid of Khufu Dimensions of the pyramid of Khufu
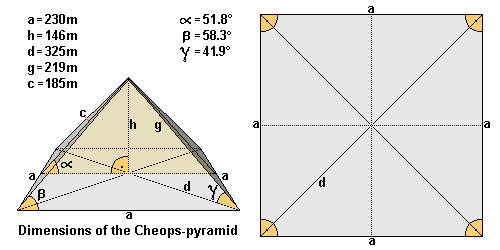
Length (a)
------------------- |
|
The average length of the edge is ~ 230.360m (230,12m = 440 cubits). Northern edge 230.328m - eastern edge 230.369m - southern edge 230.372m - western edge 230.372m. Largest difference is only 4.4cm. [3] |
| Height (h) |
|
Originally 146.59m high (= 280 cubits), the pyramid is now only 138.75m high [7] |
| Diagonal (d) |
|
325.77m |
| Ridge (g) |
|
219m |
| Height of the lateral surface |
|
186.42m |
| Pyramid angle α |
|
51° 50' 40' = inclination of the lateral surface (= 52° rounded off) [3] which corresponds to a seked of 5½ palms |
| Pyramid angle β |
|
58.3° = the two angles of the triangular lateral surface (62° = angle of the apex or tip of the pyramid) - nearly forming an equilateral triangle! |
| Pyramid angle γ |
|
41.9° = angle of the ridge |
| Corner angle |
|
Right angle base with angles from 89° 59' to 90° |
| Base area |
|
53'065.73m² |
| Superficies surface |
|
85'890.69m² |
| Pyramid volume |
|
2'592'968.43m³ including the rock core. This would be a cube with a length of 137.38m. Probable volume of stones used: 2'583'283m³ [1] or 2'326'501m³ [2]. |
| Alignment |
|
Exactly to the north (deviation only 2' 28') |
| Latitude and longitude |
|
N 29° 58’ 44.3830” latitude and E 31° 07’ 57.0194” longitude [5] |
| Altitude |
|
The base of the pyramid of Khufu lies about 60m above sea level, so the tip of the pyramid used to be on 206m above sea level [6]. |
 Alignment of the pyramids and controlling the shape of the pyramid (north-south alignment etc.) Alignment of the pyramids and controlling the shape of the pyramid (north-south alignment etc.)
 Dimensions of the pyramid of Khufu in Egyptian Royal Cubits Dimensions of the pyramid of Khufu in Egyptian Royal Cubits
 |
Length (a) |
|
440 Royal Cubits |
| Height (h) |
|
280 Royal Cubits |
| Height of the lateral surface (c) |
|
356 Royal Cubits (356.09) |
| Diagonal (d) |
|
622.25 Royal Cubits |
| Ridge (g) |
|
418.56 Royal Cubits |
| Pyramid angle α |
|
51.843° |
| Pyramid angle β |
|
58.3° |
| Pyramid angle γ |
|
41.9° |
| Corner angle |
|
90° |
It is suggested, that the Egyptians used a right angled triangle to determinate the angle of inclination of the pyramid, using the numbers a=11 and b=14 with c=17.8 (or a=22 - b=28 - c= 35.6). This determines a so called seked of 5½ palms.
 Alignment of the pyramids and controlling the shape of the pyramid (seked) Alignment of the pyramids and controlling the shape of the pyramid (seked)
 Sources Sources
[1] M. Lehner The Complete Pyramids of Egypt
[2] G. Goyon Die Cheops-Pyramide
[3] R. Stadelmann Die grossen Pyramiden von Giza
[4] F. Abitz Der Bau der grossen Pyramide mit einem Schrägaufzug
[5] GPS-coordinates of a brass disk on top of the pyramid of Khufu, Giza Plateau Mapping Project (GPMP)
[6] Maps of the Giza Plateau Mapping Project show the altitude as 60m
[7] D. Arnold Building in Egypt
* Dates according to conventional Egyptian chronology are used in this website. These are based on several list of the dynasties of pharaohs, for example the Aegyptiaca of Manetho of Sebennytos.
https://www.cheops-pyramide.ch/khufu-pyramid/khufu-numbers.html |
|
|
 أول أول
 سابق
257 a 271 de 271
لاحق سابق
257 a 271 de 271
لاحق
 آخر
آخر
|