|
Rispondi |
Messaggio 1 di 79 di questo argomento |
|
 In ‘Les Archives de Rennes-le-Chteau’, published in 1988, Pierre Jarnac wrote: "His – Louis Lawrence’s – grandmother, Marie Rivarès, died on 28 November 1922, the year after moving to Les Pontils. In accordance with the wishes of the deceased, the body was…embalmed! It was there in the tomb [sépulture = burial place] prepared originally by the Galibert family that Louis Lawrence buried the body. Some time later, in 1931 or 1932, he did the same thing upon the death of his mother, Emily Rivarès, whom he laid to rest in the tomb [tombeau = tomb] with the remains of two cats, also mummified!It was then that there was erected, on this site, a tomb [tombeau = tomb] in parallelepiped form, surmounted by a truncated pyramid. The whole structure was covered by a screed of cement. Nothing therefore served to distinguish it from those numerous funerary monuments that, at this time, one could still see in large numbers along the roadside." So the tomb that once existed in Les Pontils was only built in 1933 by Louis Lawrence to contain the dead bodies of his mother, grandmother, and two mummified cats. Previously it had been a grave containing the corpses of the Galibert family. Pierre Jarnac obtained his information from Adrien Bourrel, the second son of Louis Lawrence. And the stonemason Bourrel who dug the first grave in 1903 was related to the common-law wife of Louis Lawrence. Quoting Pierre Jarnac from private correspondence: "As for the year 1903 it was not the 'tomb' strictly speaking that was constructed in that year but only the 'basic' tombstone [dalle funéraire] covering a grave. The actual tomb - in other words the parallelepiped that bore so much resemblance to the tomb of Poussin - was only built around 1933".   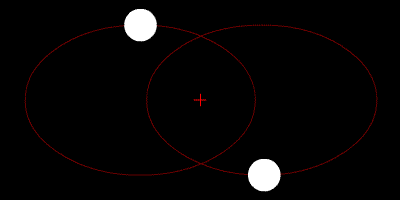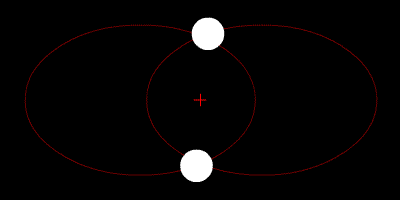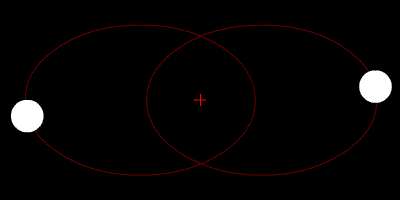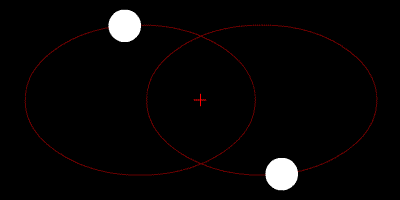 The term Kilkenny cat refers to anyone who is a tenacious fighter. The origin of the term is now lost so there are many stories purporting to give the true meaning. To "fight like a Kilkenny cat" refers to an old story about two cats who fought to the death and ate each other up such that only their tails were left. There is also a limerick (with optional added couplet) about the two cats: There once were two cats of Kilkenny Each thought there was one cat too many So they fought and they fit And they scratched and they bit 'Til (excepting their nails And the tips of their tails) Instead of two cats there weren't any!Kil - k = 11 enny - any Interpretations of Schroedinger's Cat
Stephen Hawking is famously quoted as saying "When I hear about Schroedinger's cat, I reach for my gun."
_________________
E.T.A.E
|
|
|
|
Rispondi |
Messaggio 2 di 79 di questo argomento |
|
Schrödinger Cat eye nebula Ammonia avenue Draconian suicide Alan Parsons project - La Sagrada Familia - Eye in the sky Gaudi Finca Guell Hesperides dragon Barcelona - Cat-a-lonia 4 Cats restaurant The paradox has been the subject of much controversy both scientifically and philosophically, to the point that Stephen Hawking has said, "every time I hear about that cat, I begin to get my gun", referring to the quantum suicide, a variant of the experiment of Schrödinger. http://en.wikipedia.org/wiki/Schr%C3%B6dinger%27s_catSchrödinger's cat is a thought experiment, sometimes described as a paradox, devised by Austrian physicist Erwin Schrödinger in 1935. It illustrates what he saw as the problem of the Copenhagen interpretation of quantum mechanics applied to everyday objects. The scenario presents a cat that might be alive or dead, depending on an earlier random event. Although the original "experiment" was imaginary, similar principles have been researched and used in practical applications. The thought experiment is also often featured in theoretical discussions of the interpretation of quantum mechanics. In the course of developing this experiment, Schrödinger coined the term Verschränkung (entanglement). Origin and motivation Schrödinger intended his thought experiment as a discussion of the EPR article—named after its authors Einstein, Podolsky, and Rosen—in 1935.[1] The EPR article highlighted the strange nature of quantum entanglement, which is a characteristic of a quantum state that is a combination of the states of two systems (for example, two subatomic particles), that once interacted but were then separated and are not each in a definite state. The Copenhagen interpretation implies that the state of the two systems undergoes collapse into a definite state when one of the systems is measured. Schrödinger and Einstein exchanged letters about Einstein's EPR article, in the course of which Einstein pointed out that the state of an unstable keg of gunpowder will, after a while, contain a superposition of both exploded and unexploded states. To further illustrate the putative incompleteness of quantum mechanics, Schrödinger describes how one could, in principle, transpose the superposition of an atom to large-scale systems. He proposed a scenario with a cat in a sealed box, wherein the cat's life or death depended on the state of a subatomic particle. According to Schrödinger, the Copenhagen interpretation implies that the cat remains both alive and dead (to the universe outside the box) until the box is opened. Schrödinger did not wish to promote the idea of dead-and-alive cats as a serious possibility; quite the reverse, the paradox is a classic reductio ad absurdum.[2] The thought experiment illustrates the counterintuitiveness of quantum mechanics and the mathematics necessary to describe quantum states. Intended as a critique of just the Copenhagen interpretation (the prevailing orthodoxy in 1935), the Schrödinger cat thought experiment remains a typical touchstone for all interpretations of quantum mechanics. Physicists often use the way each interpretation deals with Schrödinger's cat as a way of illustrating and comparing the particular features, strengths, and weaknesses of each interpretation. [edit]The thought experiment Schrödinger wrote:[3][2] One can even set up quite ridiculous cases. A cat is penned up in a steel chamber, along with the following device (which must be secured against direct interference by the cat): in a Geiger counter, there is a tiny bit of radioactive substance, so small that perhaps in the course of the hour, one of the atoms decays, but also, with equal probability, perhaps none; if it happens, the counter tube discharges, and through a relay releases a hammer that shatters a small flask of hydrocyanic acid. If one has left this entire system to itself for an hour, one would say that the cat still lives if meanwhile no atom has decayed. The psi-function of the entire system would express this by having in it the living and dead cat (pardon the expression) mixed or smeared out in equal parts. It is typical of these cases that an indeterminacy originally restricted to the atomic domain becomes transformed into macroscopic indeterminacy, which can then be resolved by direct observation. That prevents us from so naively accepting as valid a "blurred model" for representing reality. In itself, it would not embody anything unclear or contradictory. There is a difference between a shaky or out-of-focus photograph and a snapshot of clouds and fog banks. —Erwin Schrödinger, Die gegenwärtige Situation in der Quantenmechanik (The present situation in quantum mechanics), Naturwissenschaften (translated by John D. Trimmer in Proceedings of the American Philosophical Society) Schrödinger's famous thought experiment poses the question, when does a quantum system stop existing as a superposition of states and become one or the other? (More technically, when does the actual quantum state stop being a linear combination of states, each of which resembles different classical states, and instead begins to have a unique classical description?) If the cat survives, it remembers only being alive. But explanations of the EPR experiments that are consistent with standard microscopic quantum mechanics require that macroscopic objects, such as cats and notebooks, do not always have unique classical descriptions. The thought experiment illustrates this apparent paradox. Our intuition says that no observer can be in a mixture of states—yet the cat, it seems from the thought experiment, can be such a mixture. Is the cat required to be an observer, or does its existence in a single well-defined classical state require another external observer? Each alternative seemed absurd to Albert Einstein, who was impressed by the ability of the thought experiment to highlight these issues. In a letter to Schrödinger dated 1950, he wrote: You are the only contemporary physicist, besides Laue, who sees that one cannot get around the assumption of reality, if only one is honest. Most of them simply do not see what sort of risky game they are playing with reality—reality as something independent of what is experimentally established. Their interpretation is, however, refuted most elegantly by your system of radioactive atom + amplifier + charge of gunpowder + cat in a box, in which the psi-function of the system contains both the cat alive and blown to bits. Nobody really doubts that the presence or absence of the cat is something independent of the act of observation.[4] Note that no charge of gunpowder is mentioned in Schrödinger's setup, which uses a Geiger counter as an amplifier and hydrocyanic poison instead of gunpowder. The gunpowder had been mentioned in Einstein's original suggestion to Schrödinger 15 years before, and apparently Einstein had carried it forward to the present discussion.
Kaon - Koan...
_________________
'Conceal me what I am, and be my aid, for such disguise as haply shall become, the form of my intent'.
|
|
|
|
Rispondi |
Messaggio 3 di 79 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 4 di 79 di questo argomento |
|
Universos paralelos
De Wikipedia, la enciclopedia libre
Universos paralelos es el nombre de una hipótesis física, en la que entran en juego la existencia de varios universos o realidades relativamente independientes. El desarrollo de la física cuántica, y la búsqueda de una teoría unificada (teoría cuántica de la gravedad), conjuntamente con el desarrollo de la teoría de cuerdas, han hecho entrever la posibilidad de la existencia de múltiples dimensiones y universos paralelos conformando un multiverso.
Universos paralelos o términos similares también se encuentran como temáticas de la literatura, particularmente en lo que por ejemplo se refiere al género literario fantastique.
Universos paralelos en física[editar]
Teoría de los universos[editar]

La paradoja cuántica del «gato de Schrödinger» vista desde el punto de vista de la interpretación de los universos múltiples.En esta interpretación cada evento involucra un punto de ramificación en el tiempo, el gato está vivo y muerto, incluso antes de que la caja se abra, pero los gatos «vivos» y «muertos» están en diferentes ramificaciones del universo, por lo que ambos son igualmente reales, pero no pueden interactuar el uno con el otro.[1]
Una de las versiones científicas más curiosas que recurren a los universos paralelos es la interpretación de los universos múltiples o interpretación de los mundos múltiples (IMM), de Hugh Everett.[2] Dicha teoría aparece dentro de la mecánica cuántica como una posible solución al problema de la medida en mecánica cuántica. Everett describió su interpretación más bien como una metateoría. Desde un punto de vista lógico la construcción de Everett evade muchos de los problemas asociados a otras interpretaciones más convencionales de la mecánica cuántica. Recientemente sin embargo, se ha propuesto que universos adyacentes al nuestro podrían dejar una huella observable en la radiación de fondo de microondas, lo cual abriría la posibilidad de probar experimentalmente esta teoría.[3] El problema de la medida es uno de los principales «frentes filosóficos» que abre la mecánica cuántica. Si bien la mecánica cuántica ha sido la teoría física más precisa hasta el momento, permitiendo hacer cálculos teóricos relacionados con procesos naturales que dan 20 decimales correctos y ha proporcionado una gran cantidad de aplicaciones prácticas (centrales nucleares, relojes de altísima precisión, ordenadores), existen ciertos puntos difíciles en la interpretación de algunos de sus resultados y fundamentos (el premio Nobel Richard Feynman llegó a bromear diciendo «creo que nadie entiende verdaderamente la mecánica cuántica»).
El problema de la medida se puede describir informalmente del siguiente modo:
- De acuerdo con la mecánica cuántica un sistema físico, por ejemplo un conjunto de electrones orbitando en un átomo, queda descrito por una función de onda. Dicha función de onda es un objeto matemático que supuestamente describe la máxima información posible que contiene un estado puro.
- Si nadie externo al sistema ni dentro de él observara o tratara de ver como está el sistema, la mecánica cuántica nos diría que el estado del sistema evoluciona determinísticamente. Es decir, se podría predecir perfectamente hacia dónde irá el sistema.
- La función de onda nos informa cuáles son los resultados posibles de una medida y sus probabilidades relativas, pero no nos dice qué resultado concreto se obtendrá cuando un observador trate efectivamente de medir el sistema o averiguar algo sobre él. De hecho, la medida sobre un sistema es un valor aleatorio entre los posibles resultados.
Eso plantea un problema serio: si las personas y los científicos u observadores son también objetos físicos como cualquier otro, debería haber alguna forma determinista de predecir cómo tras juntar el sistema en estudio con el aparato de medida, finalmente llegamos a un resultado determinista. Pero el postulado de que una medición destruye la «coherencia» de un estado inobservado e inevitablemente tras la medida se queda en un estado mezcla aleatorio, parece que sólo nos deja tres salidas:[4]
- (A) O bien renunciamos a entender el proceso de decoherencia, por lo cual un sistema pasa de tener un estado puro que evoluciona deterministicamente a tener un estado mezcla o «incoherente».
- (B) O bien admitimos que existen unos objetos no-físicos llamados «conciencia» que no están sujetos a las leyes de la mecánica cuántica y que nos resuelven el problema.
- (C) O tratamos de proponer una teoría que explique el proceso de medición, y no sean así las mediciones quienes determinen la teoría.
Diferentes físicos han tomado diferentes soluciones a este «trilema»:
- Niels Bohr, que propuso un modelo inicial de átomo que acabó dando lugar a la mecánica cuántica y fue considerado durante mucho tiempo uno de los defensores de la interpretación ortodoxa de Copenhague, se inclinaría por (A).
- John von Neumann, el matemático que creó el formalismo matemático de la mecánica cuántica y que aportó grandes ideas a la teoría cuántica, se inclinaba por (B).
- La interpretación de Hugh Everett es uno de los planteamientos que apuesta de tipo (C).
La propuesta de Everett es que cada medida «desdobla» nuestro universo en una serie de posibilidades (o tal vez existían ya los universos paralelos mutuamente inobservables y en cada uno de ellos se da una realización diferente de los posibles resultados de la medida). La idea y el formalismo de Everett es perfectamente lógico y coherente, aunque algunos puntos sobre cómo interpretar ciertos aspectos, en particular cómo se logra la inobservabilidad o coordinación entre sí de esos universos para que en cada uno suceda algo ligeramente diferente. Pero por lo demás es una explicación lógicamente coherente y posible, que inicialmente no despertó mucho entusiasmo sencillamente porque no está claro que sea una posibilidad falsable.
El Principio de simultaneidad dimensional, establece que: dos o más objetos físicos, realidades, percepciones y objetos no-físicos, pueden coexistir en el mismo espacio-tiempo. Este principio tiene correspondencia biunívoca con la teoría de Interpretación de Mundos Múltiples, IMM y la teoría de Multiverso de nivel III, aunque no ha sido planteado por Hugh Everett, ni tampoco por Max Tegmark.
Sin embargo, en una encuesta sobre la IMM, llevada a cabo por el investigador de ciencias políticas L. David Raub, que entrevistó a setenta y dos destacados especialistas en cosmología y teóricos cuánticos, dio los siguientes resultados:
| Resultados de la encuesta sobre la IMM[5] |
| Respuesta | Sí, creo que la IMM
es correcta | No acepto la IMM | Quizás la IMM sea correcta,
pero aún no estoy convencido | No tengo una opinión ni a favor
ni en contra |
| Resultados |
58% |
18% |
13% |
11% |
Entre los especialistas que se inclinaron por (1) estaban, Stephen Hawking, Richard Feynman o Murray Gell-Mann, entre los que se decantaron por (2) estaba Roger Penrose. Aunque Hawking y Gell-Mann han explicado su posición. Hawking afirma en una carta a Raub que «El nombre 'Mundos Múltiples' es inadecuado, pero la teoría, en esencia, es correcta» (tanto Hawking como Gell-Mann llaman a la IMM, 'Interpretación de Historias Múltiples'). Posteriormente Hawking ha llegado a decir que «La IMM es trivialmente verdadera» en cierto sentido. Por otro lado Gell-Man en una reseña de un artículo del físico norteamericano Bruce DeWitt, uno de los principales defensores de la IMM, Murray Gell-Mann se mostró básicamente de acuerdo con Hawking: «... aparte del empleo desacertado del lenguaje, los desarrollos físicos de Everett son correctos, aunque algo incompletos». Otros físicos destacados como Steven Weinberg o John A. Wheeler se inclinan por la corrección de esta interpretación. Sin embargo, el apoyo de importantes físicos a la IMM refleja sólo la dirección que está tomando la investigación y las perspectivas actuales, pero en sí mismo no constituye ningún argumento científico adicional en favor de la teoría.
Los agujeros negros como entrada a los universos paralelos[editar]
Se ha apuntado que algunas soluciones exactas de las ecuación del campo de Einstein pueden extenderse por continuación analítica más allá de las singularidades dando lugar a universos espejos del nuestro. Así la solución de Schwarzschild para un universo con simetría esférica en el que la estrella central ha colapsado comprimiéndose por debajo de su radio de Schwarzschild podría ser continuada analíticamente a una solución de agujero blanco (un agujero blanco de Schwarzchild se comporta como la reversión temporal de un agujero negro de Schwarzschild).[6] La solución completa describe dos universos asintóticamente planos unidos por una zona de agujero negro (interior del horizonte de sucesos). Dos viajeros de dos universos espejos podrían encontrarse, pero sólo en el interior del horizonte de sucesos, por lo que nunca podrían salir de allí.
Una posibilidad igualmente interesante son los universos Reissner-Nordström y de Kerr-Newman. Este último universo es una solución posible de las ecuaciones de Einstein que puede ser continuada analíticamente a través de una singularidad espacial evitable por un viajero. A diferencia de la solución completa de Schwarzchild, la solución de este problema da como posibilidad la comunicación de los dos universos sin tener que pasar por los correspondientes horizontes de sucesos través de una zona llamada horizonte interno.
Los universos paralelos en la ficción[editar]
La temática de los universos paralelos y de otras dimensiones es muy frecuente en la ficción. Si bien es la ciencia ficción la que más se ha destacado, también se utiliza en el género del terror (H. P. Lovecraft, Brian Lumley, por ejemplo), en la fantasía (C. S. Lewis, por ejemplo) e incluso en el drama histórico (Harry Turtledove, Vladimir Nabokov, entre otros).
En algunos casos un universo paralelo es similar al nuestro pero con eventos históricos diferentes, aunque en otros (frecuentemente en historias de horror) otro universo ó dimensión son lugares sombríos e infernales repletos de formas de vida monstruosas (ejemplos Event Horizon, Doom, etc.).Actualmente un chico investigador, fisico llamado Cesar Alexander Calvay hizo la ecuacion del multi universo dimencional MUD=( t/ep+ef )oo.
MUD= Multi Universo Dimensional t= tiempo ep: espacio pasado, ef= espacio futuro, oo= elevado al exponente infinito.
Véase también[editar]
|
|
|
 Primo
Primo
 Precedente
2 a 4 de 79
Successivo
Precedente
2 a 4 de 79
Successivo Ultimo
Ultimo
|

