|
Rispondi |
Messaggio 1 di 455 di questo argomento |
|
-
saintseiyaforos.net/.../71127-según-ustedes-en-que-categoría-podemos-ubicar -a-saturno/
Editado por Iccc, 20 abril 2014 - 06:28 . ... como dijeron varios, saturno es el
equivalente romano de cronos, el titan que engendro a los ...
-
saintseiyaforos.net/topic/70769-¿el-dios-cronos-kronos.../page-2
Editado por zeus god king, 20 abril 2014 - 13:13 . .... crono y saturno son el
simbolo del tiempo que es otra cosa ..por que ambos son los ...
-
entremujeres.clarin.com/.../saturno-astros-astrologia-trabajo-profesion- vocacion-beatriz-leveratto-columnista_0_982101865.html
Es la ley de lo irrefutable, la ley de gravedad, “Cronos”: el paso del tiempo.
Muestra la ... Excepto el período del de 15 octubre de 2000 al 20 de abril de
2001.
-
noticiasdiarias.com.ve/2015/.../saturno-cronos-el-senor-del-tiempo/
5 Ene 2015 ... Saturno – Cronos, el señor del tiempo. ... Compartir Aries del 21 de Marzo al 20
de Abril Recibes propuestas interesantes en apariencia, pero ...
-
norfipc.com/.../simbolos-signos-unicode-planetas-astronomia-horoscopo.php
Toma su nombre de Urano, padre de Crono (Saturno) en la mitología griega. ...
Es la constelacion que rige los nacidos desde el 21 de marzo al 20 de abril.
-
liberatuser.es/terapiasalternativaslossignosastrologicos.html
Rige a las personas nacidas entre el 21 de Marzo y el 20 de Abril. ..... En la
antigua Mitología Romana, Saturno (y su equivalente griego, Cronos) es el
padre de ...
-
www.upv.es/satelite/trabajos/pracGrupo1/saturno/crono.htm
El siguiente es un resumen de los Anillos de Saturno: ... W. Herschel 1789 Tetis
III 530 7.55e+20 294,660 G. Cassini 1684 Telesto XIII 17x14x13 ? ... Pioneer 11 -
USA Júpiter/Saturno - 259 kg - (Abril 6, 1973 - Noviembre 1995) Pioneer 11 ...
-
https://astrofanaticos.wordpress.com/2012/04/13/
13 Abr 2012 ... de circulosolar en Uncategorized Etiquetas:saturno, sistema solar. Saturno o
Cronos(su nombre para los griegos) se le considera el dios de las cosechas y el
tiempo. Sus padres ... 16, 17, 18, 19, 20, 21, 22. 23, 24, 25, 26, 27 ...
-
elmundodesaramujerde35.blogspot.com/.../saturno-o-cronos-relatos- mitologicos.html
14 Dic 2010 ... Pero, me gusto la historia del Dios Saturno y hoy quiero compartirla con ustedes.
... cuando se casa Cronos o Saturno, tuvo muchos hijos y le exigía a su mujer
que le entregara los recién nacidos ... Anónimo 18 de diciembre de 2010, 8:20 ....
julio (30). ▻ junio (25). ▻ mayo (27). ▻ abril (29). ▻ marzo (20) ...
-
astrojem.com/teorias/titan.html
Con él, tuvo la inmensa alegría de ver los cuatro satélites de Saturno
descubiertos por Galileo. ... y hermanas de Crono (el nombre griego para el dios
romano del tiempo Saturno) para .... Noticia del 20 de abril de 2012, publicada
por la ESA.
|
|
|
|
Rispondi |
Messaggio 261 di 455 di questo argomento |
|
| Reply |
Message 337 of 350 on the subject |
|
|
|
|
| Reply |
Message 338 of 350 on the subject |
|
|
6. Apocalipsis 3:7: Escribe al ángel de la iglesia en Filadelfia: Esto dice el Santo, el Verdadero, el que tiene la LLAVE de David, el que abre y ninguno cierra, y cierra y ninguno abre:
|
|
|
| Reply |
Message 339 of 350 on the subject |
|
|
|
|
| Reply |
Message 340 of 350 on the subject |
|
|
|
|
|
|
|
Rispondi |
Messaggio 262 di 455 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 263 di 455 di questo argomento |
|
Perséfone
De Wikipedia, la enciclopedia libre
En la mitología griega, Perséfone (en griego antiguo, Περσεφόνη Persephónē: ‘la que lleva la muerte’) es hija de Zeus y de Deméter (ἡ Μητὴρ hē Mētḕr: ‘la madre’). La joven doncella, llamada hasta entonces Kore (Κόρη: ‘hija’), es raptada por Hades y se convierte en la reina del Inframundo.
Perséfone es su nombre en la literatura épica de la Grecia jónica.[1] En otros dialectos era conocida por otros nombres, como Persephassa o Persephatta. Homero la llama Persephoneia (Περσεφόνεια). Los romanos tuvieron noticia de ella por primera vez a través de las ciudades eólicas y dóricas de la Magna Grecia, donde usaban la variante dialéctica Proserpina.
De ahí que en la mitología romana fuese llamada Proserpina, y como tal llegase a convertirse en un personaje emblemático del Renacimiento.
Visión general[editar]
La figura de Perséfone es actualmente muy conocida. Su historia tiene un gran poder emocional: una doncella inocente, el dolor de una madre por el rapto y el regreso de su hija. También es citada con frecuencia como un paradigma de los mitos que explican procesos naturales, con el descenso y el regreso de la diosa provocando el cambio de estación.
Pero los griegos también conocían otra faceta de Perséfone. Ella era además la terrible Reina de los muertos, cuyo nombre no era seguro pronunciar en voz alta y a la que se referían como «La Doncella». En la Odisea, cuando Odiseo viaja al Inframundo, alude a ella como «Reina de Hierro». Su mito central, aún con toda su familiaridad emotiva, era también el contexto tácito de los extraños ritos iniciáticos secretos de regeneración de los misterios eleusinos, que prometían la inmortalidad a sobrecogidos participantes: una inmortalidad en el mundo subterráneo de Perséfone, en un banquete con los héroes bajo su pavorosa mirada.[2]
El mito del rapto[editar]

Grabado de 1690, obra de Johann Ulrich Krauß (1655-1719): Las compañeras de Perséfone son transformadas en sirenas.
En el panteón olímpico se le da un padre a Perséfone: según la Teogonía de Hesíodo era hija de Zeus y Deméter:
Y él [Zeus] fue a la cama de la abundante Démeter, quien concibió a Perséfone, la de blancos brazos, robada por Hades del lado de su madre.
Sin embargo, Deméter no tenía una posición estable en el Olimpo. Solía vivir muy lejos de los demás dioses, siendo una diosa de la naturaleza anterior a plantar semillas y cultivar plantas. En la tradición olímpica fue cortejada por los dioses Hermes, Ares, Apolo y Hefesto, pero ella rechazó todos sus regalos y alejó a su hija de la compañía de los dioses. Así, llevaba una vida pacífica hasta que su hija Perséfone se convirtió en la reina del inframundo, lo que, según los mitógrafos olímpicos, no sucedió hasta que Hades la raptó y la llevó allí con él. Perséfone estaba cogiendo flores inocentemente con algunas ninfas (y Atenea y Artemisa, según el himno homérico, o Leucipe, o algunas Oceánides) en un campo en Enna cuando Hades apareció, emergiendo de una grieta del suelo. Las ninfas fueron castigadas siendo transformadas en las Sirenas por no haber intervenido. La vida quedó paralizada mientras la desolada Deméter buscaba por todas partes a su hija perdida. Hécate había oído sus gritos y sugirió a Démeter hablar con Helios, el sol, que todo lo ve, para que le contase lo que había pasado.
Finalmente, Zeus no pudo aguantar más la agonía de la tierra y obligó a Hades a devolver a Perséfone, enviando a Hermes para rescatarla. La única condición que se puso para liberar a Perséfone fue que no probase bocado en todo el trayecto, pero Hades la engañó para que comiese seis ,o cuatro según las fuentes, semillas de granada, que la obligaban a volver cada año un mes por cada semilla. En algunas versiones, Ascálafo contaba a los demás dioses que Perséfone se había comido voluntariamente las semillas de granada. Cuando Deméter y su hija estaban juntas, la tierra florecía de vegetación. Pero durante seis meses al año, cuando Perséfone volvía a los infiernos, la tierra se convertía de nuevo en un erial estéril. Fue durante su viaje para rescatar a Perséfone del inframundo cuando Deméter reveló los misterios eleusinos. En una versión alternativa, Hécate rescató a Perséfone. En la versión más antigua la temible diosa Perséfone era la propia Reina del Inframundo.[3]
En algunas versiones Deméter prohíbe a la tierra dar frutos, en otras está tan ocupada buscando a Perséfone que no se ocupa de ella, y en algunas la profundidad de su desesperación hace que nada crezca.
El número de semillas comido por Perséfone cambia también de unas versiones a otras, a menudo en relación con la duración del invierno en la zona de procedencia de la historia.
Este mito puede ser interpretado también como una alegoría de los rituales matrimoniales de los antiguos griegos, que sentían que el matrimonio era una especie de rapto de la novia de su familia por parte del novio, y este mito puede haber explicado los orígenes del ritual del matrimonio. La más popular explicación etiológica de las estaciones puede haber sido una interpretación posterior.
Perséfone, como reina del Hades, sólo mostró clemencia una vez. Debido a que la música de Orfeo era tan arrebatadoramente triste, permitió que éste se llevase a su esposa, Eurídice, de vuelta al mundo de los vivos con la condición de que ella caminase tras él y él nunca intentase mirarla a la cara hasta que estuviesen en la superficie. Orfeo accedió pero falló, al mirar atrás casi al final para asegurarse de que su esposa le seguía, y perdió a Eurídice para siempre.
Perséfone también figura en la historia de Adonis, el consorte sirio de Afrodita. Cuando Adonis nació, Afrodita lo tomó bajo su protección y fue hechizada por su belleza sobrenatural. Afrodita se lo dio a Perséfone para que lo cuidara, pero ésta también quedó asombrada por su belleza y rehusó devolvérselo. La discusión entre las dos diosas fue resuelta por Zeus o Calíope, quien decidió que Adonis pasase cuatro meses con Afrodita, cuatro con Perséfone y los cuatro restantes del año solo.
También departió con Psique cuando esta bajó al inframundo a buscar un cofrecito que Afrodita la había mandado a buscar.
Cuando Hades persiguió a una ninfa llamada Mente, Perséfone la convirtió en una planta de menta.
Perséfone era el objeto del cariño de Pirítoo. Su amigo Teseo y él prometieron casarse con sendas hijas de Zeus. Teseo escogió a Helena, la secuestró con la ayuda de Pirítoo y decidió retenerla hasta que tuviese la edad de casarse. Dejaron a Helena con la madre de Teseo, Etra, y viajaron al inframundo, reino de la elegida de Pirítoo, Perséfone, y del marido de ésta, Hades, quien fingió ofrecerles hospitalidad y preparó un banquete. Tan pronto como la pareja se sentó, las serpientes se enroscaron en torno a sus pies, atrapándolos. Teseo fue finalmente rescatado por Heracles.
El matrimonio formado por Perséfone y Hades fue estéril; no así ella, que fue seducida por su propio padre en forma de serpiente y tuvo un hijo: Zagreo, que fue asesinado por los Titanes a instancias de Hera.
Era frecuente referirse a Perséfone y su madre Deméter como aspectos de la misma diosa, y eran llamadas «las Deméters» o simplemente «las diosas». La historia del rapto de Perséfone era parte de los ritos de iniciación en los misterios eleusinos.
El rapto según la Enciclopedia Británica[editar]
La versión del mito que aparece en la edición de 1911 de la Enciclopedia Británica es la siguiente:
Mientras estaba recogiendo flores con sus compañeras en un prado, la tierra se abrió y Hádes, dios de los muertos, apareció y se la llevó para que fuese su reina en el inframundo. [...] Antorcha en mano, su afligida madre la buscó por todo el mundo, y al no encontrarla prohibió a la tierra seguir creciendo. Así todo aquel año no creció una sola brizna de hierba, y los hombres habrían muerto de hambre si Zeus no hubiese persuadido a Plutón de que dejase marchar a Proserpina. Pero antes de permitirle marchar Plutón le hizo comer la semilla de una granada, y que así no pudiese permanecer alejada para siempre. Por esto fue acordado que pasaría dos tercios (según autores posteriores, un tercio) de cada año con su madre y los dioses del cielo, y el resto del año con Plutón bajo la tierra. [...] Como esposa de Plutón mandaba a espectro, gobernaba a los fantasmas y llevaba a cabo las maldiciones de los hombres.
Cuando Perséfone vuelve con su marido al infierno es cuando las hojas se caen y cuando no da frutos es cuando Démeter se desespera, el otoño, y cuando Perséfone vuelve a la tierra en Primavera es cuando las flores florecen y la tierra se vuelve fértil de nuevo, dado a la alegría de su madre, Démeter.
Investigaciones modernas sobre Perséfone[editar]
¿Perséfone anterior a Grecia?[editar]
Muchos investigadores modernos han argumentado que el culto a Perséfone fue una continuación de la adoración que ya se le profesaba en el Neolítico o en la civilización minoica. Entre los clasicistas, esta tesis ha sido defendida por Günter Zuntz[4] y cautamente incluida por Walter Burkert en su definitivo libro La religión griega.
Con mayor atrevimiento, el mitólogo Károly Kerényi ha identificado a Perséfone con la anónima «señora del laberinto» de Cnosos.
Por otra parte, la hipótesis de un culto universal a la Madre Tierra ha estado bajo creciente crítica en los últimos años. Para saber más sobre esta controversia, vea el artículo Diosa Madre.
Vida, muerte y resurrección[editar]
Inspirados por James Frazer, Jane Ellen Harrison y los mitólogos modernos, algunos investigadores han etiquetado a Perséfone como una deidad de vida, muerte y resurrección.
Consortes y descendencia[editar]
Véase también[editar]
https://es.wikipedia.org/wiki/Pers%C3%A9fone |
|
|
|
Rispondi |
Messaggio 264 di 455 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 265 di 455 di questo argomento |
|
LA INDEPENDENCIA DE ESTADOS UNIDOS CODIFICADA EN LAS 24 HORAS QUE TIENE UN DIA
EFECTIVAMENTE TENEMOS QUE EN 74 DIAS (INDEPENDENCIA DE EEUU FUE UN 4/7 O 7/4) TENEMOS EXACTAMENTE 1776 HORAS (AÑO 1776)
 |
|
24 * 74 = 1776
|
LAS MATEMATICAS SON EXACTAS PARA EL TODOPODEROSO
HECHOS 12:12 (12+12=24 HORAS)
JUAN MARCOS= SANTO GRIAL
EL DIA NUMERO 74 DEL CALENDARIO LUNI-SOLAR HEBREO ES EL 15 DE SIVAN O 15/3 (VESICA PISCIS="OJO DE GATO")
ULTRA SECRETO DEL PORQUE GEORGE MC FLY MUERE EN UN 15/3 EN LA PELICULA "VOLVER AL FUTURO II". ES OBVIA LA REFERENCIA AL "EXPERIMENTO FILADELFIA", EN EL MARCO A LA CREACION DIVINA.
EN 36 DIAS TENEMOS
 |
|
24 * 36 = 864
|
OBVIO NEXO CON SIRIO / JERUSALEN
EN 33 DIAS
 |
|
24 * 33 = 792
|
OBVIO NEXO CON LOS 7920, QUE ES EL DIAMETRO DE LA TIERRA EN MILLAS INGLESAS, EN EL MARCO AL DISEÑO DE LA GRAN PIRAMIDE.
|
|
|
|
Rispondi |
Messaggio 266 di 455 di questo argomento |
|
 15-01-2010, 06:01 PM 15-01-2010, 06:01 PM |
#146 |
|
Senior Member
Join Date: Nov 2009
Location: Mid-Atlantic
Posts: 1,419
Likes: 0 (0 Posts)
|
 Black Sun Black Sun
|
|
|
|
|
Rispondi |
Messaggio 267 di 455 di questo argomento |
|
  United Nations Security Council Chambers....  Can these folks fook with your DNA? EH? all coincidences? Quote:
The United Nations and the Freemasonry (Die Freimauerei) have both a common chamber in their palaces, either called chambers of reflection, or room for silent reflection, as at the UN headquarters.

Masonic Chamber of ReflectionsWOW I knew that image looked familiar. Real familiar ... beyond the 'skull' and the St. John the Baptist connections. Anybody else recognize it? This gets interesting and is a path to respect... 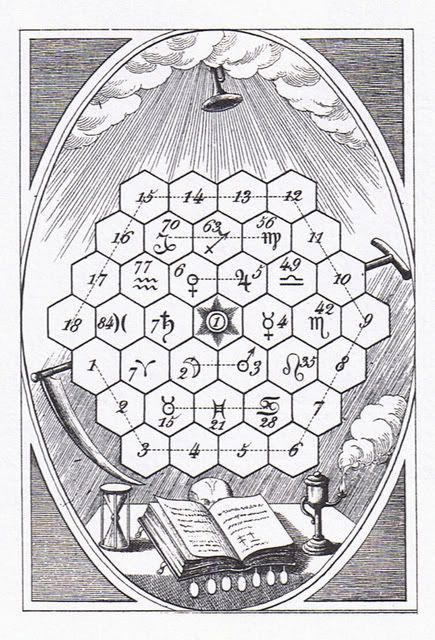 The Great Guide The Great GuideTake a look at the bottom of the image. Look familiar?  Zoroaster had 4 Oracles Zoroaster had 4 Oracles...I have written about one of them: http://kachina2012.wordpress.com/2008/07/08/37-solfeggio-zoroasters-oracles-seed-of-life/And I posted it on 2012Forum too: All about the patterns I noticed. The same archetypal patterns that keep reappearing. That can be recognized by the archetypal company they keep. The Chaldæan Oracles of Zoroasterby W. Wynn Westcott [1895] http://www.sacred-texts.com/eso/coz/index.htmAs some of you may know, Wynn Westcott and A.E. Waite and A. Crowley were buddies? Some of them were Freemasons. And the meditation room follows the BLACK Door pattern once again that we see used in St. Peter Square and The Shrine of the Book and even in Peru. Back in the opening post: Quote:
The U.N. Meditation Room (right) is built in the shape of a truncated pyramid. In the center is an altar made out of magnetite, the largest natural piece of magnetite ever mined. For meditation purposes it is probably the most ideal spot on the planet, since the magnetite altar has its foundation straight down, built into the bedrock of the land below; tapping into the energies of the earth itself. The mysterious mural also helps the worshippers tune into esoteric energies, and helps facilitate a state of altered consciousness.
And the Ka'ba stone in Mecca has 'magnetic' properties too??
namaste
_________________
KEY 528=Swastika=ancient Spherical Standing Wave Theory
“A theory is more impressive the greater is the simplicity of its premise, the more different are the kinds of things it relates and the more extended its range of applicability…”
-Einstein
http://2012forum.com/forum/viewtopic.php?f=15&t=13121&start=30 |
|
|
|
Rispondi |
Messaggio 268 di 455 di questo argomento |
|
|
EXAGONO=CUBO=37
QUE REPRESENTAN EN REALIDAD UN CUBO, EN UN CONTEXTO TRIDIMENCIONAL DE 64 CUBOS MAS CHICOS
AJEDREZ="EXPERIMENTO FILADELFIA"=APOCALIPSIS 3:7 |
|
|
|
Rispondi |
Messaggio 269 di 455 di questo argomento |
|

retomania.blogspot.com
de retos matemáticos donde
382 × 514 - 193k - png |

mailxmail.com
del espacio tridimensional
622 × 350 - 39k - jpg |

wordpress.colegio-arca...
En un espacio tridimensional,
832 × 601 - 90k - png |

hipertextual.com
gráficas tridimensionales
800 × 524 - 110k - jpg |

es.wikipedia.org
tridimensional[editar]
300 × 300 - 47k - png |

retomania.blogspot.com
Las letras que se observan en
516 × 540 - 184k - png |

joselorlop.blogspot.com
una versión tridimensional
1132 × 578 - 31k - png |

gaussianos.com
La cosa queda como se ve en
519 × 552 - 118k - png |

mailxmail.com
del espacio tridimensional
250 × 205 - 17k - jpg |

livedoc.4d.com
una fórmula matemática:
394 × 248 - 111k - png |

educarchile.cl
Ilustración del problema
300 × 228 - 6k - jpg |

gaussianos.com
Corazón en 3D
262 × 291 - 20k - jpg |

es.wikipedia.org
Tridimensional
220 × 184 - 7k - png |

educaplanet.com
3d Matemáticas vertices,
300 × 300 - 64k - png |

es.wikipedia.org
que es tridimensional.
350 × 114 - 30k - png |

circuitoselectronicos.org
Gráfica función una variable
500 × 290 - 26k - jpg |

mailxmail.com
Curso vídeo Matemáticas con
250 × 205 - 12k - jpg |

micromania.es
Taller U-tad - Matemáticas y
640 × 514 - 119k - jpg |

educapeques.com
tridimensionales 02
3120 × 2178 - 589k - jpg |

es.aliexpress.com
geometría tridimensional
750 × 867 - 128k - jpg |
|
|
|
|
Rispondi |
Messaggio 270 di 455 di questo argomento |
|
|
| Reply |
Message 24 of 24 on the subject |
|
El término cuarta dimensión aparece en diversos contextos como la física, las matemáticas y la ciencia ficción. En cada contexto el significado es diferente:
En física, se hace referencia a la cuarta dimensión al hablar del tiempo, principalmente desde el planteamiento de la Teoría de la Relatividad.
En matemática, el concepto aparece asociado o bien a espacios euclídeos de más de tres dimensiones o, más generalmente, a espacios localmente euclídeos o 4-variedades diferenciables.

Hipercubo de 4 dimensiones espaciales girando, tal como se vería proyectado en el espacio tridimensional.
El interés en las dimensiones más altas alcanzó su clímax entre 1870 y 1920.1 En esos años se convirtió en tema frecuente en la literatura fantástica, el arte e incluso algunas teorías científicas. La cuarta dimensión, entendida como dimensión espacial adicional (no como dimensión temporal, como en la teoría de la relatividad) apareció en las obras literarias de Oscar Wilde, Fiódor Dostoyevski, Marcel Proust, H. G. Wells y Joseph Conrad, inspiró algunas obras musicales de Alexander Scriabin, Edgar Varèse y George Antheil y algunas obras plásticas de Pablo Picasso y Marcel Duchamp influyendo en el desarrollo del cubismo. Incluso personajes tan diversos como el psicólogo William James, la escritora Gertrude Stein o el socialista revolucionario Vladimir Lenin se interesaron en el tema.
Igualmente los matemáticos habían estado interesados en el tema al tratar de generalizar los conceptos de la geometría euclídea tridimensional. El matemático Charles L. Dodgson, que enseñó en la Universidad de Oxford, deleitó a generaciones de escolares escribiendo libros, bajo el pseudónimo de Lewis Carroll, que incorporaban algunas ideas sobre la cuarta dimensión. Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann. Charles Howard Hinton, matemático y escritor de ciencia ficción británico, acuñó muchos neologismos para describir elementos en la cuarta dimensión. De acuerdo con el Oxford English Dictionary, fue el primero en emplear la palabra tesseract en su libro Una nueva era del pensamiento. También inventó las palabras “kata” (del griego “abajo”) y “ana” (del griego “arriba”) para describir las dos direcciones opuestas en la cuarta dimensión, equivalentes a derecha-izquierda, arriba-abajo, y adelante-atrás.
Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como "rotaciones" en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la "cuarta dimensión" no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.
Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un "espacio" de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.

Un ángulo recto se describe como un cuarto de una revolución. La Geometría Cartesiana escoge direcciones ortogonales arbitrariamente a través del espacio, lo que significa que cada dirección está en ángulo recto con las demás. Las 3 dimensiones ortogonales del espacio se conocen como altitud, longitud y latitud. La Cuarta Dimensión por lo tanto es la dirección en el espacio con ángulo recto a las 3 direcciones observables.
Un vector espacial es un conjunto de vectores, los cuales podemos imaginarlos como flechas, que proviene de un simple lugar llamado origen (vectores geométricos), que apuntan a otros lugares.
Un punto es un objeto de cero dimensiones. No tiene extensión en el espacio ni propiedades, como una flecha pero sin longitud. Este vector es llamado el vector cero y es el más simple vector espacial.
Una línea es un objeto unidimensional. Si escogemos un cierto vector distinto a cero en una cierta dirección, este vector tiene cierta longitud definida. Ese vector tiene una cabeza en un cierto punto en espacio y una cola en el origen. Si pensamos en estirar que ese vector así sea dos veces su largo, tres veces, etcétera y uniformemente, tomando todas las longitudes posibles (incluso la longitud cero, conseguir el vector cero), conseguiremos una sola línea con una sola dimensión: La de la longitud. Todos los vectores que describen puntos en esta línea serían paralelos. Aunque para visualizar la línea es necesario que ésta tenga un ancho mínimo, sin embargo, una línea de 1D no la tendría.
Un plano es un objeto de dos dimensiones. Tiene longitud y anchura pero no profundidad - algo como una hoja de papel, o más exactamente algo como las imágenes en un televisor común. El pensamiento en un plano en términos de vectores puede ser un poco más desafiante. Si pensamos en tomar un vector y lo movemos de modo que su cola esté tocando la cabeza del primero y esté formando un vector con su cola en el origen y la cabeza en la cabeza del segundo vector colocado de nuevo, tenemos una manera razonable de hablar de vectores de adición. Si tenemos dos vectores que no sean paralelos, podemos hablar de todos los puntos que podemos alcanzar por o solamente el estirar o ningunos de los vectores, y, agregando estos vectores juntos, estos puntos forman un plano.
El espacio, como lo percibimos, es tridimensional. Podemos pensar en poner una línea junto con un plano. Estas líneas son como un emparedado. Para conseguir a un cierto punto en espacio, podemos imaginarnos el viajar encima de la línea y después el movernos a través del plano al punto. Entonces tenemos tres vectores a pensar alrededor, uno a viajar una cierta distancia encima de la línea y dos para conseguir a un cierto punto en espacio.
Para tres rectas ortogonales en el espacio tridimensional (x, y y z) existe una cuarta, normal al espacio, ortogonal a estas tres rectas, que forma un eje p. ej. w.
El producto vectorial es la determinante de una matriz 4×4, donde una de las filas (o columnas) son los vectores unitarios h, i, j y k y las demás (filas o columnas respectivamente) están formadas por las componentes de tres vectores cuadradimensionales cualesquiera, este producto nos dará un cuarto vector perpendicular a estos tres mismos.
La Geometría euclidiana prevé una mayor variedad de formas para existir que en tres dimensiones. Los poliedros tridimensionales son recintos espaciales hechos de caras de dos dimensiones conectadas, los policronos cuadridimensionales son recintos del espacio cuadridimensional hechos de poliedros tridimensionales. Donde en tres dimensiones, hay exactamente cinco poliedros regulares, o los sólidos platónicos, que pueden existir, seis policronos regulares existen en la cuarta dimensión. Cinco de los seis se pueden interpretar como extensiones naturales de los sólidos platónicos, así como el cubo, un sólido platónico, es una extensión del cuadrado de dos dimensiones. El pentachoron está hecho de 5 tetraedros para las caras y 10 caras triangulares, y es el análogo cuadridimensional del tetraedro. El teseracto, o el hipercubo, se compone de 8 caras cúbicas y de 24 cuadrados, y es el politopo cuadridimensional medido. Los teseractos se doblan, la 16-celdas, son el equivalente del octaedro, pues son ambos politopos de cruz. Los politopos de 120 celdas y los de 600 celdas se doblan de igual modo, y son análogos al dodecaedro y al icosaedro, respectivamente. El de 24 celdas es un policrono regular único y que no tiene ningún equivalente tridimensional. Apenas pues la esfera, o 2-esfera, es una superficie de dos dimensiones curvada compuesta de todos los puntos equidistantes de un punto central dado, en un espacio tridimensional, la 3-esfera, una clase de hiperesfera, es el espacio que contiene todos los puntos equidistantes a un punto central dado, en un espacio cuadridimensional. Cada sección transversal tridimensional de un 3-esfera es un 2-esfera.

La analogía dimensional se usa frecuentemente para comprender el salto de una dimensión (en este caso, la tercera dimensión) a una más alta (cuarta dimensión). La analogía dimensional consiste en resolver un problema en n + 1 dimensiones relacionándolo primero con un problema análogo de (n - 1) dimensión, vale decir, "una dimensión menos". E igualmente debe analizarse el caso de cómo se relaciona el problema en n con el de (n + 1) dimensiones, es decir, "una más".
Edwin Abbott Abbott en su libro Planilandia (Flatland) escribe sobre un "ser cuadrado" que vive en un mundo de dos dimensiones, como la superficie de un pedazo de papel. Este "cuadrado" se enfrenta a experimentos de un ser tridimensional. El ser tridimensional es percibido por el "cuadrado" como un ser aparentemente divino, ya que puede poner y quitar objetos de una caja fuerte sin romperla ni abrirla (moviéndolos a través de su tercera dimensión), ver todo desde de la perspectiva de dos dimensiones sea incluido detrás de las paredes (puesto que ve "sobre" Planilandia), y totalmente invisible para los habitantes de Planilandia, puesto que está "arriba" y una dimensión por arriba de las dos dimensiones en las que el cuadrado está atrapado. No obstante, el ser tridimensional podría manifestarse en el mundo de dos dimensiones, pero sólo parcialmente, si fuera una esfera, aparecería como una secuencia de círculos sucesivos "que cambian de tamaño" (intersecciones de la esfera con el plano de dos dimensiones). Aplicando analogía dimensional, uno puede deducir que el ser cuadridimensional sería capaz de hazañas similares de nuestra perspectiva tridimensional.
Rudy Rucker demuestra esto en su novela "Spaceland", en la cual el protagonista encuentra los seres cuadridimensionales que demuestran tales energías. Un uso útil de la analogía dimensional en visualizar la cuarta dimensión está en la proyección. Una proyección es una manera para representar un objeto (n+1)-dimensional en la n-dimensión. Por ejemplo, las pantallas de computadora son de dos dimensiones, y todas las fotografías de objetos tridimensionales son representadas en dos dimensiones puesto que la información de la tercera dimensión (o de la profundidad) no puede ser representada por la pantalla (si el observador se mueve, aleje o acerque, la imagen no cambiará). En este caso, la profundidad se quita y se substituye por la información indirecta. La retina del ojo es un arsenal de dos dimensiones de receptores pero puede permitir que el cerebro perciba la naturaleza de objetos tridimensionales usando la información indirecta (como la perspectiva, el sombreado, visión binocular, etc.).
La perspectiva del uso de los artistas da profundidad tridimensional a los cuadros de dos dimensiones. Asimismo, los objetos en la cuarta dimensión se pueden proyectar matemáticamente a las familiares tres dimensiones, donde pueden entonces ser examinados más convenientemente. En este caso, la "retina de un ojo cuadridimensional" tendría un arsenal de receptores tridimensionales. El ser hipotético con tal ojo percibiría la naturaleza de objetos cuadridimensionales usando la información indirecta contenida en las imágenes que recibe en su retina. La proyección de la perspectiva a partir de cuatro dimensiones produce efectos similares como en el caso tridimensional, tal como la perspectiva.
Esto agrega "profundidad cuadridimensional" a estos cuadros tridimensionales. La analogía dimensional también ayuda a entender tales proyecciones. Por ejemplo, los objetos de dos dimensiones son limitados por límites unidimensionales: un cuadrado es limitado por cuatro bordes o líneas. Los objetos tridimensionales son limitados por superficies de bidimensionales: un cubo es limitado por 6 cuadrados. Aplicando analogía dimensional, uno puede deducir que un cubo cuadridimensional, conocido como teseracto, es limitado por los volúmenes tridimensionales.
Y de hecho, éste es el caso matemáticamente: el teseracto es limitado por 8 cubos. Saber esto es indispensable para entender cómo interpretar una proyección tridimensional del teseracto. Los límites del teseracto proyectan a los volúmenes en la imagen, superficies no simplemente de dos dimensiones. Esto ayuda a entender las características de dichas dimensiones que de otra manera sólo confundirían. De igual manera, el concepto de sombras puede ayudarnos mejor a entender la teoría de cuatro dimensiones. Si usted proyectara una luz sobre objeto tridimensional, éste proyectaría una sombra de dos dimensiones. Por lo tanto la luz en un objeto de dos dimensiones echaría una sombra unidimensional (en un mundo de dos dimensiones), y la luz en un objeto unidimensional en un mundo unidimensional echaría una sombra cero-dimensional, es decir, un punto de la no-luz. Esta idea se puede utilizar en la otra dirección; la luz en un objeto cuadridimensional proyectaría una sombra tridimensional. Como ejemplo, la sombra de un cubo transparente, proyectaría una sombra sobre el papel, de dos cuadrados, unidos por sus vértices con 4 segmentos.
Semejantemente, si era un cubo cuadridimensional iluminado con luz de 4 dimensiones, su sombra sería la de un cubo tridimensional dentro de otro cubo tridimensional. Siendo tridimensionales podemos solamente ver el mundo con nuestros ojos en dos dimensiones; el ser cuadridimensional consideraría el mundo en tres. Así podría, por ejemplo, ver los seis lados de una caja opaca simultáneamente. No solamente eso; también podría ver lo que hay al interior de la caja, como en Planilandia, en donde la esfera ve objetos en el mundo de dos dimensiones y todo dentro de ellos simultáneamente. Análogo, un espectador cuadridimensional vería todos los puntos en nuestro espacio tridimensional simultáneamente, incluyendo la estructura interna de objetos sólidos y de cosas obscurecidos de nuestro punto de vista.
Albert Einstein en su célebre teoría de 1905 de la relatividad especial habló por primera vez del tiempo como una cuarta dimensión y como algo indispensable para ubicar un objeto en el espacio y en un momento determinado. El tiempo en la teoría de la relatividad no es una dimensión espacial más, ya que fijado un punto del espacio-tiempo éste puede ser no alcanzable desde nuestra posición actual, hecho que difiere de la concepción usual de dimensión espacial. Aunque inicialmente se interpretó el tiempo como una "dimensión" matemática necesaria para ubicar un evento u objeto, en la teoría de la relatividad general el tiempo es tratado como una dimensión geométrica más, aunque los objetos materiales no puedan seguir una trayectoria completamente arbitraria a lo largo del tiempo (como por ejemplo "dar la vuelta" y viajar al pasado). La necesidad del tiempo dentro de la teoría de la relatividad es necesaria por dos motivos:
En primer lugar, los objetos no sólo se mueven a través del espacio sino que también lo hacen a través del tiempo, es decir su coordenada temporal aumenta continuamente, por lo que hubo la necesidad de hablar del tiempo ligado al espacio como la cuarta dimensión (en inglés spacetime, en castellano espacio-tiempo). Además el ritmo de avance en la dimensión temporal depende del estado de movimiento del observador, produciéndose una dilatación temporal efectiva para los observadores más rápidos en relación al tiempo medido por un observador estacionario.
En segundo lugar, el carácter intrínseco del espacio-tiempo y su cuatridimensionalidad requiere un modo conceptualmente diferente de tratar la geometría del universo, puesto que una cuarta dimensión implica un espacio plano (bidimensional) que se curva en la teoría de la relatividad general por la acción de la gravedad de la materia originándose la curvatura del espacio-tiempo.
Finalmente cabe añadir que algunas teorías físicas como la teoría de Kaluza-Klein y las teoría de supercuerdas, en sus varias versiones, añaden a las tres dimensiones físicas espaciales entre 1 y 9 dimensiones espaciales adicionales, de tipo compacto; además de la dimensión temporal.
|
|
|
|
|
|
Rispondi |
Messaggio 271 di 455 di questo argomento |
|
| Tanto el Tabernáculo y el Templo consistían de tres partes: |
| |
El Atrio |
El Lugar Santo |
El Lugar Santísimo |
|
Con relación al Tabernáculo
|
| |
El Lugar Santísimo era un cubo (10 pies x 10 pies x 10 pies) |
|
Con relación al Templo:
|
| |
El Lugar Santísimo era un cubo (20 pies x 20 pies x 20 pies) |
El tabernáculo propiamente dicho era una tienda cuadrangular, de 30 codos* de
largo, 10 de ancho y 10 de alto. Las dimensiones del conjunto de la estructura
no figuran con exactitud en los registros del Exodo, pero se las puede calcular
sobre la base de los detalles que se dan de las cortinas y las tablas que se
usaron en las paredes del tabernáculo, y de las medidas proporcionales, pero
mayores, del templo de Salomón (1 R. 6:2). La tienda estaba dividida en 2
compartimentos: el 1º conocido como "lugar santo" (Ex. 28:29), y el 2º como
"lugar santísimo", literalmente "el Santo de los Santos" (26:33, BJ). Este
constituía un cubo de 10 codos por lado, mientras el lugar santo era de 10
codos por 20. El tabernáculo estaba rodeado por un atrio o patio de 50 codos
de ancho por 100 de largo, limitado por cortinas de lino de 5 codos de alto
(27:18). Esta pared de cortinas estaba suspendida por 60 columnas, quizá de
maderas de acacia* (por ser esta la madera usada para los muebles y otras
columnas; cf 26:37) revestidas de plata y sostenidas por pedestales de bronce.
En la parte central del extremo oriental del patio se hallaba la entrada, que
estaba constituida por una cortina especial de 20 codos de largo (27:9-17). En
la mitad oriental del patio, cerca de la entrada, estaba el altar de los
holocaustos (vs 1-8) y el lavacro o lavatorio (30:17-21).
Leer más: Diccionario Biblico Cristiano Online y Gratis en Español - Significado o definicion de Tabernaculo
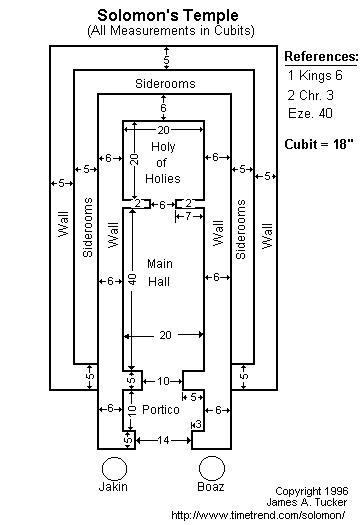
EL LUGAR SANTISIMO DEL TEMPLO DE SALOMON Y DEL TABERNACULO DE MOISES TENIA FORMA DE CUBO Y ESTABA ORIENTADO DE ESTE A OESTE. CONCRETAMENTE DICHO COMPARTIMENTO ESTABA HACIA ADONDE SALE LA LUNA CRECIENTE. ESTO EXPLICA SU FUERTE NEXO CIENTIFICO CON DICHA LUNA, INTERRELACIONADA CON EL NACIMIENTO DE UN NIÑO. LA LUNA CRECIENTE TIENE LA CUALIDAD DE QUE SALE Y SE PONE A LA PUESTA DEL SOL SIEMPRE EN EL OESTE. CONCRETAMENTE EL MENSAJE ESPIRITUAL DEL LUGAR SANTISIMO DEL TABERNACULO DE MOISES Y DEL TEMPLO DE SALOMON TIENE UN FUERTE NEXO, INSISTO CON EL NACIMIENTO DE UN NIÑO, Y MAXIME QUE EN EL CONTEXTO A LOS MESES DEL AÑO EL OESTE NOS CAE EN SEPTIEMBRE U OCTUBRE, OSEA EN LA FIESTA DE LOS TABERNACULOS. TABERNA/VINO/GRIAL
Si usted mira objetivamente el cubo vera que esta relacionado con el NUMERO 6 (6 SUPERFICIES), 12 (LINEAS PERIMETRALES/12 MESES LUNARES), NUMERO 8 (PUNTOS PERIMETRALES/RESURRECCION) E INCLUSO CON EL NUMERO 28 CONSIDERANDO LAS LINEAS DIAGONALES INCLUIDAS LAS INTERIORES. CONCRETAMENTE EL CUBO ESTA DISEÑADO EN FUNCION EL MES LUNAR CON LOS SABADOS LUNARES.
INCLUSO TAMBIEN LE VEMOS AL CUBO UN NEXO ZODIACAL Y GALACTICO EN EL CONTEXTO A LOS EXTREMOS DEL ZODIACO SEGUN APOCALIPSIS 4:7
HIPERCUBO
SI CONTAMOS LA CANTIDAD DE PARTES DEL CUBO MAGICO TENEMOS EL ASOMBROSO NUMERO 26 RELACIONADO CON LA GEMATRIA EN EL HEBREO DE YHWH E INCLUSO EN EL INGLES DE GOD/DIOS.
| god in Simple Gematria Equals: 26 |
( |
g
7 |
o
15 |
d
4 |
) |
APOCALIPSIS 21
15. El que hablaba conmigo tenía una caña de medir, de oro, para medir la ciudad, sus puertas y su muro.
16. La ciudad se halla establecida en cuadro, y su longitud es igual a su anchura; y él midió la ciudad con la caña, doce mil estadios; la longitud, la altura y la anchura de ella son iguales.
17. Y midió su muro, ciento cuarenta y cuatro codos, de medida de hombre, la cual es de ángel.
8 AÑOS SOLARES=13 PERIODOS SIDEREOS DE VENUS
16 AÑOS SOLARES=26 PERIODOS SIDEREOS DE VENUS
EN REALIDAD QUE LAS 12 HORAS DEL RELOJ, EN EL CONTEXTO A LA ESTRELLA DE DAVID (12 HORAS) Y EN EL CONTEXTO AL EXAGONO EN LA MISMA (NUMERO 13=SANTA CENA) TIENE ESTA CONNOTACION.
ESTE ES EL SECRETO DE LA RELACION DE LA GEMATRIA DE YHWH CON EL NUMERO 26.
|
|
|
|
Rispondi |
Messaggio 272 di 455 di questo argomento |
|
| Reply |
Message 219 of 219 on the subject |
|
|
|
|
|
|
|
|
Rispondi |
Messaggio 273 di 455 di questo argomento |
|
The number 512 has alot to do with 256. Could they connect to 137?
512 does look like SIN when rearranged to letters. In number theory 512 is a Leyland number.
In the Hellenistic period, the ratio 256:153 was used as an approximation of the square root of 3.
If the number 153 represents the width of the vesica pisces of the net, then the value is 256 for the height of the vesica pisces.
 http://omegafoundation.siriuscomputing.net/Education/John21.htm http://omegafoundation.siriuscomputing.net/Education/John21.htm
It also in an important triangular & cubical number.
512 channel's in the cube each with 256 setting's 
256+256=512
Cube 8 x 8 x 8 (64x8) = 512 cubes

There are 24 cubes organized into 3 groups of 8 that get cut perpendicular among themselves.
The I Ching is a chess board that is 8x8, divided in 64 smaller cubes with each consisting of 6 bits. If we multiplied another 8 into this board, then it becomes 8x8x8, 1 cube divided in 512 smaller cubes.
Each cube is conformed by 6 faces & each one recorded with 6 bits, then we have 6 faces/cube x 6 bits/cube= 36 bits/cube.
512 cubes x 36 bits a cube = 18432 bits
Relating this to Mahavairocana's mandala, we have the 36 human figures surrounding Mahavairocana.
There are 24 petals organized in 3 groups of 8 surrounding Mahavairocana.
8+8+8= 24 CranIEL nerves (12 for each hemisphere of the brain)
Gold nano clusters don't get any larger than 24 atoms. 
http://www.eurekalert.org/multimedia/pub/2871.php?from=89175
| Quote: |
Using Pythagoras' ratios of 2:1, 3:2, and 5:4, you can tune most of the notes on a scale.
256 Hz for middle C (which is how some computer speakers are tuned)
Then an octave above middle C is 2 * 256 Hz = 512 Hz, and an octave below middle C is 1/2 * 256 Hz = 128 Hz |
512 is the cube of 8x8x8 with 6 sides & 8x8x8 triangles each of 36 (6x6x6) = 512
Going back to Ifa divination, there are 16 major books in the Odu Ifa literary corpus. When combined there are total of 256 Odu.
(a collection of 16, each of which has 16 alternatives (16^2, or 4^4)
Could 512/256/64 be a larger picture of our cos mos & our internal structure 
256 characters max in all aplications 
The number of 'Jesus' & 'Logos' is 888.
888 = HHH
8x8x8 = 8Fold Path of Buddha (Dharma) 
 http://gnosticteachings.org/books-by-samael-aun-weor/the-aquarian-message/1181-the-seven-vials-are-poured.html http://gnosticteachings.org/books-by-samael-aun-weor/the-aquarian-message/1181-the-seven-vials-are-poured.html
_________________
TRIA SUNT MIRABILIA DEUS ET HOMO MATER ET VIRGO TRINUS ET UNUS
http://breakfornews.com/forum/viewtopic.php?t=5916&postdays=0&postorder=asc&start=132&sid=24dd1c2b90874d2553e783ac6084a452
|
|
|
|
Rispondi |
Messaggio 274 di 455 di questo argomento |
|
IF you are suspect of the info presented thus far
 http://2012forum.com/forum/viewtopic.php?f=15&t=13121&start=90 http://2012forum.com/forum/viewtopic.php?f=15&t=13121&start=90
please explain the mystery surrounding the number 55 and all of the profound temple associations linked together by this number or are they letters, or are they neither?
The number 55 can be associated to the Holy Spirit, the I Ching, the Kaaba Stone in Mecca, DNA ATCG, Stonehenge, and now the GREAT PYRAMID's Grand Gallery?
 http://2012forum.com/forum/viewtopic.php?p=338141#p338141 http://2012forum.com/forum/viewtopic.php?p=338141#p338141
THE CUBE of SPACE and the TAROT
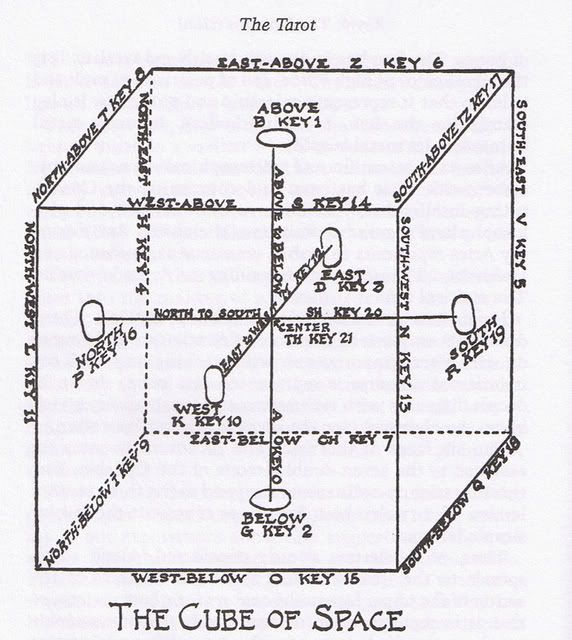
The CUBE has 32 paths comprised of 22 Hebrew Consonants plus the 10 Sephiroth that form the Tree of Life structure.
And please note that path #32 in the Tree of Life OR Cube is associated with the number 528.
Here is a quote from Stonehenge explorer Gerald Hawkins regarding those numbers above...
"....Stonehenge was locked to the sun and moon as tightly as the tides.
Those astonishing figures fairly haunted me: 22 key earthly positions aligning, 32 times, with 15 of the 18 unique sun/moon positions."
namaste
SS/55
_________________
KEY 528=Swastika=ancient Spherical Standing Wave Theory
“A theory is more impressive the greater is the simplicity of its premise, the more different are the kinds of things it relates and the more extended its range of applicability…”
-Albert Einstein
http://breakfornews.com/forum/viewtopic.php?t=5916&postdays=0&postorder=asc&start=12&sid=9523915082acbe9bc5271a5e4f1f8cf0
|
|
|
|
Rispondi |
Messaggio 275 di 455 di questo argomento |
|
1379 and another direct hit!
Here are a couple of quotes, an image and the link.
| Quote: |
The Lamp by Vernon Jenkins
Clearly, 37 and its companion 91 - both remarkable as numbers per se, as we have seen - feature strongly in the first eight words of the Scriptures! However, the account is not complete for we have yet to consider the numerical implications of the Creator's name as it is rendered in the Greek, nominative case, of both Septuagint and New Testament:
5 - A summary of N-R
The foregoing account identifies 37 and 91 as trifigurate numbers. In other words, each may be represented as a symmetrical arrangement of uniform counters in three distinct ways: 37, as hexagon, hexagram and octagon; 91, as triangle, hexagon and pyramid. This shared attribute of trifiguracy is neither bettered nor matched by any other natural number! Furthermore, 37 and 91 are related as difference and sum, respectively, of the cubes of 3 and 4.
In a denary context (familiar to all!) - and particularly in association with 3 and its multiples - this relationship is extended, and gives rise to many eye-catching curiosities that are particularly appealing to those seeking recreation through numbers. No other number, in this context, offers anything approaching the same degree of interest!
These observations are augmented by information from another quarter: Mr. J. Iuliano has drawn this author's attention to the following:
the number 37 is rooted in the double periodic modular forms of Fermat's Last Theorem;
an expression of the fine structure constant - ie the amplitude of an electron to emit or absorb a photon - involves 37, thus:

 http://freespace.virgin.net/vernon.jenkins/Symb.htm http://freespace.virgin.net/vernon.jenkins/Symb.htm
|
namaste
_________________
KEY 528=Swastika=ancient Spherical Standing Wave Theory
“A theory is more impressive the greater is the simplicity of its premise, the more different are the kinds of things it relates and the more extended its range of applicability…”
-Albert Einstein
http://breakfornews.com/forum/viewtopic.php?t=5916&postdays=0&postorder=asc&start=24&sid=efc5514d0281c68011e0ec73242201e6
|
|
|
 Primo Primo
 Precedente
261 a 275 de 455
Successivo Precedente
261 a 275 de 455
Successivo Ultimo
Ultimo
|

