2. A geometric derivation of the golden ratio

The following diagrams depict a regular pentagon - i.e. one whose vertices lie on a circle and whose sides and diagonals form isosceles triangles. Observe that each number represented is an angle expressed in degree measure.

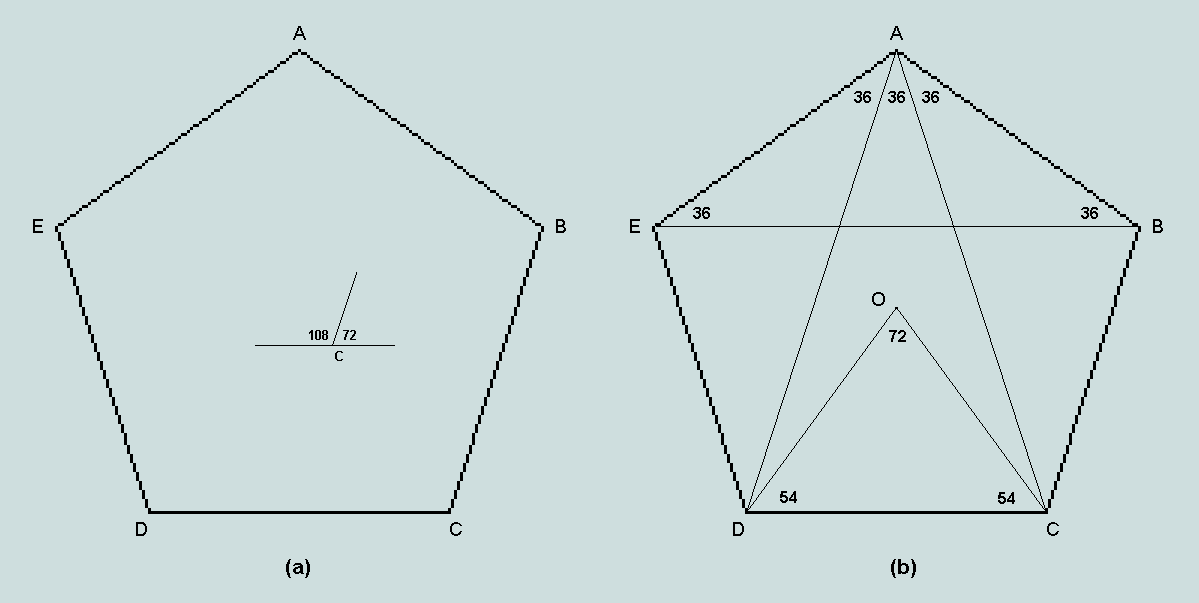
Since each exterior angle of the pentagon is 360/5, or 72, it follows that each interior angle is (180 - 72), or 108 [see inset at (a)]. At (b), O represents the centre of the circumscribed circle. Angle DAC is half the angle subtended at the centre - its value is therefore 36. The remaining angles are readily calculated - significantly, all are multiples of 18.

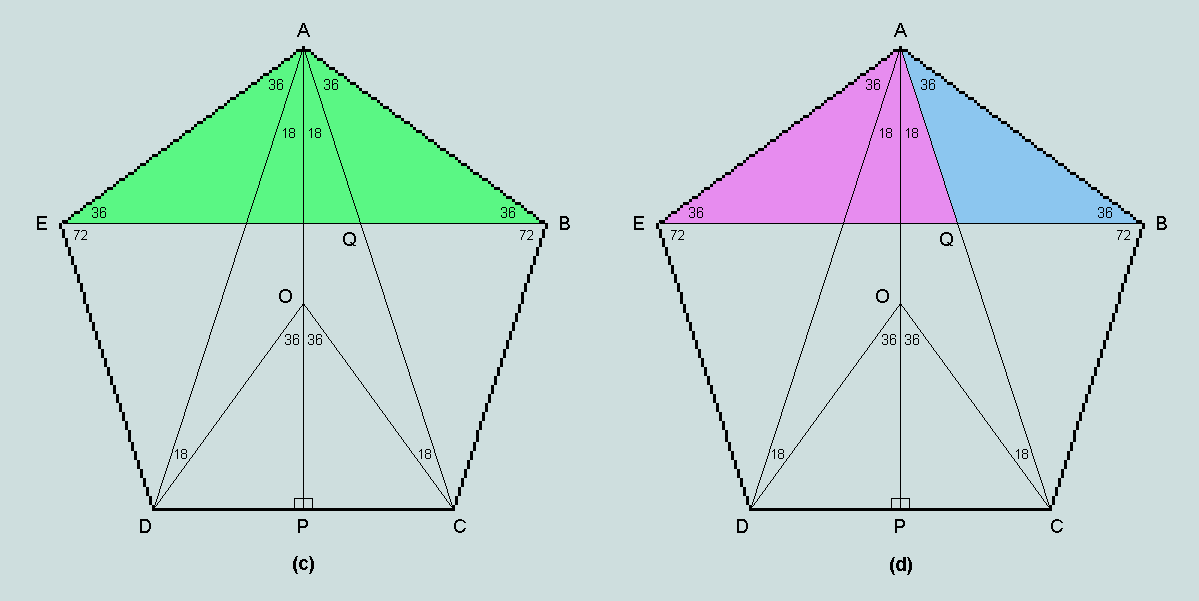
In the following developments, each of the coloured triangles is observed to be isosceles, and the green and blue triangles, similar. Thus, in particular,

EB/BA = BA/QB, whence

BA² = EB.QB

= (EQ + QB).QB = (AE + QB).QB

= (BA + QB).QB

 

It therefore follows that

BA/QB = (BA + QB)/BA = 1 + QB/BA

and, setting the ratio BA/QB = x, we have

x = 1 + 1/x, or x² = x + 1

whence,

x = (1 + 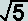) / 2 = 1.618034... = f, the GOLDEN RATIO ---------------- (iv)

 

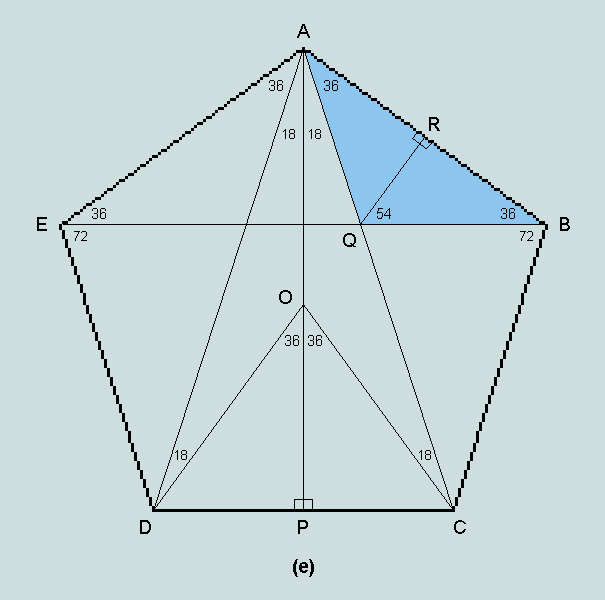
If the perpendicular, QR, now be dropped from Q onto AB (as in the diagram below), it follows that

BR/QB = f/2 = cos 36 = sin 54 -------------- (v)

Because the trigonometric functions are periodic, these results extend to limitless sequences of angles - as the following diagrams make clear.

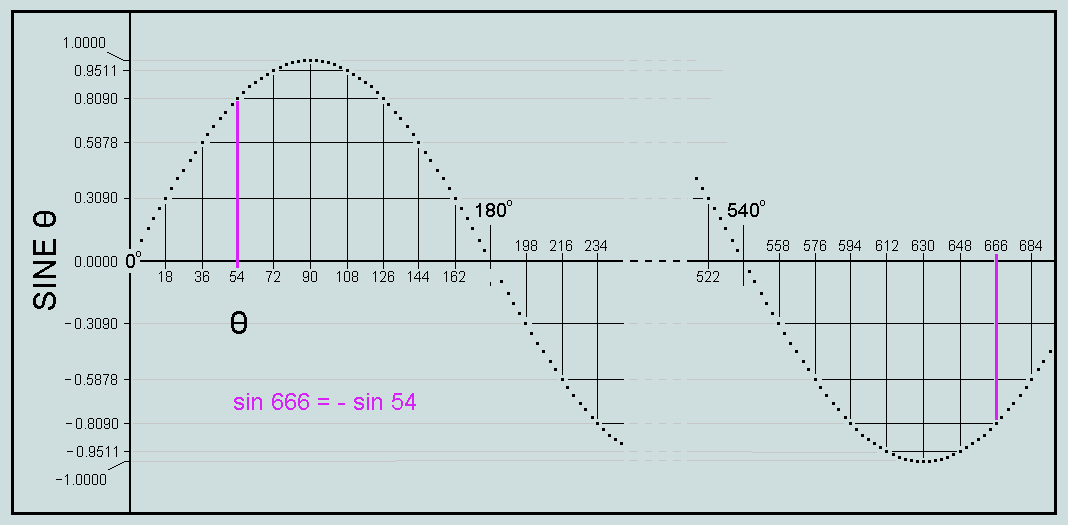
The outline of a typical sine curve is here represented by a series of points, q being a multiple of 3. Observe that the graduations on the axes refer to q a multiple of 18. Clearly, sin 54 = sin 126 = -sin 234...= -sin 594 = -sin 666 =...

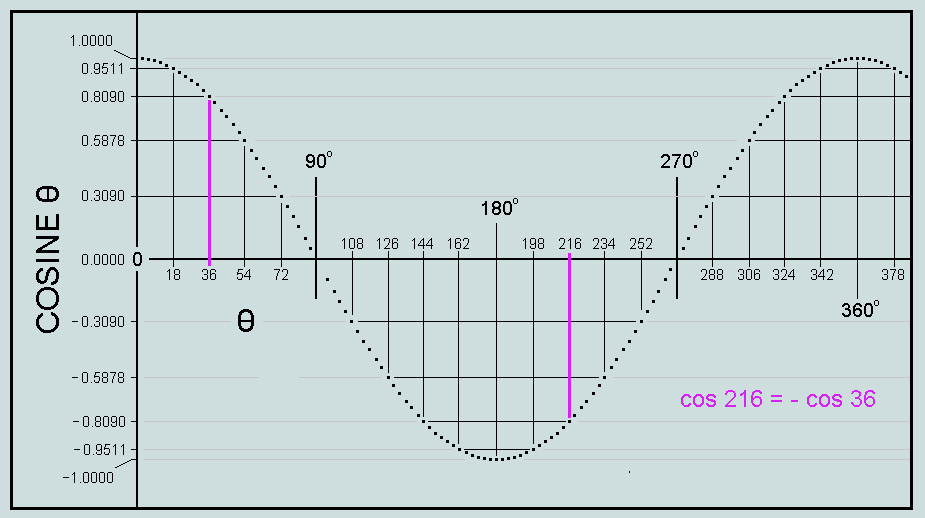
The corresponding cosine curve above similarly reveals cos 36 = -cos 144 = -cos 216 = cos 324 =...

Combining these observations therefore enables us to write

sin 666 + cos 216 = -f

whence,

f = - [sin (666) + cos (6.6.6)] ------------- (vi)

And what of 18, i.e. (6+6+6)? The following analysis shows that this angle too has a place in these proceedings. Here is the geometrical basis of the matter:

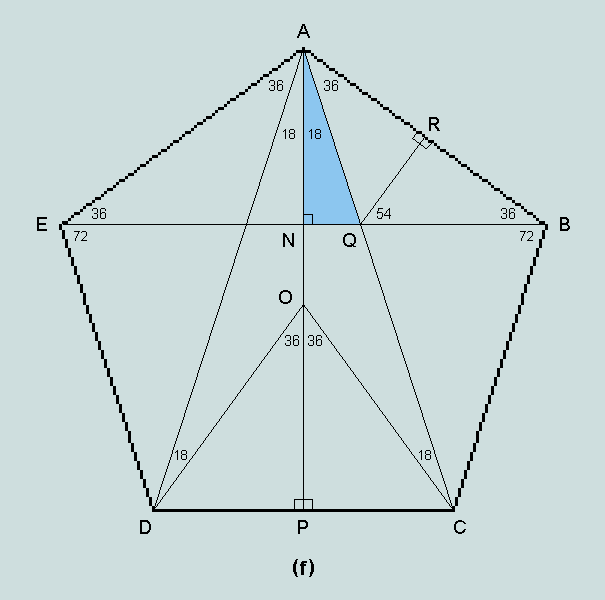
In triangle ANQ, sin 18 = NQ/QA = NQ/QB [triangle QBA isosceles] ----------------- (vii)

In triangle NBA, NB/BA = cos 36 = f/2 [from (v)], and

in triangle QBR, BR/QB = BA/(2.QB) = sin 54 = f/2 [from (v)]

Hence, NB = BA.f/2 and QB = BA/f

Clearly, therefore, NQ = NB - QB = BA.(f/2 - 1/f) = BA.(f² - 2)/(2.f) and it follows from (vii) that

sin 18 = BA.(f²- 2)/2.f) / (BA/f)

= (f² - 2)/2 = 1/(2.f) [since, from (ii) and (iii), f² = f + 1, and f - 1 = 1/f]

Whence,

f = cosec(18)/2 = cosec (6+6+6)/2 ---------------- (viii)

[Observe that each of the foregoing results - linking the golden section (f) with trigonometrical functions of particular angles - may be readly confirmed if one has access to a scientific electronic calculator.]