Página principal  |  Contato  

Correio eletrónico:

Palavra-passe:

Registrar-se agora!

Esqueceu-se da palavra-passe?
DESENMASCARANDO LAS FALSAS DOCTRINAS
 
Novidades
  Entre agora
  Painel de mensagens 
  Galeria de imagens 
 Arquivos e documentos 
 Inquéritos e Testes 
  Lista de participantes
 YHWH (DIOS PADRE) EL UNICO DIOS 
 JESUCRISTO NUESTRO MESIAS JUDIO 
 LOS DIEZ MANDAMIENTOS DE LA BIBLIA 
 MEJORE SU CARACTER Y SU VIDA 
 YOU TUBE-MAOR BA OLAM-LINKS 
 YOU TUBE-MAOR BA OLAM-LINKS II 
 BIBLIAS/CONCORDANCIA/LIBROS 
 MAYOR ENEMIGO DEL HOMBRE ES UNO MISMO 
 ¿LA TORA ES MACHISTA? -MENSAJE ESOTERICO Y EXOTERICO 
 ¿ES INMORTAL EL ALMA?- FALACIA DE LA ENCARNACION Y REENCARNACION 
 EL ISLAM TIENE ORIGEN UNITARIO ADOPCIONISTA 
 ANTIGUO TESTAMENTO-ESTUDIO POR VERSICULOS 
 NUEVO TESTAMENTO-ESTUDIOS POR VERSICULOS 
 NUEVO TESTAMENTO II-ESTUDIOS POR VERSICULOS 
 NUEVO TESTAMENTO III-ESTUDIOS POR VERSICULOS 
 CRISTO NO TUVO PREEXISTENCIA 
 ¿QUE ES EL ESPIRITU SANTO? 
 
 
  Ferramentas
 
ASTROTEOLOGIA-EVANGELIO EN LAS ESTRELLAS: July 4 is aphelion
Escolher outro painel de mensagens
Assunto anterior  Assunto seguinte
Resposta  Mensagem 1 de 97 no assunto 
De: BARILOCHENSE6999  (Mensagem original) Enviado: 24/08/2012 17:42

Earth Rotation and Revolution

The term Earth rotation refers to the spinning of our planet on its axis. Because of rotation, the Earth's surface moves at the equator at a speed of about 467 m per second or slightly over 1675 km per hour. If you could look down at the Earth's North Pole from space you would notice that the direction of rotation is counter-clockwise (Figure 6h-1). The opposite is true if the Earth is viewed from the South Pole. One rotation takes exactly twenty-four hours and is called a mean solar day. The Earth’s rotation is responsible for the daily cycles of day and night. At any one moment in time, one half of the Earth is in sunlight, while the other half is in darkness. The edge dividing the daylight from night is called the circle of illumination. The Earth’s rotation also creates the apparent movement of the Sun across the horizon.

Figure 6h-1: The movement of the Earth about its axis is known as rotation. The direction of this movement varies with the viewer’s position. From the North Pole the rotation appears to move in a counter-clockwise fashion. Looking down at the South Pole the Earth’s rotation appears clockwise.

 

The orbit of the Earth around the Sun is called an . This celestial motion takes 365.26 days to complete one cycle. Further, the Earth's orbit around the Sun is not circular, but oval or elliptical (see Figure 6h-2). An elliptical orbit causes the Earth's distance from the Sun to vary over a year. Yet, this phenomenon is not responsible for the Earth’s seasons! This variation in the distance from the Sun causes the amount of solar radiation received by the Earth to annually vary by about 6%. Figure 6h-2 illustrates the positions in the Earth’s revolution where it is closest and farthest from the Sun. On January 3, , the Earth is closest to the Sun (147.3 million km). The Earth is farthest from the Sun on July 4, or (152.1 million km). The average distance of the Earth from the Sun over a one-year period is about 149.6 million km.aphelionEarth revolutionperihelion

Figure 6h-2: Position of the equinoxes, solstices, aphelion, and perihelion relative to the Earth's orbit around the Sun.

 

Tilt of the Earth's Axis

The ecliptic plane can be defined as a two-dimensional flat surface that geometrically intersects the Earth's orbital path around the Sun. On this plane, the Earth's axis is not at right angles to this surface, but inclined at an angle of about 23.5° from the perpendicular. Figure 6h-3 shows a side view of the Earth in its orbit about the Sun on four important dates: June solstice, September equinox, December solstice, and March equinox. Note that the angle of the Earth's axis in relation to the ecliptic plane and the North Star on these four dates remains unchanged. Yet, the relative position of the Earth's axis to the Sun does change during this cycle. This circumstance is responsible for the annual changes in the height of the Sun above the horizon. It also causes the seasons, by controlling the intensity and duration of sunlight received by locations on the Earth. Figure 6h-4 shows an overhead view of this same phenomenon. In this view, we can see how the circle of illumination changes its position on the Earth’s surface. During the two equinoxes, the circle of illumination cuts through the North Pole and the South Pole. On the June solstice, the circle of illumination is tangent to the Arctic Circle (66.5° N) and the region above this latitude receives 24 hours of daylight. The Arctic Circle is in 24 hours of darkness during the December solstice.

Figure 6h-3:The Earth’s rotational axis is tilted 23.5° from the red line drawn perpendicular to the ecliptic plane. This tilt remains the same anywhere along the Earth’s orbit around the Sun. Seasons are appropriate only for the Northern Hemisphere.

 

Figure 6h-4: Annual change in the position of the Earth in its revolution around the Sun. In this graphic, we are viewing the Earth from a position in space that is above the North Pole (yellow dot) at the summer solstice, the winter solstice, and the two equinoxes. Note how the position of the North Pole on the Earth's surface does not change. However, its position relative to the Sun does change and this shift is responsible for the seasons. The red circle on each of the Earths represents the Arctic Circle (66.5 degrees N). During the June solstice, the area above the Arctic Circle is experiencing 24 hours of daylight because the North Pole is tilted 23.5 degrees toward the Sun. The Arctic Circle experiences 24 hours of night when the North Pole is tilted 23.5 degrees away from the Sun in the December solstice. During the two equinoxes, the circle of illumination cuts through the polar axis and all locations on the Earth experience 12 hours of day and night. Seasons are appropriate only for the Northern Hemisphere.

 http://www.physicalgeography.net/fundamentals/6h.html



Primeira  Anterior  2 a 7 de 97  Seguinte   Última 
Resposta  Mensagem 2 de 97 no assunto 
De: BARILOCHENSE6999 Enviado: 24/08/2012 17:43

On June 21 or 22 the Earth is positioned in its orbit so that the North Pole is leaning 23.5° toward the Sun (Figures 6h-3, 6h-4, 6h-5 and see animation - Figure 6h-7). During the June solstice (also called the in the Northern Hemisphere), all locations north of the equator have day lengths greater than twelve hours, while all locations south of the equator have day lengths less than twelve hours (see Table 6h-2). On December 21 or 22 the Earth is positioned so that the South Pole is leaning 23.5 degrees toward the Sun (Figures 6h-3, 6h-4, 6h-5 and see animation - Figure 6h-8). During the December solstice (also called the in the Northern Hemisphere), all locations north of the equator have day lengths less than twelve hours, while all locations south of the equator have day lengths exceeding twelve hours (see ).winter solsticesummer solsticeTable 6h-2

Figure 6h-5: During the June solstice the Earth's North Pole is tilted 23.5 degrees towards the Sun relative to the circle of illumination. This phenomenon keeps all places above a latitude of 66.5 degrees N in 24 hours of sunlight, while locations below a latitude of 66.5 degrees S are in darkness. The North Pole is tilted 23.5 degrees away from the Sun relative to the circle of illumination during the December solstice. On this date, all places above a latitude of 66.5 degrees N are now in darkness, while locations below a latitude of 66.5 degrees S receive 24 hours of daylight.

 

On September 22 or 23, also called the in the Northern Hemisphere, neither pole is tilted toward or away from the Sun (Figures 6h-3, 6h-4, 6h-6 and see ). In the Northern Hemisphere, March 20 or 21 marks the arrival of the or when once again the poles are not tilted toward or away from the Sun. Day lengths on both of these days, regardless of latitude, are exactly 12 hours.vernal equinoxautumnal equinoxspringanimation - Figure 6h-9

Figure 6h-6: During the equinoxes, the axis of the Earth is not tilted toward or away from the Sun and the circle of illumination cuts through the poles. This situation does not suggest that the 23.5 degree tilt of the Earth no longer exists. The vantage point of this graphic shows that the Earth's axis is inclined 23.5 degrees toward the viewer for both dates (see Figures 6h-3 and 6h-4). The red circles shown in the graphic are the Arctic Circle.

 

Axis Tilt and Solar Altitude

The annual change in the relative position of the Earth's axis in relationship to the Sun causes the height of the Sun or solar altitude to vary in our skies. Solar altitude is normally measured from either the southern or northern point along the horizon and begins at zero degrees. Maximum solar altitude occurs when the Sun is directly overhead and has a value of 90°. The total variation in maximum solar altitude for any location on the Earth over a one-year period is 47° (Earth’s tilt 23.5° x 2 = 47°). This variation is due to the annual changes in the relative position of the Earth to the Sun. At 50 degrees North, maximum solar altitude varies from 63.5 degrees on the June solstice to 16.5 degrees on the December solstice (Figure 6h-10). Maximum solar height at the equator goes from 66.5 degrees above the northern end of the horizon during the June solstice, to directly overhead on the September equinox, and then down to 66.5 degrees above the southern end of the horizon during the December solstice (Figure 6h-11).

Figure 6h-10: Variations in solar altitude at solar noon for 50 degrees North during the June solstice, equinox, and December solstice.

 

Figure 6h-11: Variations in solar altitude at solar noon for the equator during the June solstice, equinox, and December solstice.

 

The location on the Earth where the Sun is directly overhead at solar noon is known as the subsolar point. The subsolar point occurs on the equator during the two equinoxes (Figures 6h-11 and 6h-12). On these dates, the equator is lined up with the ecliptic plane and the poles are in line with the circle of illumination (Figure 6h-6). During the summer solstice, the subsolar point moves to the Tropic of Cancer (23.5° N) because at this time the North Pole is inclined 23.5° toward the Sun (Figures 6h-12 and 6h-13). Figure 6h-13 shows how the subsolar point gradually changes from one day to the next over a period of one-year. Note that on this graph, the subsolar point is located at the Tropic of Capricorn (23.5° S) during the December solstice when the South Pole is angled 23.5° toward the Sun (Figure 6h-5).


Resposta  Mensagem 3 de 97 no assunto 
De: BARILOCHENSE6999 Enviado: 24/08/2012 17:44
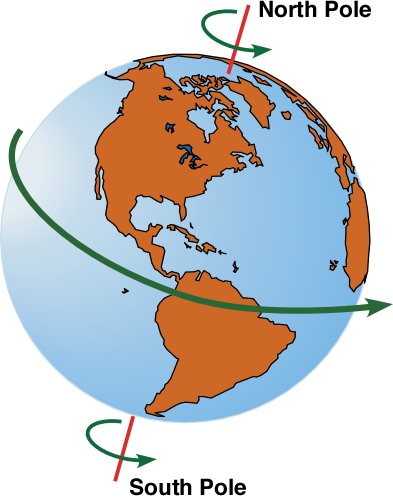
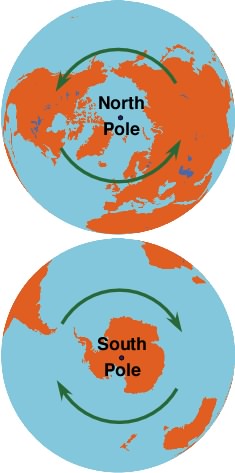
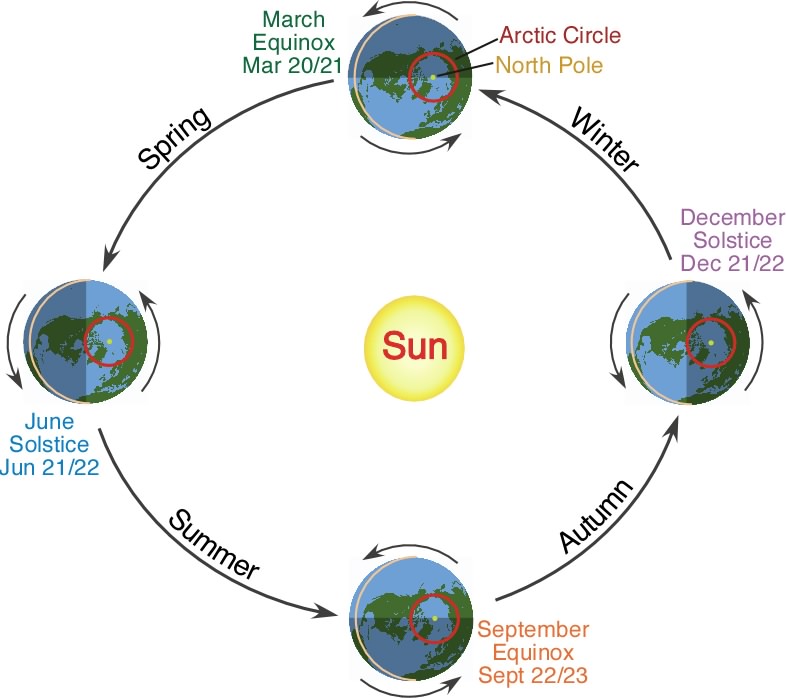
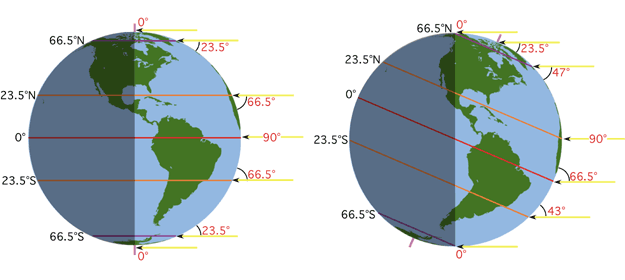
Figure 6h-12: Relationship of maximum Sun height to latitude for the equinox (left) and June solstice (right). The red values on the right of the globes are maximum solar altitudes at solar noon. Black numbers on the left indicate the location of the Equator, Tropic of Cancer (23.5 degrees N), Tropic of Capricorn (23.5 degrees S), Arctic Circle (66.5 degrees N), and the Antarctic Circle (66.5 degrees S). The location of the North and South Poles are also identified. During the equinox, the equator is the location on the Earth with a Sun angle of 90 degrees for solar noon. Note how maximum Sun height declines with latitude as you move away from the Equator. For each degree of latitude traveled maximum Sun height decreases by the same amount. At equinox, you can also calculate the noon angle by subtracting the location's latitude from 90. During the summer solstice, the Sun is now directly overhead at the Tropic of Cancer. All locations above this location have maximum Sun heights that are 23.5 degrees higher from the equinox situation. Places above the Arctic Circle are in 24 hours of daylight. Below the Tropic of Cancer the noon angle of the Sun drops one degree in height for each degree of latitude traveled. At the Antarctic Circle, maximum Sun height becomes 0 degrees and locations south of this point on the Earth are in 24 hours of darkness.

 

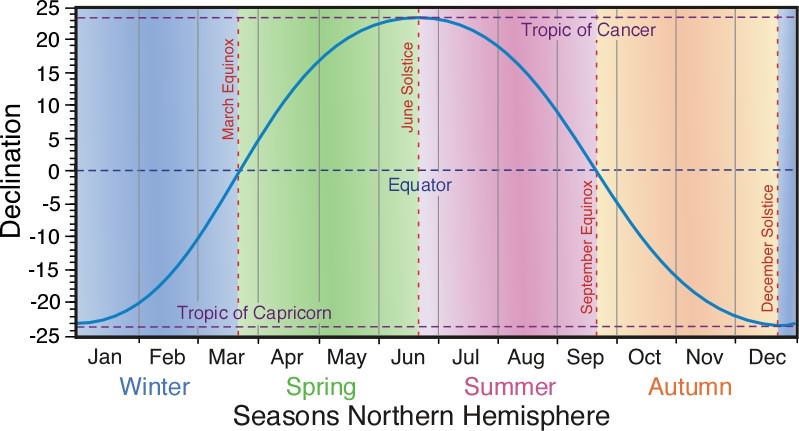
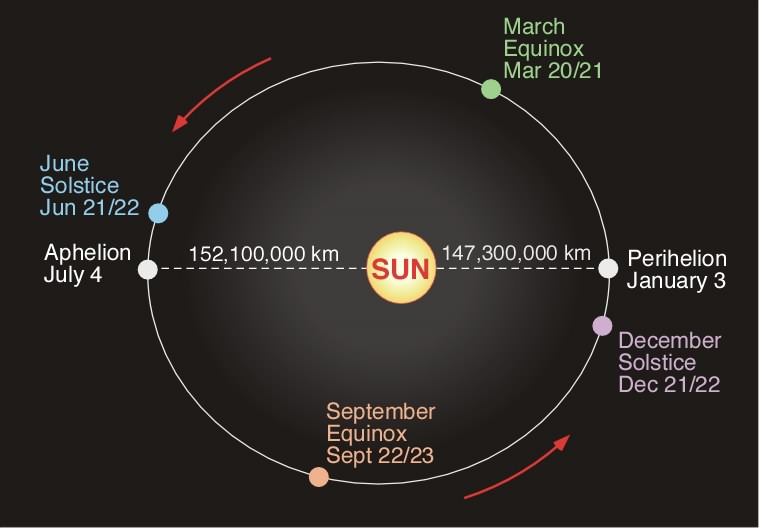
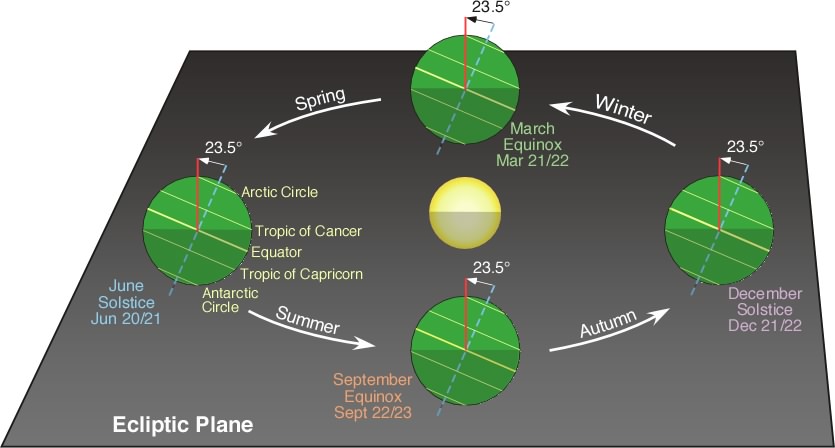
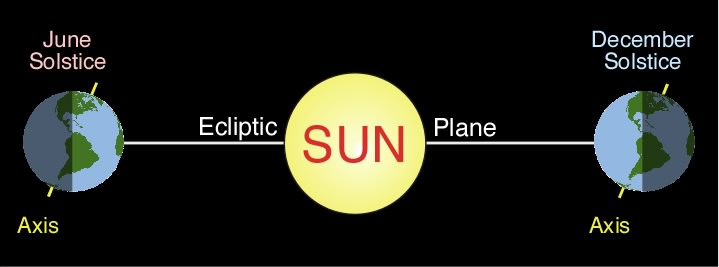
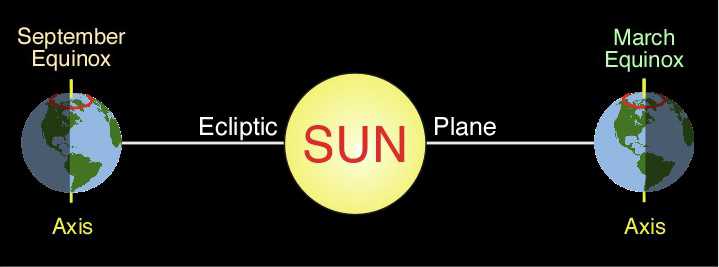
Figure 6h-13: Angle of the Sun’s declination and latitude of the subsolar point throughout the year. Seasons are for the Northern Hemisphere.

 

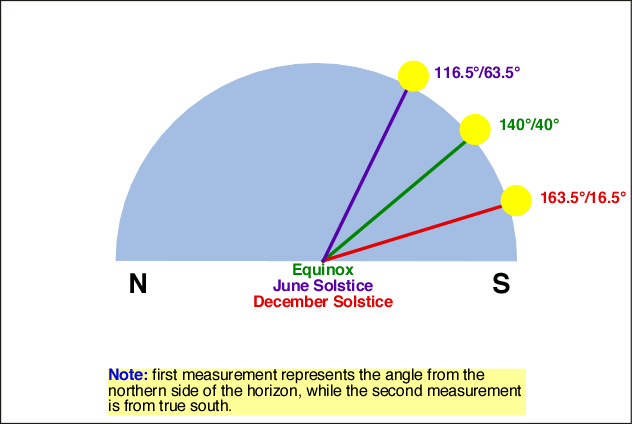
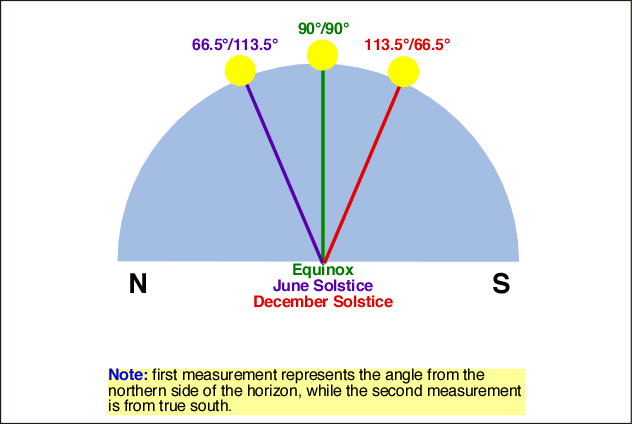
The following table describes the changes in solar altitude at solar noon for the two solstices and equinoxes. All measurements are in degrees (horizon has 180 degrees from True North to True South) and are measured from either True North or True South (whatever is closer).

 

Table 6h-1: Maximum Sun altitudes for selected latitudes during the two solstices and equinoxes.

Location's

Latitude

March Equinox

March 20/21

June Solstice

June 21/22

September Equinox

September 22/23

December Solstice

December 21/22

 90 N  0 degrees  23.5 degrees  0 degrees  - 23.5 degrees
 70 N  20 degrees  43.5 degrees  20 degrees  -3.5 degrees
 66.5 N  23.5 degrees  47 degrees  23.5 degrees  0 degrees
 60 N  30 degrees  53.5 degrees  30 degrees  6.5 degrees
 50 N  40 degrees  63.5 degrees  40 degrees  16.5 degrees
 23.5 N  66.5 degrees  90 degrees  66.5 degrees  43 degrees
 0 degrees  90 degrees  66.5 degrees  90 degrees  66.5 degrees
 23.5 S  66.5 degrees  43 degrees  66.5 degrees  90 degrees
 50 S  40 degrees  16.5 degrees  40 degrees  63.5 degrees
 60 S  30 degrees  6.5 degrees  30 degrees  53.5 degrees
 66.5 S  23.5 degrees  0 degrees  23.5 degrees  47 degrees
 70 S  20 degrees  -3.5 degrees  20 degrees  43.5 degrees
 90 S  0 degrees  - 23.5 degrees  0 degrees  23.5 degrees

 

 

The following links show graphical illustrations of the annual movements of the Sun in our skies for selected latitudes. In these illustrations, solar angles are measured from both True North and True South for solar noon.

 

| 90 N | 66.5 N | 50 N | 23.5 N | Equator (0) | 23.5 S | 50 S | 66.5 S | 90 S |

 

Finally, the altitude of the Sun at solar noon can also be calculated with the following simple equation:

 

Altitude A = 90 - Latitude L +/- Declination D

In this equation, L is the latitude of the location in degrees and D is the declination. The equation is simplified to A = 90 - L if Sun angle determinations are being made for either equinox date. If the Sun angle determination is for a solstice date, declination (D) is added to latitude (L) if the location is experiencing summer (northern latitudes = June solstice; southern latitudes = December solstice) and subtracted from latitude (L) if the location is experiencing winter (northern latitudes = December solstice; southern latitudes = June solstice). All answers from this equation are given relative to True North for southern latitudes and True South for northern latitudes. For our purposes only the declinations of the two solstices and two equinoxes are important. These values are: June solstice D=23.5, December solstice D=23.5, March equinox D=0, and Septemeber equinox D=0. When using the above equation in tropical latitudes, Sun altitude values greater than 90 degrees may occur for some calculations. When this occurs, the noonday Sun is actually behind you when looking towards the equator. Under these circumstances, Sun altitude should be recalculated as follows:

Altitude A = 90 - (originally calculated Altitude A - 90)

 
 
 

Study Guide
 

Additional Readings
 
Internet Weblinks
 
Citation: Pidwirny, M. (2006). "Earth-Sun Geometry". Fundamentals of Physical Geography, 2nd Edition. Date Viewed. http://www.physicalgeography.net/fundamentals/6a.html

Resposta  Mensagem 4 de 97 no assunto 
De: BARILOCHENSE6999 Enviado: 24/08/2012 17:47
  1.  
     

    Earth at Aphelion

    spaceweather.com/glossary/aphelion.htmlEn caché - Traducir esta página
    On July 4, 2008, our planet is at the distant end--a point astronomers call " aphelion." This puts us farther from the Sun than we are at any other time of year.
  2.  
     

    Ole Nielsen - Aphelion and 4 July

    my.opera.com/nielsol/blog/.../aphelion-and-4-jul...En caché - Traducir esta página
    3 Jul 2011 – For the time being the fourth of July is the “typical day” of aphelion, that is with an occasional exception, due to leap years, every now and then, ...
  3.  
     

    NIGHT SKY~APHELION DAY

    www.souledout.org/.../aphelionday/aphelionday....En caché - Similares - Traducir esta página
    In 2012 the exact time of aphelion is July 4 at 9:00pm PDT (04:00 UT July 5). On July 4 we are 94.5 million miles away from the Sun, which is 3 million miles ...
  4.  
     

    Earth's Seasons — Naval Oceanography Portal

    www.usno.navy.mil › ... › Data ServicesEn caché - Traducir esta página
    d h d h m d h m 2000 2000 Perihelion Jan 3 05 Equinoxes Mar 20 07 35 Sept 22 17 28 Aphelion July 4 00 Solstices June 21 01 48 Dec 21 ...
  5.  
     

    Apsis - Wikipedia, the free encyclopedia

    en.wikipedia.org/wiki/ApsisEn caché - Similares - Traducir esta página
    For the literary journal, see Perigee: Publication for the Arts. For .... Likewise, the annual aphelion currently occurs in early July, about 14 days after the June ...
  6.  
     

    Aphelion Day - NASA Science

    science.nasa.gov › ... › 2000En caché - Similares - Traducir esta página
    6 Apr 2011 – This year aphelion falls on Independence Day holiday in the U.S." Above: After sunset on the 4th of July, a slender crescent moon seen low in ...
  7.  
     

    Aphelion Away! - NASA Science

    science.nasa.gov › ... › 2001En caché - Similares - Traducir esta página
    20 Sep 2011 – On the 4th of July, Earth will lie at its greatest distance from the Sun -- an annual event astronomers call "aphelion." But don't expect any ...
  8.  
     

    APOD: 2009 July 3 - Perihelion and Aphelion

    apod.nasa.gov/apod/ap090703.htmlEn caché - Similares - Traducir esta página
    3 Jul 2009 – Explanation: This year Aphelion, the point in Earth's elliptical orbit when it is farthest from the Sun, occurs tomorrow, July 4th. Of course, that ...
     
  9.  
     

    Aphelion 2011 « Dark Sky Diary

    darkskydiary.wordpress.com/.../aphelion-2011/En caché - Traducir esta página
    4 Jul 2011 – At 1600 BST (1500 GMT) on 4 July 2011 the Earth will be at aphelion, its furthest from the Sun this year. If that sounds confusing to you, and has ...
  10.  
     

    Earth farthest from sun for 2012 on July 4 | Tonight | EarthSky

    earthsky.org/.../earth-farthest-from-sun-for-year-...En caché - Traducir esta página
    On July 4, 2012, our planet Earth reaches aphelion - its most distant point from the sun for the year. We're 152092425 kilometers away at aphelion 2012.
 
 

Resposta  Mensagem 5 de 97 no assunto 
De: BARILOCHENSE6999 Enviado: 27/08/2012 00:02
Image

Blackwell coat of arms - the underworld dog - Anubis - Aquarius symbol design

K - 9 letter number 11 - 9-11 and Sirius code - Jacob's ladder


Image

Image

http://en.wikipedia.org/wiki/Police_dog

A police dog, often referred to as a "K-9" (which is a homophone of canine) in some areas, is a dog that is trained specifically to assist police and other law-enforcement personnel in their work. The most commonly used breed is the German Shepherd, although now Belgian Malinois are also fairly popular dogs to use. In many jurisdictions the intentional injuring or killing of a police dog is a felony,[1] subjecting the perpetrator to harsher penalties than those in the statutes embodied in local animal cruelty laws,[2] just as an assault on a human police officer is often a more serious offense than the same assault on a non-officer. A growing number of law-enforcement organizations outfit dogs with ballistic vests,[3][4] and some make the dogs sworn officers, with their own police badges and IDs.[1][5][6][7] Furthermore, a police dog killed in the line of duty is often given a full police funeral.


http://www.bibliotecapleyades.net/universo/siriusmystery/siriusmystery03.htm

Resposta  Mensagem 6 de 97 no assunto 
De: BARILOCHENSE6999 Enviado: 27/08/2012 00:23
Image

Serendipity, how about the last supper ?

Resposta  Mensagem 7 de 97 no assunto 
De: BARILOCHENSE6999 Enviado: 27/08/2012 16:28
 
Image


Rennes le Chateau floor and the Merovingian Abbey of St Germain keys of the rhombic dodecahedron beehive construction as Gods singular supersymmetry particle in micro and microcosmos, understanding the reptilian geometric rhombic skin arcehtype key and the draco/dragon galactic center chaos fire of death and regeneration which opens the underworld gates.
The golden bees of the Merovingians used by Napoleon symbolized the new golden age brought by the beehive galactic formation towards the regualar octagonal Knight Templar cross, the Sol-o-mon temple concept.

Sol = Sun
O= 15 =1111
mon=1singularity mon-key

Mon-a Lisa-rd reptilian rhombic skin
Mon-key
A-lpha/Aquarius
Lisa-rd


--------------------------------------


Diamagnetic - Magnetic Day

Lets add some new concepts to the last posts so you can understand the superconductivity geometric keys of God's microcosmos particle which in effect it's geometry seems to equate the microcosmos galactic hypercube process of singularity.
Note that Higgs mechanism is based on superconductivity fluxes arranged in 2 D hexagonal lattice and make your bet that in a 3D rhombic dodecahedron space filling net.
Lets remeber the superconductivity diamagnetic key related with the rhombic lattice such as birefrigerent calcite crystals or bismuth used by UFOS for antigravity technology.
Superconductivity - ELF - Titan Saturn frozen moon singularity superconductivity fabric keys of the Titan Olympic God's return through Phaeton's chaotic fire charriot.


http://en.wikipedia.org/wiki/Higgs_mechanism

Higgs mechanism

Landau model

The Higgs mechanism is a type of superconductivity which occurs in the vacuum. It occurs when all of space is filled with a sea of particles which are charged, or, in field language, when a charged field has a nonzero vacuum expectation value. Interaction with the quantum fluid filling the space prevents certain forces from propagating over long distances (as it does in a superconducting medium; e.g., in the Ginzburg–Landau theory).
A superconductor expels all magnetic fields from its interior, a phenomenon known as the Meissner effect. This was mysterious for a long time, because it implies that electromagnetic forces somehow become short-range inside the superconductor. Contrast this with the behavior of an ordinary metal. In a metal, the conductivity shields electric fields by rearranging charges on the surface until the total field cancels in the interior. But magnetic fields can penetrate to any distance, and if a magnetic monopole (an isolated magnetic pole) is surrounded by a metal the field can escape without collimating into a string. In a superconductor, however, electric charges move with no dissipation, and this allows for permanent surface currents, not just surface charges. When magnetic fields are introduced at the boundary of a superconductor, they produce surface currents which exactly neutralize them. The Meissner effect is due to currents in a thin surface layer, whose thickness, the London penetration depth, can be calculated from a simple model (the Ginzburg–Landau theory).

http://en.wikipedia.org/wiki/Ginzburg%E ... dau_theory

The most important finding from Ginzburg–Landau theory was made by Alexei Abrikosov in 1957. In a type-II superconductor in a high magnetic field – the field penetrates in quantized tubes of flux, which are most commonly arranged in a hexagonal lattice.
The exponential decay of the magnetic field is equivalent with the Higgs mechanism in high-energy physics.

Landau–Ginzburg theories in particle physics

In particle physics, any quantum field theory with a unique classical vacuum state and a potential energy with a degenerate critical point is called a Landau–Ginzburg theory. The generalization to N=(2,2) supersymmetric theories in 2 spacetime dimensions was proposed by Cumrun Vafa and Nicholas Warner in the November 1988 article Catastrophes and the Classification of Conformal Theories, in this generalization one imposes that the superpotential possess a degenerate critical point. The same month, together with Brian Greene they argued that these theories are related by a renormalization group flow to sigma models on Calabi–Yau manifolds in the paper Calabi–Yau Manifolds and Renormalization Group Flows. In his 1993 paper Phases of N=2 theories in two-dimensions, Edward Witten argued that Landau–Ginzburg theories and sigma models on Calabi–Yau manifolds are different phases of the same theory.



Image


4 July Sirius dependence

The Dog Days Sirius heliacal rising starts in Cancer/July as Sirius/Isis rotates clockwise in the opposite direction of our Sun and Orion/Osiris - remember the buTTon/boTTom under the middle of the Arch-i-medes Arch TT code woman clockwise - man counterclockwise.
When 9 and 6 spirals crash in the galactic center the energetic gamma ray beams folds space creating the wormohole.The Christ conception, the galactic sexual union of Osiris obelisk phallus and Isis vesica piscis/vagina.
As in economy chaos brings opportunities in this case brings the return of the immortal Titan Gods of the underworld.
2012 London/Zion olympic games and Phaeton chaotic charriot symbolism.
Ambrosia - Amber- rose the food of the Gods, electric amber plus the Rosae crucis, last cycle of Venus/Isis retrograde 9 spiral path over the bull horns.

Man-a
Man - Alpha/Aquarius

H - I- RAM ABI-F
H= 8 the hypercube
I = 9 galactic center clockwise/Isis/Venus
Ram - Aries
Abi = Abyss
F = 6 counterclockwise/Osiris/Saturn/Sun

RAM-SES - Aries 6

G-HOST
G= 7 Aries - host
 


Primeira  Anterior  2 a 7 de 97  Seguinte   Última 
Assunto anterior  Assunto seguinte
 
©2025 - Gabitos - Todos os direitos reservados