|
|
MATEMATICAS: ARCHIMEDES (CIRCULO, ELIPSE, PARABOLA E HIPERBOLA)
Triar un altre plafó de missatges |
|
|
The cone hat and time.C - ONE 3 Trinity -mon-key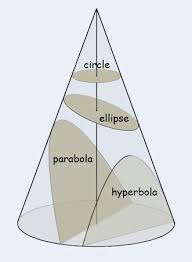 Conic sections - orbits - space and time Conic sections - orbits - space and time Mic-key 8 pointed star - golden age Mic-key 8 pointed star - golden age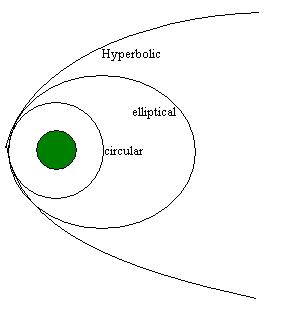 The lines traced out by orbits dominated by the gravity of a central source are conic sections: the shapes of the curves of intersection between a plane and a cone. Parabolic (1) and hyperbolic (3) orbits are escape orbits, whereas elliptical and circular orbits (2) are captive. The lines traced out by orbits dominated by the gravity of a central source are conic sections: the shapes of the curves of intersection between a plane and a cone. Parabolic (1) and hyperbolic (3) orbits are escape orbits, whereas elliptical and circular orbits (2) are captive. Squint eyed Mon-k-ey /12 Mon-keys with Broad Pit and Madelaine StowedBald cosmic egg head The orbital eccentricity of an astronomical object is a parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptical orbit, 1 is a parabolic escape orbit, and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the galaxy. Squint eyed Mon-k-ey /12 Mon-keys with Broad Pit and Madelaine StowedBald cosmic egg head The orbital eccentricity of an astronomical object is a parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptical orbit, 1 is a parabolic escape orbit, and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the galaxy.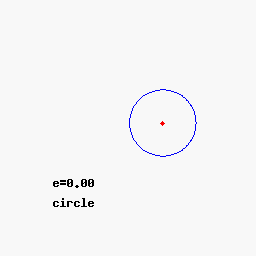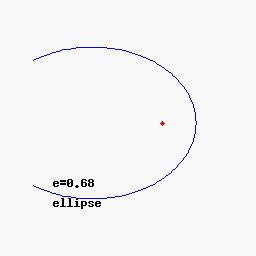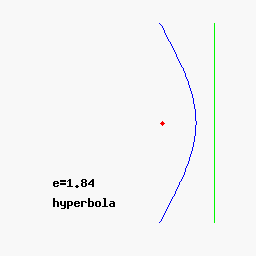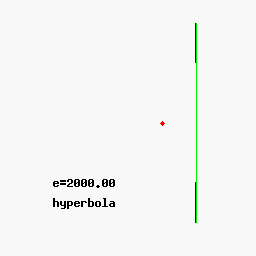 Mercury has the greatest orbital eccentricity of any planet in the Solar System (e=0.2056). Before 2006, Pluto was considered to be the planet with the most eccentric orbit (e=0.248). The Moon's value is 0.0549. Mercury has the greatest orbital eccentricity of any planet in the Solar System (e=0.2056). Before 2006, Pluto was considered to be the planet with the most eccentric orbit (e=0.248). The Moon's value is 0.0549.  Speedy Quicksilver Mercury messenger of the Gods, more speed more eccentricity - escaping orbits = chaos Speedy Quicksilver Mercury messenger of the Gods, more speed more eccentricity - escaping orbits = chaos This is the hardest case and includes the serpentine curve as one of the subcases. The third class wasxy=ax³+bx²+cx+d,(4)which is called Newton's diverging parabolas. Newton's 66th curve was the trident of Newton. Newton's classification of cubics was criticized by Euler because it lacked generality. This is the hardest case and includes the serpentine curve as one of the subcases. The third class wasxy=ax³+bx²+cx+d,(4)which is called Newton's diverging parabolas. Newton's 66th curve was the trident of Newton. Newton's classification of cubics was criticized by Euler because it lacked generality.   Horus eye progression Horus eye progression  Archimedes' dissection of a parabolic segment into infinitely many triangles.Dissection of the parabolic segmentThe main idea of the proof is the dissection of the parabolic segment into infinitely many triangles, as shown in the figure to the right. Each of these triangles is inscribed in its own parabolic segment in the same way that the blue triangle is inscribed in the large segment.[edit]Areas of the trianglesIn propositions eighteen through twenty-one, Archimedes proves that the area of each green triangle is one eighth of the area of the blue triangle. From a modern point of view, this is because the green triangle has half the width and a fourth of the height:[1]By extension, each of the yellow triangles has one eighth the area of a green triangle, each of the red triangles has one eighth the area of a yellow triangle, and so on. Using the method of exhaustion, it follows that the total area of the parabolic segment is given by Archimedes' dissection of a parabolic segment into infinitely many triangles.Dissection of the parabolic segmentThe main idea of the proof is the dissection of the parabolic segment into infinitely many triangles, as shown in the figure to the right. Each of these triangles is inscribed in its own parabolic segment in the same way that the blue triangle is inscribed in the large segment.[edit]Areas of the trianglesIn propositions eighteen through twenty-one, Archimedes proves that the area of each green triangle is one eighth of the area of the blue triangle. From a modern point of view, this is because the green triangle has half the width and a fourth of the height:[1]By extension, each of the yellow triangles has one eighth the area of a green triangle, each of the red triangles has one eighth the area of a yellow triangle, and so on. Using the method of exhaustion, it follows that the total area of the parabolic segment is given by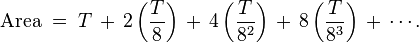 Here T represents the area of the large blue triangle, the second term represents the total area of the two green triangles, the third term represents the total area of the four yellow triangles, and so forth. This simplifies to give Here T represents the area of the large blue triangle, the second term represents the total area of the two green triangles, the third term represents the total area of the four yellow triangles, and so forth. This simplifies to give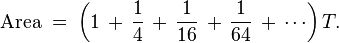  Archimedes' proof that 1/4 + 1/16 + 1/64 + ... = 1/3Sum of the seriesTo complete the proof, Archimedes shows that Archimedes' proof that 1/4 + 1/16 + 1/64 + ... = 1/3Sum of the seriesTo complete the proof, Archimedes shows that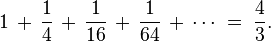 The formula above is a geometric series—each successive term is one fourth of the previous term. In modern mathematics, that formula is a special case of the sum formula for a geometric series.Archimedes evaluates the sum using an entirely geometric method,[2] illustrated in the picture to the right. This picture shows a unit square which has been dissected into an infinity of smaller squares. Each successive purple square has one fourth the area of the previous square, with the total purple area being the sum The formula above is a geometric series—each successive term is one fourth of the previous term. In modern mathematics, that formula is a special case of the sum formula for a geometric series.Archimedes evaluates the sum using an entirely geometric method,[2] illustrated in the picture to the right. This picture shows a unit square which has been dissected into an infinity of smaller squares. Each successive purple square has one fourth the area of the previous square, with the total purple area being the sum However, the purple squares are congruent to either set of yellow squares, and so cover 1/3 of the area of the unit square. It follows that the series above sums to 4/3.4/3 = 8/6 Octagon order/Hexagon chaos = 1.3333... However, the purple squares are congruent to either set of yellow squares, and so cover 1/3 of the area of the unit square. It follows that the series above sums to 4/3.4/3 = 8/6 Octagon order/Hexagon chaos = 1.3333...
_________________
E.T.A.E
|
|
|
|
|
3,4,5 Khefren 53,4 - Jesus 33 - 53,4/33=1,618
5,12,13 triangle doubled = octagon rectangle
From 6 hexagon/chaos to 8 octagon/order
Ordo ab Chao 33 |
|
|
|
|
| |
|
|
©2025 - Gabitos - Tots els drets reservats | |
|
|

