|
|
Cerca de 480.000 resultados

es.dreamstime.com
Código digital binario
1300 × 1390 - 786k - jpg |

cmapspublic2.ihmc.us
-de-tecnologia-digital-gl.
1200 × 927 - 246k - jpg |

canstockphoto.es
verde, digital, binario
450 × 320 - 43k - jpg |

es.dreamstime.com
Ciudad digital binaria, fondo
1300 × 960 - 200k - jpg |

es.dreamstime.com
Extracto del indicador digital
1300 × 957 - 313k - jpg |

es.dreamstime.com
Tecnología digital originada
1300 × 1009 - 404k - jpg |

canstockphoto.es
3D, mundo, mapa, binario,
450 × 351 - 53k - jpg |

blog.fundacionmontemad...
Código binario
281 × 400 - 216k - png |

portafolio-09.blogspot...
ocho digitos binarios se
303 × 227 - 24k - jpeg |

ciberescuela103vargasd...
en tecnología digital y
1200 × 900 - 292k - jpg |

curiosidades.batanga.com
Electronica-sistema-binario-y-
657 × 768 - 83k - jpg |

canstockphoto.es
digital, binario, código,
450 × 470 - 67k - jpg |

tecnologiaeinformatica...
sistema binario
199 × 197 - 12k - jpg |

es.123rf.com
binario tecnología digital
1350 × 954 - 170k - jpg |

es.dreamstime.com
Ciudad abstracta binaria
1300 × 1065 - 140k - jpg |

curiosidades.batanga.com
Electronica-sistema-binario-y-
630 × 473 - 50k - jpg |

ensvrinconlealnuevedos...
Cronómetro: El sistema binario
1024 × 1024 - 419k - png |

tecnologia-crito-rey.w...
El sistema binario, en
640 × 480 - 518k - jpg |

es.clipart.me
de la tecnología digital
379 × 269 - 19k - jpg |

es.vectorhq.com
de la tecnología digital
450 × 318 - 45k - jpg |
|
|
|
|
|
RELACION DE LOS SISTEMAS DIGITALES, CON EL SISTEMA BINARIO=2, OCTAL=8 Y HEXADECIMAL=16.
|
|
|
|
|
|
| Reply |
Message 8 of 8 on the subject |
|
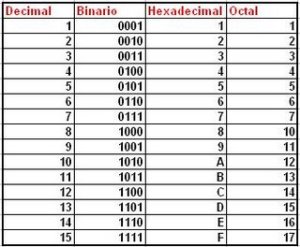
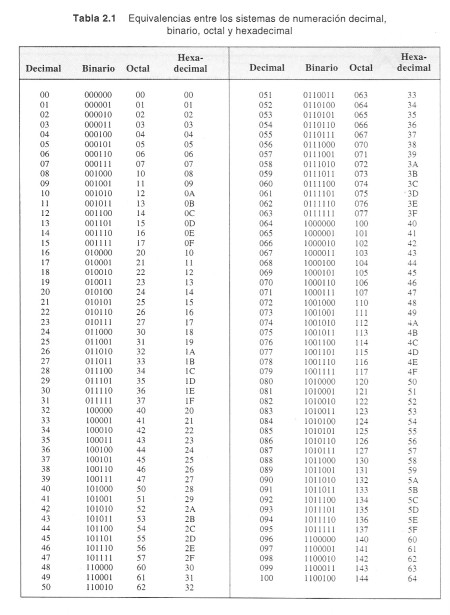
Los sistemas de numeración son conjuntos de dígitos usados para representar cantidades, así se tienen los sistemas de numeración decimal, binario, octal, hexadecimal, romano, etc. Los cuatro primeros se caracterizan por tener una base (número de dígitos diferentes: diez, dos, ocho, dieciseis respectivamente) mientras que el sistema romano no posee base y resulta más complicado su manejo tanto con números, así como en las operaciones básicas.
Los sistemas de numeración que poseen una base tienen la característica de cumplir con la notación posicional, es decir, la posición de cada número le da un valor o peso, así el primer dígito de derecha a izquierda después del punto decimal, tiene un valor igual a b veces el valor del dígito, y así el dígito tiene en la posición n un valor igual a: (bn) * A
donde:
b = valor de la base del sistema
n = número del dígito o posición del mismo
A = dígito.
El sistema de numeración más simple que usa la notación posicional es el sistema de numeración binario. Este sistema, como su nombre lo indica, usa solamente dos dígitos (0,1). Por su simplicidad y por poseer únicamente dos dígitos diferentes, el sistema de numeración binario se usa en computación para el manejo de datos e información.
A la representación de un dígito binario se le llama bit y al conjunto de 8 bits se le llama byte, así por ejemplo: 110 contiene 3 bits, 1001 contiene 4 y 1 contiene 1 bit.
Como el sistema binario usa la notación posicional entonces el valor de cada dígito depende de la posición que tiene en el número, así por ejemplo el número 110101b es:
1*(20) + 0*(21) + 1*(22) + 0*(23) + 1*(24) + 1*(25) = 1 + 4 + 16 + 32 = 53d
El sistema de numeración octal es también muy usado en la computación por tener una base que es potencia exacta de 2 o de la numeración binaria. Esta característica hace que la conversión a binario o viceversa sea bastante simple. El sistema octal usa 8 dígitos (0,1,2,3,4,5,6,7) y tienen el mismo valor que en el sistema de numeración decimal. Como el sistema de numeración octal usa la notación posicional entonces para el número 3452.32q tenemos:
2*(80) + 5*(81) + 4*(82) + 3*(83) + 3*(8-1) + 2*(8-2) = 2 + 40 + 4*64 + 64 + 3*512 + 3*0.125 + 2*0.015625 = 2 + 40 + 256 + 1536 + 0.375 + 0.03125 = 1834 + 40625d entonces, 3452.32q = 1834.40625d
El sistema de numeración decimal es el más usado, tiene como base el número 10, o sea que posee 10 dígitos diferentes (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). El sistema de numeración decimal fué desarrollado por los hindúes, posteriormente lo introducen los árabes en Europa, donde recibe el nombre de sistema de numeración decimal o arábigo. Si se aplica la notación posicional al sistema de numeración decimal entonces el dígito número n tiene el valor: (10n)* A
Este valor es positivo y es mayor o igual que uno si el dígito se localiza a la izquierda del punto decimal y depende del dígito A, en cambio el valor es menor que uno si el dígito se localiza a la derecha del punto decimal.
Un gran problema con el sistema binario es la verbosidad. El sistema de numeración hexadecimal, o sea de base 16, resuelve este problema (es común abreviar hexadecimal como hex aunque hex significa base seis y no base dieciseis). El sistema hexadecimal es compacto y nos proporciona un mecanismo sencillo de conversión hacia el formato binario, debido a ésto, la mayoría del equipo de cómputo actual utiliza el sistema numérico hexadecimal. Como la base del sistema hexadecimal es 16, cada dígito a la izquierda del punto hexadecimal representa tantas veces un valor sucesivo potencia de 16, por ejemplo, el número 123416 es igual a:
1*163 + 2*162 + 3*161 + 4*160
lo que da como resultado:
4096 + 512 + 48 + 4 = 466010
Cada dígito hexadecimal puede representar uno de dieciseis valores entre 0 y 1510. Como sólo tenemos diez dígitos decimales, necesitamos inventar seis dígitos adicionales para representar los valores entre 1010 y 1510. En lugar de crear nuevos símbolos para estos dígitos, utilizamos las letras A a la F.
|
| Reply |
Message 7 of 7 on the subject |
|
|
|
|
|
|
|
|
|
|


“XP” or “Chi-Rho” Sign of Constantine

“XP” Sign of Constantine to match Precession of the Equinoxes in St Peter’s Square, and the increasing quantum entanglement of the Timelines of 2 solar systems (represented at each side of the obelisk) intended to MERGE AS ONE at the center obelisk
|
|
|
|
|





System Failure, time for Reset; the inevitable “SOFTWARE EXPIRE” within the Timelines quantum programming
|
|
|
|
|
EL HIPERCUBO, LA CUARTA DIMENSION, EL TIEMPO, LA LEY DE LA RELATIVIDAD DE EINSTEIN Y SU NEXO CON MARCOS 15:33
33. Marcos 15:33: Cuando vino la hora SEXTa, hubo tinieblas sobre toda la tierra hasta la hora novena. (CLAVE MERCURIO-ORION-ISHTAR GATE)

Decimal --- Binario --- Cuaternario
00 -------- 0000 ------ 00
01 -------- 0001 ------ 01
02 -------- 0010 ------ 02
03 -------- 0011 ------ 03
04 -------- 0100 ------ 10
05 -------- 0101 ------ 11
06 -------- 0110 ------ 12
07 -------- 0111 ------ 13
08 -------- 1000 ------ 20
09 -------- 1001 ------ 21
10 -------- 1010 ------ 22
11 -------- 1011 ------ 23
12 -------- 1100 ------ 30
13 -------- 1101 ------ 31
14 -------- 1110 ------ 32
15 -------- 1111 ------ 33
Las Triadas "que nos elevan" como acordes (11, 111, 1111) a través de sus ejes o colúmnas pitagóricas. Los puntos de corte de dos dimensiones.
Aquí el el 3, 7 y 15 decimal, o 3, 13, 33 cuaternario. Puntos, entiendo, de la singularidad en tres planos diferentes. O como fusión de contrarios.
3 veces 3 que nos llevan hasta la eclosión del huevo -singularidad fecundativa-.

3 veces 3 como el PLATO (PI-LATO) de Giza. 3 pirámides grandes, 3 pirámides pequeñas (6) y 9 (3+3+3) en total. 369.
http://www.burbuja.info/inmobiliaria/conspiraciones/297306-hilo-oficial-indigomerovingio-148.html
 |
Click para ampliar |
  Lo que me lleva a relacionar esto del 3 veces 3 con los armónicos solfeggio y sus puntos de corte o frecuencias doradas, donde el "dragón se eleva" Lo que me lleva a relacionar esto del 3 veces 3 con los armónicos solfeggio y sus puntos de corte o frecuencias doradas, donde el "dragón se eleva"
 |
Click para ampliar |
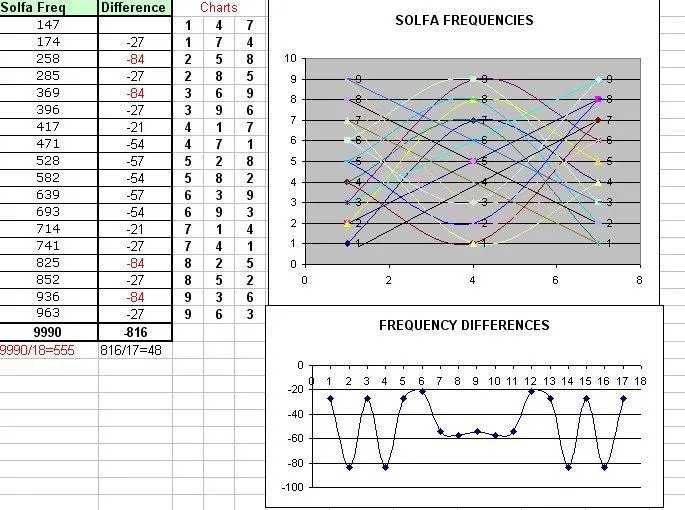 Bettle-Juice, Beetle-Juice, Beetle-Juice.Veo ademas que la suma reducida es 3-6-9. Bettle-Juice, Beetle-Juice, Beetle-Juice.Veo ademas que la suma reducida es 3-6-9.
 |
Click para ampliar |
 3 veces 3. 3 veces 3.
Viene de digitalización de primera semana de curso:
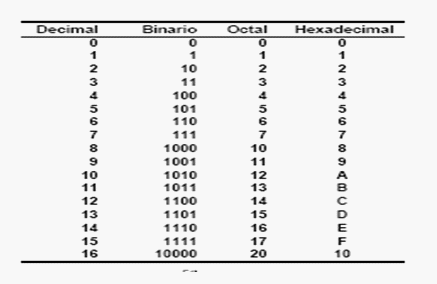
El concepto, que no es nuevo, es que los dieciséis primeros números decimales se pueden mostrar en un nibble binario (medio Byte) resultando 1111 como indicaba IM al representar las coordenadas de los vértices del cubo 4D...
Ahora viene el nuevo apunte...
Que pasa si mostramos esos mismo número decimales en un sistema en base cuatro o cuaternario:
Decimal --- Binario --- Cuaternario
00 -------- 0000 ------ 00
01 -------- 0001 ------ 01
02 -------- 0010 ------ 02
03 -------- 0011 ------ 03
04 -------- 0100 ------ 10
05 -------- 0101 ------ 11
06 -------- 0110 ------ 12
07 -------- 0111 ------ 13
08 -------- 1000 ------ 20
09 -------- 1001 ------ 21
10 -------- 1010 ------ 22
11 -------- 1011 ------ 23
12 -------- 1100 ------ 30
13 -------- 1101 ------ 31
14 -------- 1110 ------ 32
15 -------- 1111 ------ 33
Inquietante... 
¿Esta letra en base cuatro como se podría representar físicamente? Considero que lo mas adecuado sería un tetraedro regular (formado por 4 triángulos equiláteros), el primero de los sólidos platónicos. Donde cada uno de sus cuatro vértices se encuentran a distancias simétricas entre ellas.
Como para representar el 15 decimal (el 33 en base 4) se necesitan dos dígitos en cuaternario, la forma física de integrar ambas letras sería mediante dos tetraedros unidos en que su vórtices continuaran de forma simétrica.
Resumiendo se puede decir, que un hipercubo es lo mismo que lo que se suele representar como Merkaba
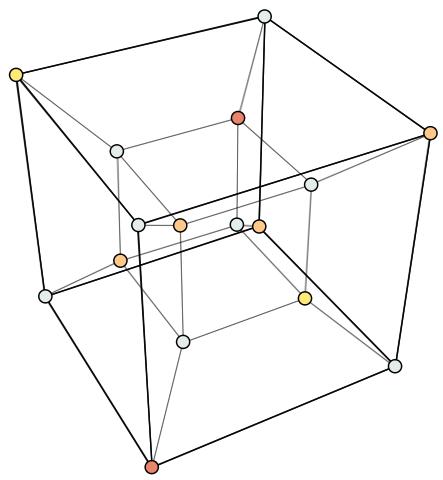


...
..
.
Y que este simbolismo:

Es igual a este:

O al menos que debe representar un concepto muy similar...
|
|
|
|
|
EL SISTEMA HEXADECIMAL DE LAS COMPUTADORAS TIENE FUERTE CONNOTACION CON EL "AGUJERO DE GUSANO"
Tabla de conversión entre decimal, binario, hexadecimal y octal[editar]
| Decimal | Binario | Hexadecimal | octal |
| 0 |
00000 |
0 |
0 |
| 1 |
00001 |
1 |
1 |
| 2 |
00010 |
2 |
2 |
| 3 |
00011 |
3 |
3 |
| 4 |
00100 |
4 |
4 |
| 5 |
00101 |
5 |
5 |
| 6 |
00110 |
6 |
6 |
| 7 |
00111 |
7 |
7 |
| 8 |
01000 |
8 |
10 |
| 9 |
01001 |
9 |
11 |
| 10 |
01010 |
A |
12 |
| 11 |
01011 |
B |
13 |
| 12 |
01100 |
C |
14 |
| 13 |
01101 |
D |
15 |
| 14 |
01110 |
E |
16 |
| 15 |
01111 |
F |
17 |
| 16 |
10000 |
10 |
20 |
| 17 |
10001 |
11 |
21 |
| 18 |
10010 |
12 |
22 |
| 19 |
10011 |
13 |
23 |
| 20 |
10100 |
14 |
24 |
| 21 |
10101 |
15 |
25 |
| 22 |
10110 |
16 |
26 |
| 23 |
10111 |
17 |
27 |
| 24 |
11000 |
18 |
30 |
| 25 |
11001 |
19 |
31 |
| 26 |
11010 |
1A |
32 |
| 27 |
11011 |
1B |
33 |
| 28 |
11100 |
1C |
34 |
| 29 |
11101 |
1D |
35 |
| 30 |
11110 |
1E |
36 |
| 31 |
11111 |
1F |
37 |
| 32 |
100000 |
20 |
40 |
| 33 |
100001 |
21 |
41 |
|
|
|
|
|
Sistema hexadecimal
De Wikipedia, la enciclopedia libre
El sistema hexadecimal (a veces abreviado como Hex, no confundir con sistema sexagesimal) es el sistema de numeración posicional que tiene como base el 16. Su uso actual está muy vinculado a la informática y ciencias de la computación, pues los computadores suelen utilizar el byte u octeto como unidad básica de memoria; y, debido a que un byte representa 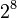 valores posibles, y esto puede representarse como valores posibles, y esto puede representarse como 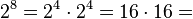  , que equivale al número en base 16 , que equivale al número en base 16 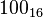 , dos dígitos hexadecimales corresponden exactamente a un byte. , dos dígitos hexadecimales corresponden exactamente a un byte.
En principio, dado que el sistema usual de numeración es de base decimal y, por ello, sólo se dispone de diez dígitos, se adoptó la convención de usar las seis primeras letras del alfabeto latino para suplir los dígitos que nos faltan. El conjunto de símbolos sería, por tanto, el siguiente:

Se debe notar que A = 10, B = 11, C = 12, D = 13, E = 14 y F = 15. En ocasiones se emplean letras minúsculas en lugar de mayúsculas. Como en cualquier sistema de numeración posicional, el valor numérico de cada dígito es alterado dependiendo de su posición en la cadena de dígitos, quedando multiplicado por una cierta potencia de la base del sistema, que en este caso es 16. Por ejemplo: 3E0A16 = 3×163 + E×162 + 0×161 + A×160 = 3×4096 + 14×256 + 0×16 + 10×1 = 15882.
El sistema hexadecimal actual fue introducido en el ámbito de la computación por primera vez por IBM en 1963. Una representación anterior, con 0–9 y u–z, fue usada en 1956 por la computadora Bendix G-15.
Tabla de conversión entre decimal, binario, octal y hexadecimal[editar]
| |
|
|
|
|
|
|
|
|
|
|
|
| |
0hex |
= |
0dec |
= |
0oct |
|
0 |
0 |
0 |
0 |
|
| |
1hex |
= |
1dec |
= |
1oct |
|
0 |
0 |
0 |
1 |
|
| |
2hex |
= |
2dec |
= |
2oct |
|
0 |
0 |
1 |
0 |
|
| |
3hex |
= |
3dec |
= |
3oct |
|
0 |
0 |
1 |
1 |
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
4hex |
= |
4dec |
= |
4oct |
|
0 |
1 |
0 |
0 |
|
| |
5hex |
= |
5dec |
= |
5oct |
|
0 |
1 |
0 |
1 |
|
| |
6hex |
= |
6dec |
= |
6oct |
|
0 |
1 |
1 |
0 |
|
| |
7hex |
= |
7dec |
= |
7oct |
|
0 |
1 |
1 |
1 |
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
8hex |
= |
8dec |
= |
10oct |
|
1 |
0 |
0 |
0 |
|
| |
9hex |
= |
9dec |
= |
11oct |
|
1 |
0 |
0 |
1 |
|
| |
Ahex |
= |
10dec |
= |
12oct |
|
1 |
0 |
1 |
0 |
|
| |
Bhex |
= |
11dec |
= |
13oct |
|
1 |
0 |
1 |
1 |
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
Chex |
= |
12dec |
= |
14oct |
|
1 |
1 |
0 |
0 |
|
| |
Dhex |
= |
13dec |
= |
15oct |
|
1 |
1 |
0 |
1 |
|
| |
Ehex |
= |
14dec |
= |
16oct |
|
1 |
1 |
1 |
0 |
|
| |
Fhex |
= |
15dec |
= |
17oct |
|
1 |
1 |
1 |
1 |
|
| |
|
|
|
|
|
|
|
|
|
|
|
Como el único factor primo de 16 es 2, todas las fracciones que no tengan una potencia de 2 en el denominador, tendrán un desarrollo hexadecimal periódico.
| Fracción | Hexadecimal | Resultado en hexadecimal |
| 1/2 |
1/2 |
0,8 |
| 1/3 |
1/3 |
0,5 periodo |
| 1/4 |
1/4 |
0,4 |
| 1/6 |
1/6 |
0,2A periodo |
| 1/7 |
1/7 |
0,249 periodo |
| 1/8 |
1/8 |
0,2 |
| 1/9 |
1/9 |
0,1C7 periodo |
| 1/10 |
1/A |
0,19 periodo |
| 1/11 |
1/B |
0,1745D periodo |
| 1/12 |
1/C |
0,15 periodo |
| 1/13 |
1/D |
0,13B periodo |
| 1/14 |
1/E |
0,1249 periodo |
| 1/15 |
1/F |
0,1 periodo |
| 1/16 |
1/10 |
0,1 |
Existe un sistema para convertir números fraccionarios a hexadecimal de una forma más mecánica. Se trata de convertir la parte entera con el procedimiento habitual y convertir la parte decimal aplicando sucesivas multiplicaciones por 16 hasta convertir el resultado en un número entero.
Por ejemplo: 0,06640625 en base decimal.
Multiplicado por 16: 1,0625, el primer decimal será 1. Volvemos a multiplicar por 16 la parte decimal del anterior resultado: 1. Por lo tanto el siguiente decimal será un 1.Resultado: 0,11 en base hexadecimal. Como el último resultado se trata de un entero, hemos acabado la conversión.
Hay ocasiones en las que no llegamos nunca a obtener un número entero, en ese caso tendremos un desarrollo hexadecimal periódico.
|
|
|
|
|
MATRIX="TODOS LOS SISTEMAS DE COMPUTADORAS A NIVEL MUNDIAL ESTAN DISEÑADOS CON EL PATRON 2,8 Y 16 EN UN CONTEXTO A VENUS"
SABEMOS QUE EL CICLO SIDEREO DE VENUS ES IGUAL A 225. TENEMOS QUE 8 POR 225 ES IGUAL A 1800 Y QUE INCLUSO 16*225=3600. OSEA QUE EN ESTE MARCO TENEMOS QUE EL SISTEMA SEXAGECIMAL TIENE ORIGEN EN LOS CICLOS DE VENUS. LO CURIOSO ES QUE TODO EL SISTEMA DIGITAL TIENE RELACION INSISTO, CON DICHOS NUMEROS.
 |
|
8 * 225 = 1800
|
 |
|
16 * 225 = 3600
|
 



EL SISTEMA HEXADECIMAL DE LAS COMPUTADORAS TIENE FUERTE CONNOTACION CON EL "AGUJERO DE GUSANO"
Tabla de conversión entre decimal, binario, hexadecimal y octal[editar]
| Decimal | Binario | Hexadecimal | octal |
| 0 |
00000 |
0 |
0 |
| 1 |
00001 |
1 |
1 |
| 2 |
00010 |
2 |
2 |
| 3 |
00011 |
3 |
3 |
| 4 |
00100 |
4 |
4 |
| 5 |
00101 |
5 |
5 |
| 6 |
00110 |
6 |
6 |
| 7 |
00111 |
7 |
7 |
| 8 |
01000 |
8 |
10 |
| 9 |
01001 |
9 |
11 |
| 10 |
01010 |
A |
12 |
| 11 |
01011 |
B |
13 |
| 12 |
01100 |
C |
14 |
| 13 |
01101 |
D |
15 |
| 14 |
01110 |
E |
16 |
| 15 |
01111 |
F |
17 |
| 16 |
10000 |
10 |
20 |
| 17 |
10001 |
11 |
21 |
| 18 |
10010 |
12 |
22 |
| 19 |
10011 |
13 |
23 |
| 20 |
10100 |
14 |
24 |
| 21 |
10101 |
15 |
25 |
| 22 |
10110 |
16 |
26 |
| 23 |
10111 |
17 |
27 |
| 24 |
11000 |
18 |
30 |
| 25 |
11001 |
19 |
31 |
| 26 |
11010 |
1A |
32 |
| 27 |
11011 |
1B |
33 |
| 28 |
11100 |
1C |
34 |
| 29 |
11101 |
1D |
35 |
| 30 |
11110 |
1E |
36 |
| 31 |
11111 |
1F |
37 |
| 32 |
100000 |
20 |
40 |
| 33 |
100001 |
21 |
41 |
Sistema hexadecimal
De Wikipedia, la enciclopedia libre
El sistema hexadecimal (a veces abreviado como Hex, no confundir con sistema sexagesimal) es el sistema de numeración posicional que tiene como base el 16. Su uso actual está muy vinculado a la informática y ciencias de la computación, pues los computadores suelen utilizar el byte u octeto como unidad básica de memoria; y, debido a que un byte representa 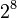 valores posibles, y esto puede representarse como valores posibles, y esto puede representarse como 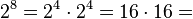  , que equivale al número en base 16 , que equivale al número en base 16 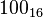 , dos dígitos hexadecimales corresponden exactamente a un byte. , dos dígitos hexadecimales corresponden exactamente a un byte.
En principio, dado que el sistema usual de numeración es de base decimal y, por ello, sólo se dispone de diez dígitos, se adoptó la convención de usar las seis primeras letras del alfabeto latino para suplir los dígitos que nos faltan. El conjunto de símbolos sería, por tanto, el siguiente:

Se debe notar que A = 10, B = 11, C = 12, D = 13, E = 14 y F = 15. En ocasiones se emplean letras minúsculas en lugar de mayúsculas. Como en cualquier sistema de numeración posicional, el valor numérico de cada dígito es alterado dependiendo de su posición en la cadena de dígitos, quedando multiplicado por una cierta potencia de la base del sistema, que en este caso es 16. Por ejemplo: 3E0A16 = 3×163 + E×162 + 0×161 + A×160 = 3×4096 + 14×256 + 0×16 + 10×1 = 15882.
El sistema hexadecimal actual fue introducido en el ámbito de la computación por primera vez por IBM en 1963. Una representación anterior, con 0–9 y u–z, fue usada en 1956 por la computadora Bendix G-15.
|
|
|
 Primer
Primer
 Anterior
2 a 15 de 105
Següent
Anterior
2 a 15 de 105
Següent Darrer
Darrer
|























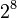 valores posibles, y esto puede representarse como
valores posibles, y esto puede representarse como 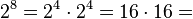
 , que equivale al número en base 16
, que equivale al número en base 16 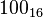 , dos dígitos hexadecimales corresponden exactamente a un byte.
, dos dígitos hexadecimales corresponden exactamente a un byte.