PYRAMIDE : Dimensions

Préambule

Personne n’a jamais retrouvé les plans de la grande pyramide, et le comble, c’est qu’ils sont nous nos yeux. Le plan avec les dimensions est inscrit dans la logique géométrique de la pyramide à base carrée. On retrouve aussi le plan dans la dimension de la chambre haute.

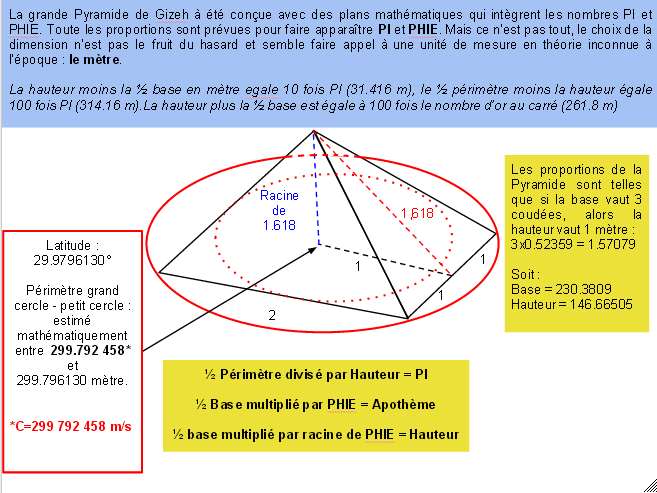
Il faut définir 2 dimensions au départ : largeur de la base carré et hauteur de la pyramide. Les dimensions de la pyramide peuvent être mesurées, mais la précision d’une construction n’est jamais parfaite, les outils de mesure non plus, et le temps à fait sont œuvre d’érosion, de tremblement de terre, de dilatation etc… Il est donc difficile de faire des mesures et d’affirmer : “la pyramide mesure 146,655 mètres”. En revanche, les btisseurs ont laissés des indices, car les mesures laissent apparaître des rapports et proportions qui nous indiquent le nombre Pi et le Nombre d’Or. Les mesures permettent de faire ressortir avec une approximation au centième, ou au millième de ces 2 constantes. Par exemple, les mesures physiques permettent de dire que le demi périmètre divisé par la hauteur est égale à (880 coudées / 280 coudées = 3.142857). Ce qui est très proche de PI (3.141592654…). Mais il faut maintenant raisonner en pensant comme des btisseurs, quelles dimensions veux t’ on donner à la pyramide. Les btisseurs ont voulut faire en sorte que les relations entre les dimensions permettent de faire ressortir exactement PI et exactement le PHIE du nombre d’Or avec la plus grande précision possible, même si ces nombres sont irrationnels, car ils ne s’arrête jamais.

Les plans de la Pyramide repose donc sur une logique mathématique faisant appel à 2 constantes de l’univers mathématique. Voici comment on peut retrouver ces 2 constantes.

• Le ½ périmètre de la pyramide au sol divisé par la hauteur au sol est égal à PI.

• La hauteur de la pyramide multiplié par la racine carré de PHIE est égale à l’apothème de la pyramide.
• La hauteur de la pyramide divisé par racine carré de PHIE égale la 1/2 base de la pyramide.

Avec ces informations que je schématise ci dessous les proportions de la grande pyramide.

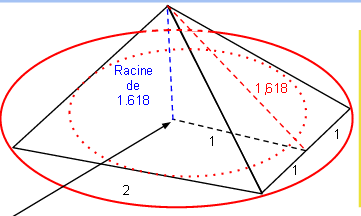
Problématique : La grande pyramide n’existe pas mathématiquement.

Si on prend des mesures, qu’on essaye d’être le plus précis possible on parvient à faire ressortie PIE et PHIE avec une précision intéressante. Par exemple, le 1/2 périmètre divisé par la hauteur nous donne 3,14, ce qui est proche de PIE. Mais si on essaye de raisonner en partant non plus des mesures de terrain, mais des constantes de l’univers que sont PI et PHIE en ajoutant par exemple 9 chiffres après la virgule, on s’aperçoit alors qu’il n’existe pas de Pyramide théorique capable de nous donner PIE et PHIE avec une précisions de 9 chiffres après la virgule.

En revanche, on peut essayer de voir quelles sont les dimensions théoriques qui nous donnent les valeurs les plus proches de PIE et PHIE.

La question est maintenant de trouver le meilleur compromis entre les dimensions de la pyramide pour obtenir une précision maximale des 2 constantes PI et PHIE.

Pyramide 1 : Si les dimensions nous donnent un nombre d’or parfait, alors PIE comporte une erreur importante, mais C, la vitesse de la lumière est d’une précision parfaite.

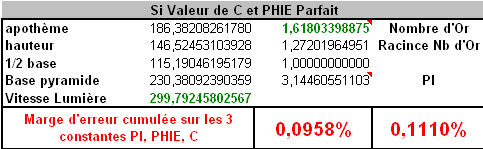
Pyramide 2 : Si les dimensions nous donnent un nombre PIE parfait, alors PHIE comporte une erreur moins importante que dans le cas précédent. La vitesse de la lumière, est là encore parfaite avec ce modèle.

Ce modèle est celui qui comporte le moins d’erreur mathématique. S’agit il du véritable plan voulu par les btisseurs de la Grande Pyramide ?

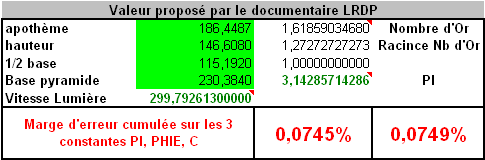
Pyramide 3, celle de Jacques Grimault : Celle ci est un compromis sur laquelle l’erreur théorique du modèle est répartie entre PIE, PHIE et C (vitesse de la lumière).

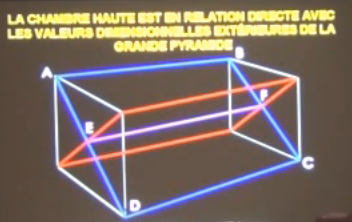
Pyramide 4 :

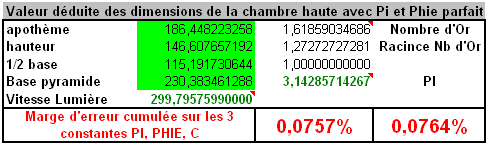
Pour celle ci, j’ai utilisé les dimensions de la chambre haute, qui je le rappel, sont en granite, un matériaux qui conserve ses dimensions dans le temps. Ainsi, la périmètre de la chambre haute fait référence à PIE : 31.416 m… et le périmètre moins un petit coté : PHIE carré : 26.180. En ayant compris que la chambre haute est aussi bti en faisant référence à PIE et PHIE on découvre que la hauteur et la largeur de la pyramide sont visible dans la chambre Haute. En effet, la hauteur de la pyramide est de 4 fois le périmètre du rectangle ABCD, soit 146.607657192 en utilisant PIE et PHIE avec 9 chiffres après la virgules. Quant à la base, elle est représenté par 4 fois le rectangle ouvert (3 cotés DABC), soit 115.191730643 m.

Bien, avec ces dimensions là, à quoi ressemble notre Pyramide ? Elle nous fournit une approximation intéressante de PIE, PHIE et C. Pour la vitesse de la lumière la marge d’erreur est de 0.00000516 %.

Pyramide de Georges Vermard et Mathieu Laveau :

Sur le très bon site internet horizon444, ces deux chercheurs libres ont développés une étude géométrique et mathématique très poussé du plateau de Gizeh. Ils retiennent des dimensions sensiblement différentes pour la base de la grande pyramide. Ainsi, au lieu de 230.384 m, il constate qu’elle mesure en théorie 230.291 m, soit un écart de 9.3 cm. Ce petit écart à l’air négligeable, mais il peut changer beaucoup de chose. Pour la hauteur ils proposent 146.608 tout comme Jacques Grimault, et d’autres auteurs officiel ou non.

Pour parvenir à ce résultat de 230,291, Georges Vermard et Mathieu Laveau, propose une équation différente. Pour eux, la 1/2 base de Khéops multiplié par 4/PIE est égale à la hauteur : (230,291 / 2) x (4 / PIE) = 146.608

Ils proposent dès lors un angle de 51°51’14 » contre un angle de 51°50’33.88″.

Voilà, mon petit exposé, repose sur des faits vérifiables, il suffit de se souvenir de vos cours de mathématiques et de géométrie. A la lumière de mes recherches, il me parait possible que la vitesse de la lumière ait volontairement été inscrite dans le monument.

Il me semble que la pyramide reposait sur des nombres entiers. Et 440 / 280 délivre à mon sens le véritable rapport de la grande pyramide de Khéops. La différence est faible entre les travaux de tout ces auteurs, mais il me semble plus probable que les dimensions de la Pyramide soient bien de 230.384 par 146.608 sans tenir compte du socle qui rajoute 1.10 m de large et une coudée de hauteur de 0.5236 m. Malgré cette petite différence, les calculs réalisés par les uns et les autres fonctionnent très bien si l’on accepte que la marge d’erreur se situe au delà de la virgule. La perfection n’existe vraiment pas, y compris dans la nature des choses.

http://messagedelanuitdestemps.org/index.php/pyramide-egypte/pyramides-dimensions/