|
|
KAVALA-GEMATRIA-NUMEROLOGIA BIBLICA-ETC: NUMERO 44=RESURRECCION DE LAZARO=44 HS VATICANO=HIPERCUBO=GESTACION BEBE
إختار ملف آخر للرسائل |
|
جواب |
رسائل 1 من 89 في الفقرة |
|
|
|
|
|
جواب |
رسائل 15 من 89 في الفقرة |
|
ISRAEL=ISIS-RA-ELOHIM / RA/ RELOJ/ RESURRECCION / LETRA R/ RAHABIT / RAQUEL (MADRE DE BENJAMIN (LOBO/ PERRO)
|
|
EL CONEJO ES SIMBOLO DE FERTILIDAD Y SE REPRODUCE CON EL NUMERO DE ORO
LA LEY DE LA RELATIVIDAD DE EINSTEIN TIENE QUE VER CON LA RELATIVIDAD DEL TIEMPO EN FUNCION A LA MASA Y LA VELOCIDAD DE LA LUZ
| Reply |
Message 52 of 52 on the subject |
|
|
|
|
|
MON-KEY/MON-DAY/MON-EY-E/LLAVE DEL MONO/MOON /LUNA/ RAQUEL (GENESIS 37)
|
|
|
|
جواب |
رسائل 16 من 89 في الفقرة |
|
|
|
|
جواب |
رسائل 17 من 89 في الفقرة |
|
|
|
|
جواب |
رسائل 18 من 89 في الفقرة |
|
|
|
|
جواب |
رسائل 19 من 89 في الفقرة |
|
|
|
|
جواب |
رسائل 20 من 89 في الفقرة |
|
LA TORRE DE BABEL, OSEA LA UNION ENTRE EL CIELO Y LA TIERRA, ES UN "AGUJERO DE GUSANO". EN ESTE MARCO ES EL GRIAL MISMO. SIMBOLIZA LA UNION ENTRE EL CIELO Y LA TIERRA, O LA CUADRATURA DEL CIRCULO (CIRCULO=CIELO; CUADRADO=TIERRA) O LA ESCUADRA Y EL COMPAS MASONICO. ES OBVIA LA CONNOTACION CON LA "ESCALERA DE JACOB". MAGDALENA TIENE CONNOTACION CON EL MISMO TERMINO TORRE EN HEBREO.
1. Josué 15:37 Zenán, HADASA, Migdal-gad,
2. Ester 2:7 Y había criado a HADASA, es decir, Ester, hija de su tío, porque era húerfana; y la joven era de hermosa figura y de buen parecer. Cuando su padre y su madre murieron, Mardoqueo la adoptó como hija suya.
ESTHER=ISHTAR=STAR GATE=PUERTA ESTELAR
BABEL=PUERTA DE DIOS

1 Pedro 5:13: La iglesia que está en Babilonia, elegida juntamente con vosotros, y Marcos mi HIJO, os saludan.
HECHOS 12:12 / 33 / JUAN MARCOS
ESTRELLA DE 6 PUNTAS = 33 = 2 TRIANGULOS CRUZADOS =ALQUIMIA
BABILONIA ESTABA EN EL PARALELO 33 Y ERA UNA CIUDAD DE 7 COLINAS.
BABEL/ BABY / BEBE /
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|
|
|
|
|
جواب |
رسائل 21 من 89 في الفقرة |
|
ABIMELEC (UN CASO BIBLICO DE TRASLACION EN EL TIEMPO)-JEREMIAS
CASO ABIMELEC (PARALIPOMENOS DE JEREMÍAS) -7-
 Habló entonces Jeremías: "Por favor, Señor, muéstrame qué puedo hacer por Abimelec el etíope, que practicó muchas obras buenas con tu siervo Jeremías; pues él me sacó de la cisterna de lodo y no deseo que vea la destrucción y desolación de esta ciudad, sino que tengas compasión de él y no se vea afligido". Y dijo el Señor a Jeremías: "Envíalo a la viña de Agripa, y a la sombra del monte yo le protegeré hasta que yo haga que el pueblo retorne a la ciudad."...
Llegado el amanecer, Jeremías envió a Abimelec diciendo: "Coge la cesta, parte hacia la finca de Agripa por el camino de la montaña, trae unos pocos higos y entrégalos a los enfermos del pueblo, pues el favor del Señor está sobre ti y su gloria sobre tu cabeza". Tras decir esto, Jeremías le despidió; y Abimelec marchó según le había dicho."...
Abimelec, por su parte, llevó los higos bajo un Sol ardiente, por lo que al encontrarse un árbol se sentó bajo su sombra para descansar un poco. Y al reclinar su cabeza sobre la cesta de los higos se durmió, quedando dormido durante sesenta y seis años sin despertarse de su sueño. Y después, al levantarse de su sueño, dijo: "He dormido a gusto un rato, pero mi cabeza está pesada porque no he quedado saciado con mi sueño". Entonces, al destapar la cesta de los higos, los encontró destilando leche. Y dijo: "Quería dormir todavía un poco, porque mi cabeza esta pesada; pero tengo miedo, no sea que me duerma, tarde en despertarme y mi padre Jeremías me menosprecie, pues si no tuviera prisa no me habría enviado hoy de madrugada. Así, pues, me pondré en pie y caminaré bajo el ardiente Sol, pues ¿no hay ardiente Sol, no hay fatiga todos los días?". Levantóse, por tanto, tomó la cesta de los higos, se la echó a los hombros y marchó a Jerusalén, pero no la reconoció ni su casa, ni su propio lugar , ni encontró a su propia familia ni a ninguno de sus conocidos. Y dijo: "¡Bendito sea el Señor, porque un gran éxtasis me ha sobrevenido hoy! Esta no es la ciudad de Jerusalén: he errado el camino porque fui por la senda del monte cuando me levanté de mi sueño; y como mi cabeza estaba pesada por no haber quedado saciado con mi sueño, he errado el camino. ¡Le parecerá sorprendente a Jeremías cuando le diga que he errado el camino!".
Entonces salió de la ciudad; y al fijarse bien vio los mojones de la ciudad y dijo: "Esta es ciertamente la ciudad; sin embargo, he errado el camino". Retornó de nuevo a la ciudad y se puso a buscar, pero no encontró a ninguno de los suyos. Dijo entonces: "Bendito sea e1 Señor, porque un gran éxtasis me ha sobrevenido.'". Salió nuevamente fuera de la ciudad y se quedó afligido, sin saber dónde ir. Y se quitó de encima la cesta, diciendo: "Voy a quedarme aquí sentado hasta que el Señor aparte de mi este éxtasis".
Mientras estaba él sentado, vio a cierto anciano que venia del campo; Abimelec le dice: "A ti te hablo, anciano, ¿qué ciudad es esta?". Le respondió: "Es Jerusalén". Abimelec le pregunta: "¿Dónde está Jeremías el sacerdote, Baruc el secretario y todo el pueblo de esta ciudad que no los he encontrado?". Repuso el anciano: "¿No eres de esta ciudad tú, que has recordado hoy a Jeremías, ya que preguntas por él tras tanto tiempo? Pues Jeremías está en Babilonia con el pueblo; fueron, en efecto, llevados cautivos por el rey Nabucodonosor, y con ellos está Jeremías para anunciarles buenas nuevas e instruirles en la palabra". Tan pronto como oyó esto Abimelec de aquel hombre anciano, dijo: "Si no fueras anciano, y como no le es lícito a un hombre encolerizarse con quien es mayor que él, me reiría de ti y te diría que estás loco, pues has dicho: "E1 pueblo ha sido llevado cautivo a Babilonia. ¡Aunque hubieran bajado sobre ellos los torrentes del cielo, no ha habido todavía tiempo suficiente para que hayan partido hacia Babilonia! Pues, ¿cuánto tiempo ha pasado desde que mi padre Jeremías me envió al campo de Agripa a traer unos pocos higos para que los diésemos a los enfermos del pueblo? Fui, los traje y al llegar hasta cierto árbol, bajo un Sol ardiente, me senté a descansar un poco, recliné mi cabeza sobre la cesta y me quedé dormido. A1 despertarme destapé la cesta de los higos, pensando que se me había hecho tarde, pero encontré los higos destilando leche, lo mismo que cuando los cogí. Tú, en cambio, dices que el pueblo ha sido llevado cautivo a Babilonia. Pero, para que te des cuenta, ¡toma, mira los higos!". Destapó la cesta de los higos al viejo y los vio destilando leche.
A1 verlos, el anciano dijo: "Hijo mío, hombre justo eres tú y no quiso Dios que vieras la desolación de la ciudad; por eso trajo este éxtasis sobre ti. Pues he aquí que hoy hace sesenta y seis años que fue llevado cautivo el pueblo de Babilonia. Y para que sepas, hijo, que es cierto cuanto te digo, alza los ojos hacia el campo y observa que no ha aparecido el crecimiento de las cosechas. Mira también los higos, que no es su tiempo, y date cuenta".

klockit.com
6" Star of David Theme Clock
750 × 735 - 65k - jpg |

amazon.com
STAR OF DAVID Wall Clock
355 × 355 - 34k - jpg |
185=37x5 (INDEPENDENCIA DE EEUU)
365=73X5 (DIAS EN EL GREGORIANO NO BISIESTO)
4/7 ES EL DIA NUMERO 185 DEL CALENDARIO GREGORIANO
1776=37X48
666=37X18
6. Apocalipsis 3:7: Escribe al ángel de la iglesia en Filadelfia: Esto dice el Santo, el Verdadero, el que tiene la LLAVE de David, el que abre y ninguno cierra, y cierra y ninguno abre:
1. Génesis 3:7 Entonces fueron abiertos los ojos de ambos, y conocieron que estaban desnudos; entonces cosieron hojas de HIGUERA, y se hicieron delantales.
31. Mateo 24:32 De la HIGUERA aprended la parábola: Cuando ya su rama está tierna, y brotan las hojas, sabéis que el verano está cerca.
|
|
|
|
جواب |
رسائل 22 من 89 في الفقرة |
|
|
|
|
جواب |
رسائل 23 من 89 في الفقرة |
|
The Great Pyramid and the Speed of Light
The Great Pyramid encodes enormous amount of numerical coincidences ( pi, Phi, dimensions and movement of our planet, axial tilt, precession, speed of light, and more…)
We can only wonder if the ancient architects were fully aware of these special numbers encoded in their design — or are these numbers simply the result of selecting 2 numbers (7 and 11) for proportions for the Great Pyramid???
|
|
The design of the Great Pyramid is based on the ratio 11:7. This ratio (equal 1.571) is perfect approximation of the “squaring the circle” principle.

For the Great Pyramid, Base to Height Ratio 440/280 is exactly 11/7
Most “pyramidologists” appear to be “chasing their tails” uncovering huge amount of “numerical coincidences” embedded in the Great Pyramid…
It is simply unbelievable, however ALL of these numerical coincidences are result of selecting just 4 numbers for the pyramid design: 7, 11 (height to base ratio), 40 (the scale factor), and the 4th key number is the value of the measuring unit: Royal Cubit = 20.62 ” = 0.524 m.
|
This single, fundamental design principle: 11 : 7 Base to Height Ratio generates ALL amazing mathematical properties of the Great Pyramid:
- the Golden Ratio Phi=1.618 (the Great Pyramid is a Golden Pyramid: length of the slope side (356) divided by half of the side (440/2 = 220) height is equal to 1.6181818… which is the Golden Ratio Phi
- squaring the circle ratio 1.571 (base/height = 44/28 = 1.571)
- pi=3.14159… (2 x base/height = 2 x 44/28 = 3.14286 which is very close approximation of “pi” = 3.14159…)
- Perimeter of the square base, 4×440=1760, is the same as circumference of the circle with radius = height: 2x ”pi” x height (2x 22/7 x 280=1760)
- The ratio of the perimeter to height of 1760/280 cubits equates to 2x pi
to an accuracy of better than 0.05%
- Side of the base (440) plus double height (2x 280=560) = 1,000
- Perimeter of the square base is equal 4×440=1760 RC = 0.5 nautical mile = 1/7,200th of the radius length of the earth
- the slop angle 51°.843
- The Pyramid exhibits in the design both pi and by Phi, given the similarity
of 2/ sqrt(phi) (2 divided by the square root of Phi) with pi/2 :
- 11/ 7 equal 1.5714
- 2/ sqrt(89/55) equal 1.5722
- 2/ sqrt(Phi) equal 1.5723
- pi/ 2 equal 1.5708
- Royal Cubit = 0.5236 m, pi – Phi2 = 0.5231
- and more…
Does Great Pyramid encode “fractal” value of the speed of light?
The speed of light in a vacuum is 299, 792, 458 meters per second or 983,571,056.43045 feet per second or 186,282.397 miles per second.
Base of the Great Pyramid is a square with side B = 44o Royal Egyptian Cubits. Let’s draw two circles: one inscribed and one superscribed on the square of the base of the Great Pyramid.

- Circumference of superscribed circle: 2x pi x R
- Circumference of the inscribed circle: 2x pi x r
The difference of the circumference of both circles (lets call it C) is:
C = 2 x pi x (R – r) = 2 x pi x [ B/sqrt(2) - B/2 ] =
2x pi x B x [ 1/sqrt(2) - 1/2 ] = 1.301290285 x B
The length of the Egyptian Royal Cubit
Based on “The Pyramids and Temples of Gizeh” by W.M. Flinders Petrie. 1883.
The unit of measuring length used by the ancient architects in the construction of the Great Pyramid was the Royal Cubit.
Petrie estimated the value of the Royal Cubit using some key dimensions of the Great Pyramid:
By the base length of the Pyramid, if 440 cubits (section ’43): 20.611 ± .002
By the base of King’s Chamber, corrected for opening of joints: 20.632 ± .004 inches
By the Queen’s Chamber, if dimensions squared are in square cubits: 20.61 ± .020
By the antechamber: 20.58 ± .020
By the ascending and Queen’s Chamber passage lengths (section 149): 20.622 ± .002
By the gallery width: 20.605 ± .032
The Average value of the RC (based on above numbers) is 20.61 inches.
It’s almost universally accepted that archaeologist Flinders Petrie’s determination of the royal cubit length at 20.632 inches, from his measurements of the King’s Chamber in the Great Pyramid of Giza, was the likely measure to survey the dimensions of that pyramid, 440 royal cubits per base side, but the experts stop there, not then letting you know that those 1,760 royal cubits which total the Great Pyramid’s base perimeter length, when multiplied by 20.632 inches, equals half a modern nautical mile, or 1/7,200th of the radius length of the earth, so there certainly is a connection.
EL EXAGONO Y LA RELACION CON EL PI=22/7-LAS MATEMATICAS CONFIRMAN LA RELACION EXAGONAL CON MARIA LA MAGDALENA EN EL MISMO DIA DE SU DIA EN LA IGLESIA CATOLICA, OSEA EL 22 DE JULIO (22/7)
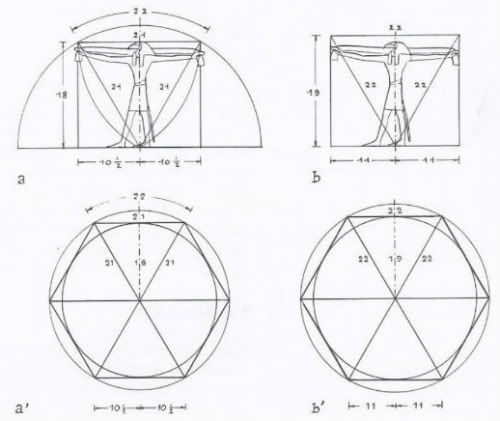 Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony West Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony West
Noten que tenemos el SECTOR CIRCULAR, en un contexto matematico exagonal, la relacion matematica 22/11. Sabemos que la longitud de la circunferencia es igual al numero PI=3.14=22/7 por el DIAMETRO=RADIO*2 del circulo. En un contexto a que tenemos segun la figura superior la LONGITUD DE ARCO (PI/3-RADIANES) que es igual a 22 si hacemos las matematicas:
LONG. CIRC.=3.14*DIAMETRO=3.14*2*RADIO=22/7*2*21=22/7*2*7*3=(22*2*7*3)/7=22*6
LONG. CIRC.=22*6=132=33*4 (IMPRESIONANTE RELACION DEL NUMERO 33)
Noten que estamos haciendo referencia al exagono y es obvia su interrelacion con el planeta Mercurio, que insisto, esta interrelacionada con la ESTRELLA DE DAVID, OSEA EL HIJO DEL MISMO DAVID, QUE FUE EL REY SOL-O-MON. El 33, insisto, es una referencia a los dos triangulos, de la estrella de 6 puntas. Ahora, si la longitud del arco es igual a PI/3 (RADIANES) tenemos la relacion:
22/21=22/(7*3)=(22/7)/3=PI/3
IMPRESIONANTE DE QUE BELLAS SON LAS MATEMATICAS.
LA MISMA PALABRA REVOLU-SION ES UNA REFERENCIA AL NUMERO PI (LONGITUD DE LA CIRCUNFERENCIA ES IGUAL A PI X DIAMETRO.)
|
| Reply |
Message 61 of 61 on the subject |
|
|
|
|
|
|
|
جواب |
رسائل 24 من 89 في الفقرة |
|
|
|
|
جواب |
رسائل 25 من 89 في الفقرة |
|
Teniendo en cuenta que el radio de la tierra promedio es de 7*12*12*12*12*12*12, la longitud de la circunferencia en este marco es de 44*12*12*12*12*12*12 tambien en pies ingleses. Osea que si cuadramos la LONGITUD DE LA CIRCUNFERENCIA DE LA TIERRA, TENEMOS UN CUADRADO CUYO LADO ES DE 11*12*12*12*12*12*12. VEMOS QUE AQUI TAMBIEN TENEMOS EL ORIGEN DE LA RELACION 11/7, CODIFICADA EN LA GRAN PIRAMIDE.
EL 12 ES UNA OBVIA REFERENCIA A LA SANTA CENA, EN EL MARCO AL LAVAMIENTO DE LOS PIES.
|
|
|
|
جواب |
رسائل 26 من 89 في الفقرة |
|
Washington DC: el Monumento a Washington = 8 y estrella octágono - la diosa sumeriana Inanna
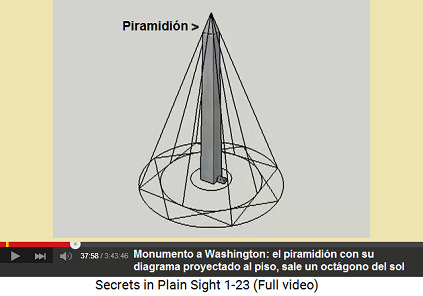 Monumento a Washington: el piramidión con su diagrama proyectado al piso, sale un octágono del sol
Bernard I. Pietsch detectó: las líneas alargadas de la pirámide de la punta (del piramidión pequeño) provocan un diagrama secreto en el piso con una estrella octagonal (38min.15seg.). Una estrella octagonal es el símbolo de la diosa sumeriana Inanna, la base de todas las leyendas de Isis (38min.29seg.). La civilización sumeriana fue solo detectada en 1890 (38min.42seg.). Así la ciencia esotérica ha ordenado todo a Isis lo que es en realidad conectado con Inanna (38min.48seg.).
Simbolismo de estrella de octagrama en todo el mundo
-- estrella de la diosa hindú Laksmí (39min.10seg.)
-- el grupo de 8 dioses de Egipto que forman la "ogdóada de Hermopolis" (Amun, Kauket, Amaunet, Hauhet, Naunet, Heh, Nun, Kuk, con el "huevo cósmico" en el centro con el dios solar Ra) (39min.19seg., 1h29min.36seg.).
-- calendario celta (39min.23seg.)
-- gnosticismo valentiano que convierta conceptos de Egipto en conceptos cristianos (39min.29seg.)
-- rueda budista de Dharma (39min.39seg.)
-- octagrama islámico: Rub el Hizb (39min.45seg.)
-- la iglesia ortodoxa también usa estrellas octagramas: Christ Pantocrater (39min.59seg.)
-- la piedra del calendario azteca en México (40min.7seg.)
-- el Vaticano [criminal satanista gay] usa el octágono en su patio y también usa un obelisco como pene en su centro [!] lo que trabaja como reloj solar (40min.23seg.).
En total la estrella de octagrama es un símbolo solar (40min.35seg.).
Monumento de Washington: mediciones de los órganos sexuales femeninos - y la Gran Pirámide de Guiza
La energía femenina del Monumento a Washington es representada con las líneas de un pez "vesica piscis" (40min.46seg.) que representan las piernas de una mujer con su vulva (41min.5seg.). Cuando los círculos de un pez de círculos (vesica piscis) son agrandados hasta al diámetro de la altura del obelisco (sale un diámetro de 555' (pies)) así la Gran Pirámide de Guiza sale exactamente en esa "vulva" (41min.6seg.) con una altura de 481 y 1/11 pies (481'+1/11') (41min.13seg.). Qué coincidencia. El arquitecto del Monumento a Washington debe haber tenido conexiones con los pirámides de Egipto (41min.16seg.).
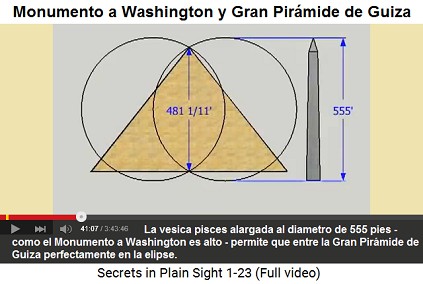 La elipse de pez agrandada del Monumento a Washington a un diámetro de 555' (pies) permite que la Gran Pirámide de Guiza entre perfectamente en esa elipse.
Las proporciones de la Gran Pirámide de Egipto y del obelisco del Monumento a Washington tienen una conexión directa:
-- altura del obelisco del Monumento a Washington (555') = largo inclinado de la Gran Pirámide (555') (41min.20seg.)
-- radio del piramidión proyectado al piso = medio radio de la Gran Pirámide (41min.20seg.)
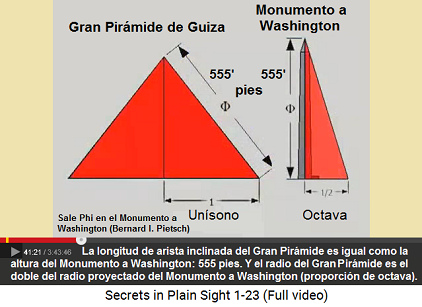 Esquema: el largo inclinado de la Gran Pirámide de Guiza es la altura del Monumento a Washington (555 pies), y el radio de la Gran Pirámide es el doble del radio proyectado del piramidión del Monumento a Washington
Washington DC: el patio trasero de la Casa Blanca es como Stonehenge
El patio trasero de la Casa Blanca tiene la misma forma de "U" como la estructura interior de Stonehenge (41min.43seg.).
 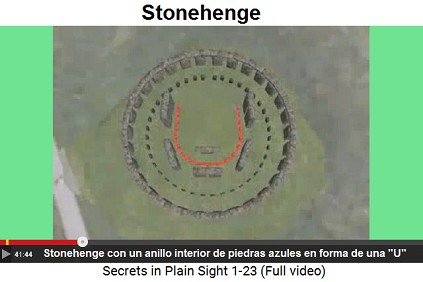 El patio trasero de la Casa Blanca está en forma de una "U" como Stonehenge tiene - Stonehenge con un anillo interior de piedras azules en forma de una "U"
Y los dos triángulos alrededor de la Casa Blanca forman un rectángulo de 5:12 (41min.50seg.). Esas proporciones son las mismas como el rectángulo de piedras de estaciones (41min.53seg.).
  La Casa Blanca con una "U" y triángulos con proporciones 5:12 - Stonehenge con una "U" y con el triángulo de estaciones 5:12 [Conclusión: La Casa Blanca es otro Stonehenge y extraterrestres de Stonehenge están gobernando la Casa Blanca].
Una línea directa de la punta del "Triángulo Federal" de Washington DC al centro de Stonehenge en Inglaterra nos muestra que la línea cruce el Parque Central de Nueva York (42min.9seg.) precisamente en otro ángulo con la proporción de 5:12 (42min.27seg.).
 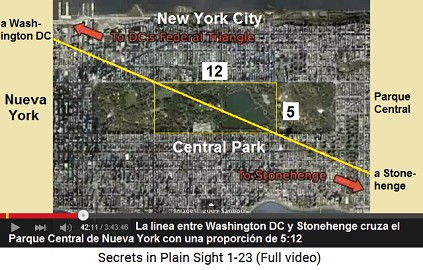 Línea directa de Washington a Stonehenge - La línea entre Washington DC y Stonehenge cruza el Parque Central de Nueva York con una proporción de 5:12 |
|
|
|
جواب |
رسائل 27 من 89 في الفقرة |
|
Sólido de Kepler-Poinsot
Los sólidos de Kepler-Poinsot con sus símbolos de Schläfli.
Un sólido de Kepler (también llamado sólido de Kepler-Poinsot) es un poliedro regular no convexo, cuyas caras son todas polígonos regulares y que tiene en todos sus vértices el mismo número de caras concurrentes (compárese con los sólidos platónicos).
Existen sólo cuatro tipos, con las denominaciones siguientes:
Las caras están solo parcialmente en la superficie del sólido, y las partes expuestas están sólo conectadas en puntos (si están conectadas de algún modo). Si las partes se cuentan como caras separadas, el sólido deja de ser regular.
Características
Un sólido de Kepler cubre su esfera circunscrita más de una vez (con una esfera interior y otra exterior), con los centros de las caras como puntos direccionales en los sólidos que tienen caras en forma de pentagrama, mientras que en los otros son los vértices los que cumplen esa función. Por esta razón, no son necesariamente equivalentes topológicos de la esfera como lo son los sólidos platónicos, y en particular la característica de Euler V − E + F = 2 se verifica solamente para el Gran dodecaedro estrellado y para el Gran icosaedro.
Esto dependerá de cómo se observe el poliedro. Considérese, por ejemplo, el pequeño dodecaedro estrellado.1 Consiste en un dodecaedro con una pirámide pentagonal en cada una de sus 12 caras. En consecuencia, las 12 caras se extienden a pentagramas con el pentágono central dentro del sólido. La parte externa de cada cara consiste en cinco triángulos conectados por sólo cinco puntos. Si se cuentan separadamente, hay 60 caras (pero estas son triángulos isósceles que no son polígonos regulares, en cuyo caso seria un pentaquisdodecaedro). De modo similar, cada lado puede ser contado como tres, pero entonces los habrá de dos tipos. Igualmente, con los "cinco puntos" antes mencionados: en total habrá 20 puntos que pueden contarse como vértices, por lo que habrá un total de 32 vértices (otra vez, de dos tipos). Ahora la ecuación de Euler se verifica: 60 - 90 + 32 = 2.
Tipos
Hay cuatro sólidos de Kepler distintos:
Los dos primeros son estrellamientos, es decir, sus caras son convexas. Los otros dos tienen caras cóncavas, pero cada par de caras que se encuentra en un vértice de hecho lo hace en dos.
Historia
Mosaico del suelo en la basílica de San Marcos, a veces atribuido a Paolo Uccello.
La mayoría de los poliedros de Kepler-Poinsot, si no todos, eran ya conocidos de una forma u otra antes de Kepler. Un pequeño dodecaedro estrellado aparece en una tarsia de mármol (panel de incrustaciones) en el suelo de la basílica de San Marcos de Venecia, Italia. Data del siglo XV y, a veces se atribuye a Paolo Uccello. Wenzel Jamnitzer, en su obra Perspectiva corporum regularium (Perspectivas de los sólidos regulares), un libro de grabados en madera publicado en el siglo XVI, representa el gran dodecaedro y el gran dodecaedro estrellado.2 Se desprende de la disposición general del libro que consideraba solamente los cinco sólidos platónicos como regulares, y no comprendía la naturaleza periódica de sus grandes dodecaedros.
El pequeño y gran dodecaedro estrellado, a veces llamados poliedros de Kepler, fueron reconocidos por primera vez como regulares por Johannes Kepler en 1619, cuando notó que los dodecaedros estrellados (tanto el grande como el pequeño) se componían de dodecaedros "ocultos" (con caras pentagonales) que tienen caras compuestas de triángulos, tomando la apariencia de estrellas estilizadas. Los obtuvo por estelación del dodecaedro regular convexo, por primera vez, tratándolo como una superficie en lugar de un sólido. Se dio cuenta de que extendiendo los bordes o caras del dodecaedro convexo hasta que se encontrasen de nuevo, se podían obtener pentágonos estrellados. De esta manera construyó los dos dodecaedros estrellados, cada uno con la región convexa central de cada cara "oculta" en el interior, sólo con los brazos triangulares visibles. El paso final de Kepler fue reconocer que estos poliedros se ajustaban a la definición de regularidad, aunque fueran cóncavos en lugar de convexos, como sí lo eran los tradicionales sólidos platónicos.
En 1809, Louis Poinsot redescubrió las figuras de Kepler, mediante el ensamblaje de pentágonos estrellados alrededor de cada vértice. También montó polígonos convexos alrededor de los vértices de las estrellas para descubrir dos estrellas más regulares, el gran icosaedro y el gran dodecaedro. Por ello, algunos llaman a estos dos los poliedros de Poinsot. Poinsot no sabía si había descubierto todos los poliedros regulares estrellados.
Tres años más tarde, Augustin Cauchy demostró que la lista por estelación de los sólidos platónicos estaba completa, y casi medio siglo después, en 1858, Joseph Louis François Bertrandproporcionó una prueba más elegante por facetado de ellas.
Al año siguiente, Arthur Cayley dio a los poliedros de Kepler–Poinsot los nombres por los que generalmente conocidos hoy.
Unos cien años más tarde, John Conway desarrolló una terminología sistemática para las estelaciones hasta un máximo de cuatro dimensiones. Dentro de este esquema, sugirió nombres ligeramente modificados para dos de los poliedros regulares estrellados. Los nombres de Conway han sido considerados de utilidad, pero no han sido ampliamente adoptados.
| Nombre de Cayley |
pequeño dodecaedro estrellado |
gran dodecaedro |
gran dodecaedro estrellado |
gran icosaedro |
| Nombre de Conway |
dodecaedro estrellado |
gran dodecaedro (sin cambio) |
dodecaedro grande estrellado |
gran icosaedro (sin cambio) |
https://es.wikipedia.org/wiki/S%C3%B3lido_de_Kepler-Poinsot |
|
|
 First First  Previous 2 to 5 of 5 Next Previous 2 to 5 of 5 Next  Last Last  |
|
|
Posted in Azulejos-Mosaicos, Italia, Templo with tags Poliedros on 7 junio 2012 by angelrequena

Hace tiempo hablamos del conocido pequeño dodecaedro estrellado del pavimento de la puerta de salida derecha del duomo de San Marcos. No es el único de la catedral veneciana: apenas visible para la visita ordinaria hay otro más pequeño, justo debajo del iconostasio en su centro, en lugar preferente y en línea con el altar.
Si se entra hacia la Pala de Oro puede verse una mancha central en la lejanía pero casi sin distinguirse. En mi última visita tuve la gran suerte de encontrar un ordenanza amable que encendía las luces a un grupo concertado que me permitió verlo y fotografiarlo. No desmerece de su hermano mayor, si cabe revela mayor virtuosismo y ostentación del dominio de la perspectiva matemática.
Hay cuatro sólidos regulares cóncavos, los dos de Poinsot y los dos de Kepler. Venecia nos ofrece los dos de Kepler en San Pantaleone y uno en San Marcos pero en dos lugares, uno alejado para despedirse del templo y otro en el lugar más destacado: la entrada central al recinto más sagrado.
El dodecaedro estrellado de la puerta (abajo) solo tiene una corona de taracea marmórea complementaria mientras que el del iconostasio (arriba) tiene tres.

3 Comments »
https://mateturismo.wordpress.com/tag/poliedros/page/7/
|
|
|
|
|
|
|
جواب |
رسائل 28 من 89 في الفقرة |
|
|
|
|
جواب |
رسائل 29 من 89 في الفقرة |
|
. Juan 16:21 La mujer cuando da a luz, tiene dolor, porque ha llegado su HORA; pero después que ha dado a luz un niño, ya no se acuerda de la angustia, por el gozo de que haya nacido un hombre en el mundo.
|
|
|
 أول أول
 سابق
15 a 29 de 89
لاحق سابق
15 a 29 de 89
لاحق آخر
آخر
|
|
| |
|
|
©2026 - Gabitos - كل الحقوق محفوظة | |
|
|

