|
Rispondi |
Messaggio 1 di 1558 di questo argomento |
|
TABERNACULO =TEMPLO DE SALOMON = KAABA = GIZE= VATICANO= WASHINGTON D.C = NUEVA JERUSALEN = JUAN MARCOS
CENACULO DE JERUSALEN=SAN MARCOS
"AGUJERO DE GUSANO MUNDIAL" ES VESICA PISCIS. NEXO CON EL CUBO
En diversos periodos de la historia ha sido tema de especulaciones místicas; probablemente los primeros fueron los Pitagóricos, que la consideraban una figura sagrada. La razón matemática de su anchura (medida por los puntos extremos del "cuerpo", sin incluir la "cola") por su altura fue aproximada por el cociente 265:153. Esta razón, que da 1,73203, se consideró un número sagrado llamado la medida del pez. Exactamente, la razón geométrica de estas dimensiones es la raíz cuadrada de 3, o 1,73205... (ya que si se traza la línea recta que une los centros de ambos círculos, junto con los dos puntos donde los círculos se intersecan, se obtienen dos triángulos equiláteros unidos por un lado). El cociente 265:153 es una aproximación a la raíz cuadrada de 3, y tiene la propiedad de que no se puede obtener ninguna aproximación mejor con números más pequeños. El número 153 aparece en el Evangelio de Juan (21:11) como el número de peces que Jesús hizo que se capturaran en la milagrosa captura de los peces, lo que algunos consideran como una referencia cifrada de las creencias pitagóricas.

APOCALIPSIS 21
NU-EVA J-ER-U-S-A-LE-N /JUAN
EVA (NUMERO NU-EVE)=MARIA MAGDALENA O MARIA LA GRANDE
JUAN MARCOS=SANTO GRIAL
9. Vino entonces a mí uno de los siete ángeles que tenían las siete copas llenas de las siete plagas postreras, y habló conmigo, diciendo: Ven acá, yo te mostraré la desposada, la esposa del Cordero. (Noten la relacion de la COPA CON LA ESPOSA DEL CORDERO)
10. Y me llevó en el Espíritu a un monte grande y alto, y me mostró la gran ciudad santa de Jerusalén, que descendía del cielo, de Dios,
11. teniendo la gloria de Dios. Y su fulgor era semejante al de una piedra preciosísima, como piedra de jaspe, diáfana como el cristal. (LA "GLORIA DE DIOS" es una clave sabatica en contexto a EXODO 24 Y 25. Se vuelve a repetir el patron del libro de EFESO EN SU CAPITULO 5.)
12. Tenía un muro grande y alto con doce puertas; y en las puertas, doce ángeles, y nombres inscritos, que son los de las doce tribus de los hijos de Israel;
13. al oriente tres puertas; al norte tres puertas; al sur tres puertas; al occidente tres puertas.
14. Y el muro de la ciudad tenía doce cimientos, y sobre ellos los doce nombres de los doce apóstoles del Cordero.
ESTRELLA DE DAVID ES LA ALQUIMIA, OSEA LA UNION ENTRE EL HOMBRE Y LA MUJER
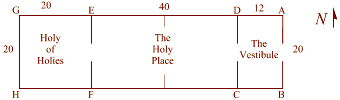
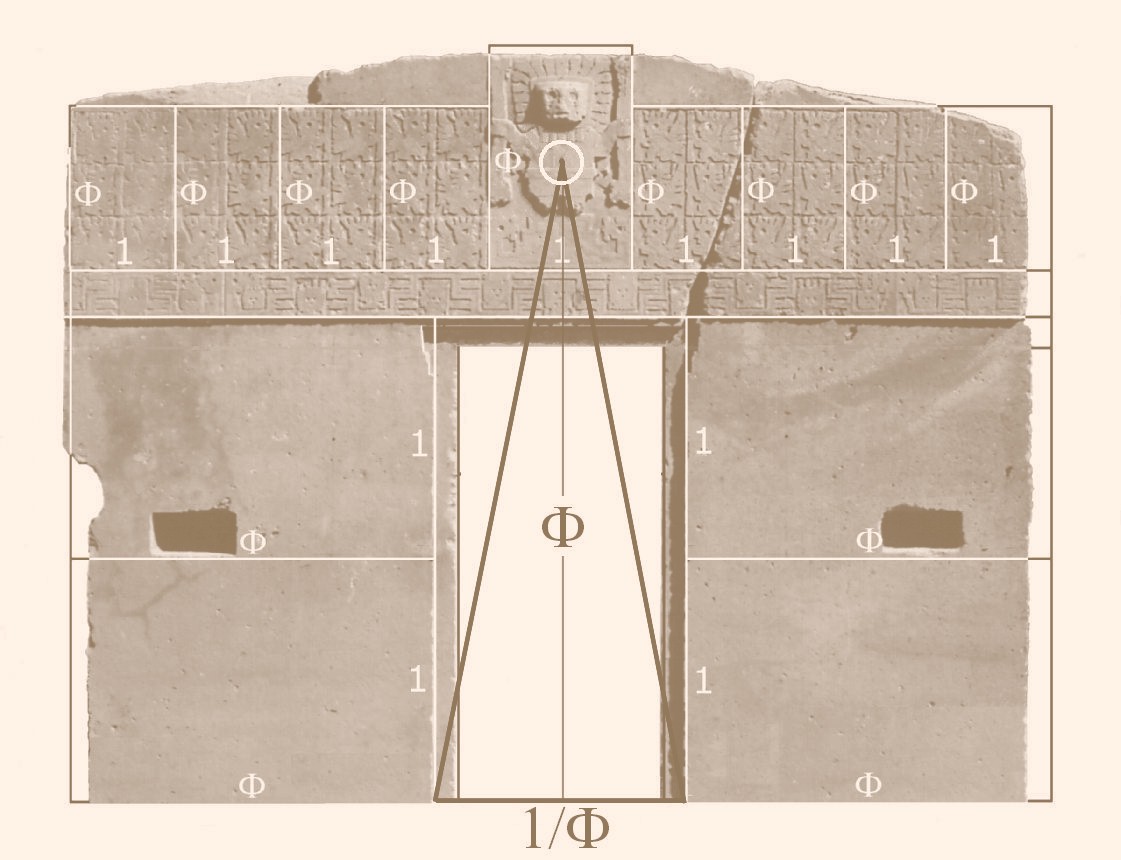
(ABCD) Double Square in Solomons Temple
EL LUGAR SANTISIMO DEL TABERNACULO Y DEL TEMPLO DE SALOMON TENIA FORMA DE CUBO
NOTEN LA ESTRELLA DE 5 PUNTAS EN EL CENTRO DEL EXAGONO CENTRO DE LA ESTRELLA DE 6 PUNTAS
EL EXAGONO TAMBIEN ES UNA REFERENCIA AL CUBO.
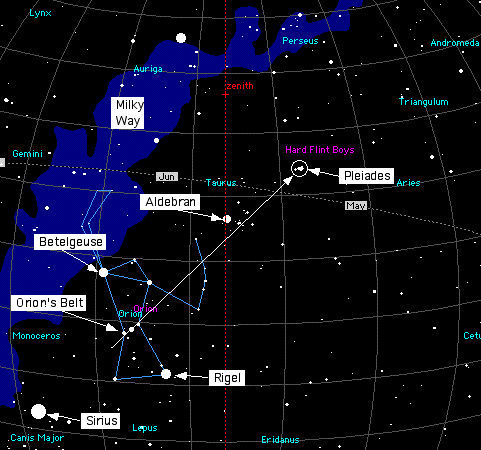
NOTEN QUE EN ESTA ESTRELLA DE 6 PUNTAS HAY 13 TRIANGULOS DE 5 PUNTAS, OSEA QUE NOS DA UN NEXO CON LAS 12 CONSTELACIONES DEL ZODIACO, CON LAS 12 HORAS DEL DIA, CON LAS 12 LUNAS QUE HAY EN EL CALENDARIO, CON LA SANTA CENA EN EL CONTEXTO A LOS 12 APOSTOLES, CON LAS 12 TRIBUS DE ISRAEL, CON EL MERIDIANO DE GREENWICH E INCLUSO CON ROSE LINE, ETC,ETC. TODO TIENE COMO PATRON LA ESTRELLA DE 6 PUNTAS, OSEA LA UNION ENTRE EL HOMBRE Y LA MUJER QUE LA TRADICION RELIGIOSA "OLVIDO". ESTE ES EL PATRON ESOTERICO DETRAS DE APOCALIPSIS 22 EN SU RELACION CON VENUS.

Noten el MONSTRUOSO NUMERO 36, incluso con la FORMA DE ORION, en una estrella de 6 puntas. Son siete pelotitas, con 6 perimetrales. 6x6=36
AQUI ESTA EL ULTRA SECRETO DEL NEXO 666 CON LA PIRAMIDE DE LOUVRE, EN EL CODIGO DA VINCI. 1+2+3+ 4+5+6+7+8+9 +20+11+12+13 +14+15+16+17+18 +19+20+21+22+23 +24+25+ 26+27+28+29 +30+31 +32+33+ 34+35 +36=666

15. El que hablaba conmigo tenía una caña de medir, de oro, para medir la ciudad, sus puertas y su muro.
16. La ciudad se halla establecida en cuadro, y su longitud es igual a su anchura; y él midió la ciudad con la caña, doce mil estadios; la longitud, la altura y la anchura de ella son iguales. (LA CUBICACION DE UNA ESFERA. HAY UN OBVIO NEXO ALQUIMICO. LA GRAN CIUDAD ESTA DISEÑADA CON EL MISMO PATRON DE LA GRAN PIRAMIDE DE GIZE)

Figura 16. La relación geométrica entre el codo real y el metro.
LA CLAVE MATEMATICA ESTA EN LA ECUACION:
PI-(PHI ELEVADO AL CUADRADO)=CODO REAL
 |
|
3.1416 - 2.61800 = 0.5236
|
3.1416-2.618=0.5236
CODO REAL=.5236
ESTE ES EL SECRETO DEL NEXO "ROSE LINE", EN EL CONTEXTO AL METRO Y EN EL CONTEXTO A LA PIRAMIDE DE LOUVRE.
17. Y midió su muro, ciento cuarenta y cuatro codos, de medida de hombre, la cual es de ángel.
21. Las doce puertas eran doce perlas; cada una de las puertas era una perla. Y la calle de la ciudad era de oro puro, transparente como vidrio.
22. Y no vi en ella templo; porque el Señor Dios Todopoderoso es el templo de ella, y el Cordero.
23. La ciudad no tiene necesidad de sol ni de luna que brillen en ella; porque la gloria de Dios la ilumina, y el Cordero es su lumbrera.


Haz clic en la imagen para volver
INICIACIÓN A LOS NÚMEROS DE LA ARQUITECTURA O DE COMO DARLE FORMA A UN EDIFICIO
Los números pueden estar explicados matemáticamente en la “red” pero el problema que plantea el conocimiento de la arquitectura es: ¿cómo se le da forma con esos números a un edificio?. En arquitectura los números operan a partir de los polígonos estrellados formando concatenaciones, tal y como a continuación vamos a describir.

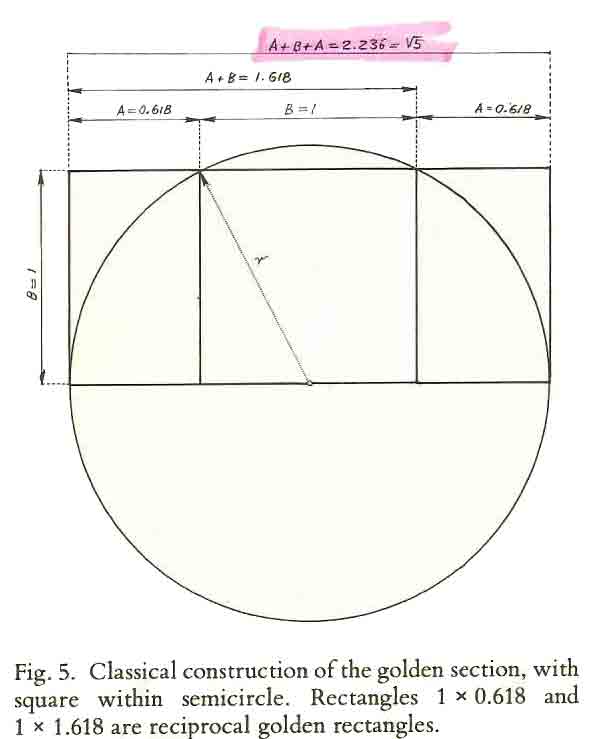
NÚMERO DE ORO - PENTÁGONO
El número de oro viene dado por la solución a la ecuación de segundo grado
x + x² = 1 x = 1+√5 /2 = 1,618033989
Propiedades 1/ 1,618 = 0,618 1,618... x 1,618... = 2,618...
Dado una circunferencia de radio 1 el lado del decágono inscrito en él es 0,618...
Dado un pentágono de lado 1, las diagonales de ese pentágono = 1,618...
La técnica con la que opera la arquitectura es la de las concatenaciones.
Una de ellas, la más usual, es la que presentamos en el dibujo. Si la circunferencia en color azul tiene R=1 el radio de la roja es R= 2,618, correspondiente a la que presentamos en “El vitruvio” de Leonardo da Vinci en la portada de este trabajo.
Se aplicará en la restitución de una tabla de F. Brunelleschi Nº 6.
 
NÚMERO DE PLATA - EL OCTÓGONO
Así como el número de oro está asociado a la √5 el número de plata está asociado a √2 y presenta una serie de propiedades similares a las del número de oro.
√2 = 1,414213562 tg. 22,5º = 0,414213562
tg.67,5º = 2,414213562
1/2,4142... = 0,4142... 2,4142... x 1,4142... = 3,4142...
Observa nuevamente la concatenación, esta vez con el octógono, de la circunferencia en color azul sobre la de color rojo.
Si el radio de la circunferencia azul es 1 la de color rojo es 2,4142....
Si el radio de la circunferencia azul es 0,4142... la de rojo es 1.
Aquí tenéis un ejemplo.
Se aplicará en la Rix House de J. Soane Nº 3.
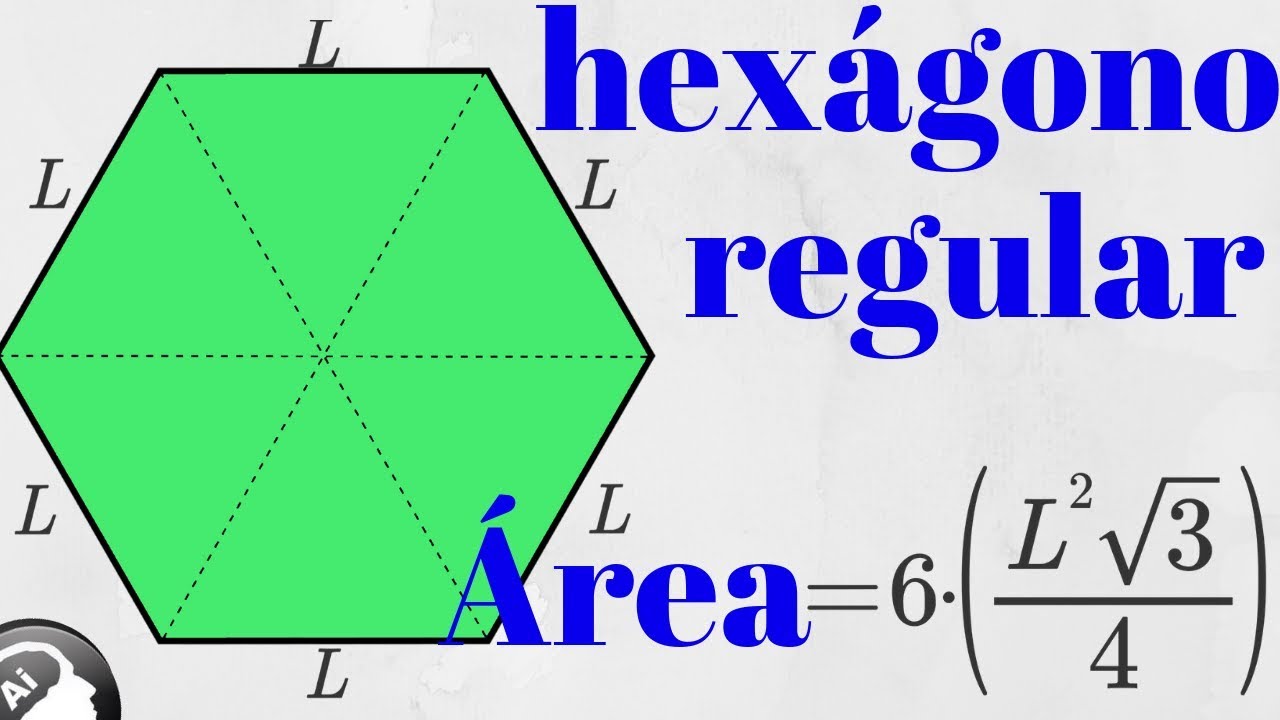
NÚMERO DE PLATINO - EL HEXÁGONO
De igual forma que el número de oro está relacionado con la √5 y el de plata con la √2, el de platino lo va a estar con la √3
√3 = tg.60º = 1,732050808
1,732... x 2,732... = 4,732...
Combinación, esta, muy utilizada por Andrea Palladio.
Observa la concatenación de la circunferencia azul sobre la de rojo, a través del hexágono, directamente a la circunferencia azul. Si el radio de la circunferencia color azul es 1 el de la circunferencia en color rojo es 2 y el lado del triángulo inscrito es 2 x 1,732...
Este polígono es el más prolífico en la historia de arquitectura como vamos a verlo en los ejercicios.
Aquí tenéis un ejemplo.
Se aplicará al resto de los trabajos Nº 1 - 2 - 4 y 5.
Todos los derechos reservados. Depósito Legal ZA - Nº 69 - 1998
Página web optimizada para ver en resolución de 1024 x 768
2006 - 2007
|
|
|
|
Rispondi |
Messaggio 1454 di 1558 di questo argomento |
|

Contribution (in agreement) by Liddz:
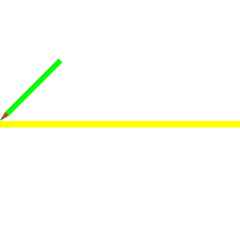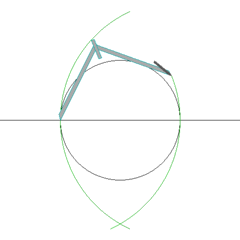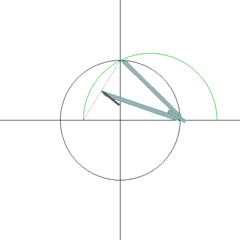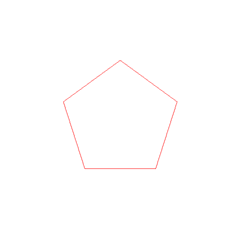
To get the correct measure for a circle’s diameter and to prove that Golden Pi = 4/√φ = 3.144605511029693144 is the true value of Pi by
applying the Pythagorean theorem to all the edges of a Kepler right triangle when using the second longest edge length of a Kepler right triangle as the diameter of a circle then the shortest edge length of a Kepler right triangle is equal in measure to 1 quarter of a circle’s
circumference. Also if the radius of a circle is used as the second longest edge length of a Kepler right triangle then the shortest edge length of a Kepler right triangle is equal to one 8th of a circle’s circumference:
Example 1:
The circumference of the circle is 12 but the measure for the diameter of the circle is not yet known. To discover the measure for the diameter of the circle apply the Pythagorean theorem to both 1 quarter
of the circle’s circumference and also the result of multiplying 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. Divide the diameter of the
circle by the square root of the Golden ratio = 1.272019649514069 to confirm that the edge of the square that has a perimeter that is equal to the numerical value for the circumference of the circle is equal to 1 quarter of the circle’s circumference.
Multiply the edge of the square by 4 to also confirm that the perimeter of the square has the same numerical value as the circumference of the circle.
Divide the measure for the circumference of the circle by the measure for the diameter of the circle to discover the true value of Pi. Multiply Pi by the diameter of the circle to also confirm that the circumference of the circle has the same numerical value as the perimeter of the square.
The second longest edge length of a Kepler right triangle is used as the diameter of a circle in this example. 12 divided by 4 is 3 so the shortest edge length of the Kepler right triangle is 3. The hypotenuse
of a Kepler right triangle divided by the shortest edge length of a Kepler right triangle produces the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.
According to the Pythagorean theorem the hypotenuse of any right triangle contains the sum of both the squares on the 2 other edges of the right triangle.
The shortest edge length of the Kepler right triangle is 3 and since the ratio gained from dividing the hypotenuse of a Kepler right triangle by the measure for the shortest edge of the Kepler right triangle is the Golden ratio of Cosine (36) multiplied by 2 =
1.61803398874989 then the measure for the hypotenuse of a Kepler right triangle that has its shortest edge length as 3 is 4.854101966249685.
4.854101966249685 divided by 3 is the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.
The square root of the Golden ratio = 1.272019649514069
4.854101966249685 squared is 23.562305898749058.
3 squared is 9.
23.562305898749058 subtract 9 = 14.562305898749058
The square root of 14.562305898749058 is 3.816058948542208.
Remember that the second longest edge length of the Kepler right triangle is used as the diameter of a circle. The measure for both the second longest edge length of this Kepler right triangle and the diameter of the circle is 3.816058948542208.
Remember that the shortest edge length of this Kepler right triangle is 3 and is equal to 1 quarter of a circle’s circumference that has a measure of 12 equal units.
Circumference of circle is 12
Diameter of circle is 3.816058948542208.
Diameter of circle is 3.816058948542208 divided by the square root of the Golden ratio = 1.272019649514069 = 3 the edge of the square.
3 multiplied by 4 = 12.
The perimeter of the square = 12.
12 divided by 3.816058948542208 = Golden Pi = 3.144605511029693144.
4/√φ = Pi = 3.144605511029693144 multiplied by the diameter of the circle = 3.816058948542208 = 12.
The circumference of the circle is the same measure as the perimeter of the square.
4/√φ = 3.144605511029693144 is the true value of Pi.
PYTHAGOREAN THEOREM: https://en.wikipedia.org/wiki/Pythagorean_theorem
Ver menos
|
|
|
|
Rispondi |
Messaggio 1455 di 1558 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 1456 di 1558 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 1457 di 1558 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 1458 di 1558 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 1459 di 1558 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 1460 di 1558 di questo argomento |
|


Eye within an interlocking circle and triangle
The 18th century church of Santa Maria della Maddalena (1763-90), better known simply as La Maddalena, was designed by the Venetian architect Tommaso Temanza (1705-89).
The entrance to the church is surmounted by the inscription SAPIENTIA AEDIFICAVIT SIBI DOMUM (Wisdom has built herself a home) and a curious image of an eye surrounded by an interlocking circle and triangle.
The all-seeing eye is one of the symbols of freemasonry and both the architect and the patron (a member of the Baffo family) of the church were freemasons.
Temanza's ashes are interred in La Maddalena.

La Maddalena

La Maddalena

Tomb of Tommaso Temanza https://www.picturesfromitaly.com/venice/freemasonry-and-the-church-of-santa-maria-della-maddalena-venice
 the Apple
|
|
|
|
Rispondi |
Messaggio 1461 di 1558 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 1462 di 1558 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 1463 di 1558 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 1464 di 1558 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 1465 di 1558 di questo argomento |
|
|
|
|
Rispondi |
Messaggio 1466 di 1558 di questo argomento |
|
 
Estimado lector que rozas una vez más la suave y policromada pluma del Tocororo:
Albert Einstein, Premio Nobel de Física, el científico más importante del siglo XX y posiblemente el segundo de toda la humanidad (el primero es Isaac Newton sin duda alguna) , visitó La Habana el 21 y 22 de diciembre de 1930. Su estancia en la capital se debió a que el Belgenland, barco en que viajaba desde la ciudad holandesa de Amberes, hizo escala en el puerto de La Habana antes de cruzar por el canal de Panamá con destino a la ciudad de San Diego, en la costa norteamericana del Pacífico. En este último lugar lo recibiría Edwin Hubble.
Hubble fue uno de los más importantes astrónomos estadounidenses del siglo XX, famoso principalmente porque en 1929 había demostrado la expansión del universo midiendo el corrimiento hacia el rojo de las galaxias distantes. Hubble es considerado el padre de la cosmología observacional aunque su influencia en astronomía y astrofísica tocó muchos otros campos.
Un poquito de Física: Cuando un tren se acerca a nosotros a gran velocidad haciendo sonar su silbato, notamos una subida en el tono de su sonido (la frecuencia aumenta) pero cuando el tren se aleja de nosotros apreciamos una bajada de ese tono (la frecuencia disminuye). Este fenómeno se conoce como Efecto Doppler y también se produce en el caso de la luz de forma que si miramos hacia una estrella que se acerca a gran velocidad percibimos su luz con un tono azulado pero si se aleja, ese tono sería rojizo. A esto se le llama corrimiento hacia el rojo.
El efecto Doppler puede usarse para medir la velocidad de los coches en la carretera utilizando ondas de radio de onda muy corta. (RADAR).
El propio Einstein, quien creía en un principio en un universo estático, introdujo de forma artificial un término extra a sus ecuaciones, denominado constante cosmológica, para evitar el fenómeno de la expansión. Tras los resultados publicados por Hubble, Einstein se retractó y retiró este término, al que llamó “el mayor error de mi carrera“. Einstein hizo entonces un famoso viaje a Monte Wilson en 1931 para agradecer a Hubble que hubiera sentado las bases de la cosmología moderna.
La alegría de los científicos cubanos de conocer y dialogar con el más notable de los físicos de todo el mundo era tan grande como la preocupación que tenían por la tensa situación social y política que vivía Cuba. Eran tiempos en que el General Gerardo Machado, apoyado por las fuerzas represivas y el apadrinamiento del gobierno yanqui, había prorrogado su mandato presidencial convirtiéndolo en una cruel dictadura. El descontento popular crecía y los estudiantes y revolucionarios se organizaban para enfrentar valientemente a aquel odioso y sangriento régimen. Hacía pocas semanas que en una protesta popular contra el gobierno las balas de la policía habían asesinado a Rafael Trejo, uno de los líderes universitarios más queridos y para colmo, la Universidad acababa de ser clausurada por decreto presidencial.
Los dirigentes de la Academia de Ciencias Médicas, Físicas y Naturales de La Habana y de la Sociedad Geográfica de Cuba trataron de hacer todo lo posible para disimular aquella realidad y darle el tratamiento que correspondía a tan distinguida y singular personalidad. A las ocho de la mañana del día 21 abordaron el barco para darle la bienvenida. También había decenas de periodistas.
Einstein agradeció el saludo de los académicos, dijo algunas palabras a los reporteros y posó para los fotógrafos y camarógrafos cubanos y extranjeros.
Aunque era el mes de diciembre Einstein sudaba mucho y constantemente colocaba sus manos sobre los ojos, a modo de visera, para protegerse de la intensa claridad del sol. Los anfitriones le propusieron un programa que comenzaba con una visita oficial al secretario de Estado de Cuba para luego continuar a la Academia de Ciencias, donde recibiría el homenaje de los científicos cubanos. Seguidamente saludaría a la comunidad hebrea residente en la capital y terminaría la jornada matutina almorzando en el hotel Plaza. Él lo aceptó todo con su acostumbrada cortesía y sencillez, pero pidió que antes lo llevaran a algún lugar donde pudiera comprar un sombrero que resguardara su cabeza y sus ojos de aquel intenso sol.
Sus anfitriones eligieron “El Encanto”, la más famosa tienda de ropas de la ciudad, considerada una de las mejores de América Latina. Previamente el Ingeniero Millás había llamado a José Solís, gerente del establecimiento, para prevenirle de la visita y de su intención. Solís recibió al sabio en la entrada del comercio e inmediatamente lo llevó al departamento de sombreros. En aquellos tiempos estaba de moda usarlos y el comerciante buscó en sus almacenes el mejor que tenía: un sombrero de Panamá.
A Einstein le gustó mucho porque era muy cómodo y justo de su medida. Pensó que era fabricado en la isla, pero le llamó la atención oír que era de Panamá y quiso que le aclararan esa duda. Solís le dijo que el sombrero no estaba hecho ni en Cuba, ni en Panamá, sino en Ecuador, en una región llamada Jipijapa donde abunda una palma del mismo nombre cuyas hojas tienen unas características muy especiales y cuyos aborígenes heredan, por generaciones, la habilidad de trenzar y darle forma y tamaño a cada sombrero que requiere de dos a tres meses de intenso trabajo para hacerlo.
Y continuó Solís: este sombrero usted podrá estrujarlo, aplastarlo o pisotearlo y siempre volverá a adquirir su elegante aspecto original. Así es este genuino sombrero de Jipijapa. En cuanto a su otro nombre, se lo pusieron los ingenieros y jefes de obras norteamericanos cuando construían el canal de Panamá a principios del siglo XX. Ellos no sólo lo usaban por su comodidad, frescura, y elegancia, sino también porque al ser tan exclusivo y caro se diferenciaba de las raídas gorras o sucios sombreros que usaban los peones o trabajadores corrientes. Así se reconocía de inmediato, como si fuera la gorra entorchada de un general, la autoridad de los mandamases extranjeros que preferían decir que sus sombreros eran de Panamá a darle crédito a aquella humilde región ecuatoriana que los producía.
Cuando Theodore Roosevelt visitó el canal usó dicho sombrero, lo que aumentó su popularidad. Entre la lista de sus propietarios más famosos se encuentran el primer ministro del Reino Unido, Winston Churchill, el actor estadounidense Humphrey Bogart y el cantante Frank Sinatra.
La ciudad ecuatoriana de Cuenca es el productor principal; sin embargo, el cantón de Montecristi tiene la reputación de producir los sombreros de calidad más fina. Según la tradición, los sombreros de Jipijapa se realizan a partir de las hojas trenzadas de la Carludovica palmata.
Einstein escuchó con atención esos relatos e insistió en pagar por el sombrero. Solís, hombre agradable y convincente, le dijo que era un obsequio de la tienda. Ante la insistencia de Einstein, Solís le expresó entonces que sería un honor para “El Encanto” el tener de recuerdo un retrato suyo hecho en el taller de fotografía de su comercio. El científico lo complació a pesar del poco tiempo disponible.
Gonzalo Lobo era uno de los mejores retratistas de La Habana y firmaba sus fotografías con el pomposo nombre de Van Dyck. Su estudio formaba parte de la gran variedad de departamentos que tenia la tienda para complacer a la exigente burguesía cubana. El fotógrafo con su desenvoltura habitual colocó al sabio delante de un fondo negro para resaltar las canas que cubrían la desordenada cabeza del sabio y captó su expresión característica con la mirada bondadosa e inteligente que caracterizaba su rostro. Así fue la primera visita que realizó el científico en La Habana, acompañado por su esposa Hedwig y sus cicerones cubanos.
Luciendo su fresco sombrero de Jipijapa fue a la Secretaria de Estado y después, escoltado por un ejército de periodistas, asistió al homenaje que le ofrecieron los miembros de la Academia de Ciencias. Saludó a la colonia hebrea de La Habana y concurrió al almuerzo que le brindaron los científicos en el hotel Plaza. Por la tarde se interesó por ver la naturaleza cubana y efectuaron un recorrido en dos autos por la zonas rurales de Santiago de las Vegas, donde pudo admirar las palmas reales y el verdor de la campiña criolla, el recién inaugurado aeropuerto de Rancho Boyeros, la Escuela de aviación Curtis, el embellecido pueblo de Boyeros con su flamante Escuela Técnica Industrial, el Asilo para enfermos mentales de Mazorra y los hermosos jardines del acueducto de Vento. Luego recorrieron el exclusivo reparto de Miramar y las lujosas Sociedades del Havana Yatch Club y el Country Club. No hubo paradas, solo un rápido vistazo por todos aquellos lugares porque a las cinco de la tarde estaba señalada una recepción en la Sociedad Cubana de Ingenieros.
La comitiva no llegó a la hora señalada sino mucho más tarde. Estaban agotados y a Einstein le esperaba, como en la mañana, saludos, abrazos, discursos, brindis y una interminable fila de caza autógrafos. En medio de aquella agobiante aglomeración de invitados y curiosos, de oír palabras cuyo idioma desconocía y de sonreír a todos, se escabulló finalmente hasta el auto donde lo aguardaba su esposa. Prácticamente huyeron para refugiarse en el camarote de su barco. Pero también allí le esperaba una invitación especial que el gobierno le hacía para que descansara en el recién construido Hotel Nacional, el mejor hotel del Caribe. Agradeció el ofrecimiento, pero rehusó aceptarlo.
Al día siguiente, temprano, el director del Observatorio Nacional, ingeniero Millás y su esposa fueron a buscarlo al trasatlántico y como sabían que no le gustaba el protocolo, ni los halagos, le propusieron ir a donde él quisiera. Einstein agradeció la idea y pidió ver los lugares más pobres de la ciudad. Y Millás lo llevó a los solares de la Habana Vieja y los repartos de “Llega y Pon” y “Pan con Timba” nombres que le resultaron muy ocurrentes y simpáticos porque reflejaban el humor de aquellos infortunados, en su mayoría negros.
También conoció el Mercado Único con sus puestos de pescado, frutas y carne fresca, y escuchó a los pregoneros con sus alegres ofertas. Ello le dio una visión real de cómo vivían la mayoría de los cubanos. A su regreso, el barco ya estaba listo para continuar su viaje. Lo esperaba el viejo Solís para regalarle una elegante ampliación del retrato captado por Lobo y también estaban las autoridades, académicos, periodistas y otras personalidades para despedirlo. El barco partió a la una en punto de la tarde y mientras se alejaba, en la cubierta, el sencillo sabio decía adiós a sus amigos habaneros agitando su sombrero de jipijapa.
Al atardecer de ese mismo día, en la vidriera principal de “El Encanto” en la calle Galiano, el decorador dio los retoques finales a una elegante escenografía para homenajear a Einstein. Se apreciaba una gigantesca ampliación del retrato que le había hecho Gonzalo Lobo acompañada de una docena de fotos del reportero grafico Rafael Pegudo que mostraban varios momentos de la visita del científico a la capital. En un rótulo cuidadosamente dibujado se destacaba una frase que Einstein había dicho a la prensa a su llegada a La Habana: “La Ciencia une a los hombres y evita las guerras”
https://almejeiras.wordpress.com/2013/04/23/einstein-estuvo-en-cuba/
|
|
|
|
Rispondi |
Messaggio 1467 di 1558 di questo argomento |
|

 
Estimado lector que rozas una vez más la suave y policromada pluma del Tocororo:
Albert Einstein, Premio Nobel de Física, el científico más importante del siglo XX y posiblemente el segundo de toda la humanidad (el primero es Isaac Newton sin duda alguna) , visitó La Habana el 21 y 22 de diciembre de 1930. Su estancia en la capital se debió a que el Belgenland, barco en que viajaba desde la ciudad holandesa de Amberes, hizo escala en el puerto de La Habana antes de cruzar por el canal de Panamá con destino a la ciudad de San Diego, en la costa norteamericana del Pacífico. En este último lugar lo recibiría Edwin Hubble.
Hubble fue uno de los más importantes astrónomos estadounidenses del siglo XX, famoso principalmente porque en 1929 había demostrado la expansión del universo midiendo el corrimiento hacia el rojo de las galaxias distantes. Hubble es considerado el padre de la cosmología observacional aunque su influencia en astronomía y astrofísica tocó muchos otros campos.
Un poquito de Física: Cuando un tren se acerca a nosotros a gran velocidad haciendo sonar su silbato, notamos una subida en el tono de su sonido (la frecuencia aumenta) pero cuando el tren se aleja de nosotros apreciamos una bajada de ese tono (la frecuencia disminuye). Este fenómeno se conoce como Efecto Doppler y también se produce en el caso de la luz de forma que si miramos hacia una estrella que se acerca a gran velocidad percibimos su luz con un tono azulado pero si se aleja, ese tono sería rojizo. A esto se le llama corrimiento hacia el rojo.
El efecto Doppler puede usarse para medir la velocidad de los coches en la carretera utilizando ondas de radio de onda muy corta. (RADAR).
El propio Einstein, quien creía en un principio en un universo estático, introdujo de forma artificial un término extra a sus ecuaciones, denominado constante cosmológica, para evitar el fenómeno de la expansión. Tras los resultados publicados por Hubble, Einstein se retractó y retiró este término, al que llamó “el mayor error de mi carrera“. Einstein hizo entonces un famoso viaje a Monte Wilson en 1931 para agradecer a Hubble que hubiera sentado las bases de la cosmología moderna.
La alegría de los científicos cubanos de conocer y dialogar con el más notable de los físicos de todo el mundo era tan grande como la preocupación que tenían por la tensa situación social y política que vivía Cuba. Eran tiempos en que el General Gerardo Machado, apoyado por las fuerzas represivas y el apadrinamiento del gobierno yanqui, había prorrogado su mandato presidencial convirtiéndolo en una cruel dictadura. El descontento popular crecía y los estudiantes y revolucionarios se organizaban para enfrentar valientemente a aquel odioso y sangriento régimen. Hacía pocas semanas que en una protesta popular contra el gobierno las balas de la policía habían asesinado a Rafael Trejo, uno de los líderes universitarios más queridos y para colmo, la Universidad acababa de ser clausurada por decreto presidencial.
Los dirigentes de la Academia de Ciencias Médicas, Físicas y Naturales de La Habana y de la Sociedad Geográfica de Cuba trataron de hacer todo lo posible para disimular aquella realidad y darle el tratamiento que correspondía a tan distinguida y singular personalidad. A las ocho de la mañana del día 21 abordaron el barco para darle la bienvenida. También había decenas de periodistas.
Einstein agradeció el saludo de los académicos, dijo algunas palabras a los reporteros y posó para los fotógrafos y camarógrafos cubanos y extranjeros.
Aunque era el mes de diciembre Einstein sudaba mucho y constantemente colocaba sus manos sobre los ojos, a modo de visera, para protegerse de la intensa claridad del sol. Los anfitriones le propusieron un programa que comenzaba con una visita oficial al secretario de Estado de Cuba para luego continuar a la Academia de Ciencias, donde recibiría el homenaje de los científicos cubanos. Seguidamente saludaría a la comunidad hebrea residente en la capital y terminaría la jornada matutina almorzando en el hotel Plaza. Él lo aceptó todo con su acostumbrada cortesía y sencillez, pero pidió que antes lo llevaran a algún lugar donde pudiera comprar un sombrero que resguardara su cabeza y sus ojos de aquel intenso sol.
Sus anfitriones eligieron “El Encanto”, la más famosa tienda de ropas de la ciudad, considerada una de las mejores de América Latina. Previamente el Ingeniero Millás había llamado a José Solís, gerente del establecimiento, para prevenirle de la visita y de su intención. Solís recibió al sabio en la entrada del comercio e inmediatamente lo llevó al departamento de sombreros. En aquellos tiempos estaba de moda usarlos y el comerciante buscó en sus almacenes el mejor que tenía: un sombrero de Panamá.
A Einstein le gustó mucho porque era muy cómodo y justo de su medida. Pensó que era fabricado en la isla, pero le llamó la atención oír que era de Panamá y quiso que le aclararan esa duda. Solís le dijo que el sombrero no estaba hecho ni en Cuba, ni en Panamá, sino en Ecuador, en una región llamada Jipijapa donde abunda una palma del mismo nombre cuyas hojas tienen unas características muy especiales y cuyos aborígenes heredan, por generaciones, la habilidad de trenzar y darle forma y tamaño a cada sombrero que requiere de dos a tres meses de intenso trabajo para hacerlo.
Y continuó Solís: este sombrero usted podrá estrujarlo, aplastarlo o pisotearlo y siempre volverá a adquirir su elegante aspecto original. Así es este genuino sombrero de Jipijapa. En cuanto a su otro nombre, se lo pusieron los ingenieros y jefes de obras norteamericanos cuando construían el canal de Panamá a principios del siglo XX. Ellos no sólo lo usaban por su comodidad, frescura, y elegancia, sino también porque al ser tan exclusivo y caro se diferenciaba de las raídas gorras o sucios sombreros que usaban los peones o trabajadores corrientes. Así se reconocía de inmediato, como si fuera la gorra entorchada de un general, la autoridad de los mandamases extranjeros que preferían decir que sus sombreros eran de Panamá a darle crédito a aquella humilde región ecuatoriana que los producía.
Cuando Theodore Roosevelt visitó el canal usó dicho sombrero, lo que aumentó su popularidad. Entre la lista de sus propietarios más famosos se encuentran el primer ministro del Reino Unido, Winston Churchill, el actor estadounidense Humphrey Bogart y el cantante Frank Sinatra.
La ciudad ecuatoriana de Cuenca es el productor principal; sin embargo, el cantón de Montecristi tiene la reputación de producir los sombreros de calidad más fina. Según la tradición, los sombreros de Jipijapa se realizan a partir de las hojas trenzadas de la Carludovica palmata.
Einstein escuchó con atención esos relatos e insistió en pagar por el sombrero. Solís, hombre agradable y convincente, le dijo que era un obsequio de la tienda. Ante la insistencia de Einstein, Solís le expresó entonces que sería un honor para “El Encanto” el tener de recuerdo un retrato suyo hecho en el taller de fotografía de su comercio. El científico lo complació a pesar del poco tiempo disponible.
Gonzalo Lobo era uno de los mejores retratistas de La Habana y firmaba sus fotografías con el pomposo nombre de Van Dyck. Su estudio formaba parte de la gran variedad de departamentos que tenia la tienda para complacer a la exigente burguesía cubana. El fotógrafo con su desenvoltura habitual colocó al sabio delante de un fondo negro para resaltar las canas que cubrían la desordenada cabeza del sabio y captó su expresión característica con la mirada bondadosa e inteligente que caracterizaba su rostro. Así fue la primera visita que realizó el científico en La Habana, acompañado por su esposa Hedwig y sus cicerones cubanos.
Luciendo su fresco sombrero de Jipijapa fue a la Secretaria de Estado y después, escoltado por un ejército de periodistas, asistió al homenaje que le ofrecieron los miembros de la Academia de Ciencias. Saludó a la colonia hebrea de La Habana y concurrió al almuerzo que le brindaron los científicos en el hotel Plaza. Por la tarde se interesó por ver la naturaleza cubana y efectuaron un recorrido en dos autos por la zonas rurales de Santiago de las Vegas, donde pudo admirar las palmas reales y el verdor de la campiña criolla, el recién inaugurado aeropuerto de Rancho Boyeros, la Escuela de aviación Curtis, el embellecido pueblo de Boyeros con su flamante Escuela Técnica Industrial, el Asilo para enfermos mentales de Mazorra y los hermosos jardines del acueducto de Vento. Luego recorrieron el exclusivo reparto de Miramar y las lujosas Sociedades del Havana Yatch Club y el Country Club. No hubo paradas, solo un rápido vistazo por todos aquellos lugares porque a las cinco de la tarde estaba señalada una recepción en la Sociedad Cubana de Ingenieros.
La comitiva no llegó a la hora señalada sino mucho más tarde. Estaban agotados y a Einstein le esperaba, como en la mañana, saludos, abrazos, discursos, brindis y una interminable fila de caza autógrafos. En medio de aquella agobiante aglomeración de invitados y curiosos, de oír palabras cuyo idioma desconocía y de sonreír a todos, se escabulló finalmente hasta el auto donde lo aguardaba su esposa. Prácticamente huyeron para refugiarse en el camarote de su barco. Pero también allí le esperaba una invitación especial que el gobierno le hacía para que descansara en el recién construido Hotel Nacional, el mejor hotel del Caribe. Agradeció el ofrecimiento, pero rehusó aceptarlo.
Al día siguiente, temprano, el director del Observatorio Nacional, ingeniero Millás y su esposa fueron a buscarlo al trasatlántico y como sabían que no le gustaba el protocolo, ni los halagos, le propusieron ir a donde él quisiera. Einstein agradeció la idea y pidió ver los lugares más pobres de la ciudad. Y Millás lo llevó a los solares de la Habana Vieja y los repartos de “Llega y Pon” y “Pan con Timba” nombres que le resultaron muy ocurrentes y simpáticos porque reflejaban el humor de aquellos infortunados, en su mayoría negros.
También conoció el Mercado Único con sus puestos de pescado, frutas y carne fresca, y escuchó a los pregoneros con sus alegres ofertas. Ello le dio una visión real de cómo vivían la mayoría de los cubanos. A su regreso, el barco ya estaba listo para continuar su viaje. Lo esperaba el viejo Solís para regalarle una elegante ampliación del retrato captado por Lobo y también estaban las autoridades, académicos, periodistas y otras personalidades para despedirlo. El barco partió a la una en punto de la tarde y mientras se alejaba, en la cubierta, el sencillo sabio decía adiós a sus amigos habaneros agitando su sombrero de jipijapa.
Al atardecer de ese mismo día, en la vidriera principal de “El Encanto” en la calle Galiano, el decorador dio los retoques finales a una elegante escenografía para homenajear a Einstein. Se apreciaba una gigantesca ampliación del retrato que le había hecho Gonzalo Lobo acompañada de una docena de fotos del reportero grafico Rafael Pegudo que mostraban varios momentos de la visita del científico a la capital. En un rótulo cuidadosamente dibujado se destacaba una frase que Einstein había dicho a la prensa a su llegada a La Habana: “La Ciencia une a los hombres y evita las guerras”
https://almejeiras.wordpress.com/2013/04/23/einstein-estuvo-en-cuba/
|
|
|
|
Rispondi |
Messaggio 1468 di 1558 di questo argomento |
|
https://lapalabradelbeni.com.bo/municipal/santa-maria-magdalena-dio-muestras-de-hospitalidad/ |
|
|
 Primo Primo
 Precedente
1454 a 1468 de 1558
Successivo Precedente
1454 a 1468 de 1558
Successivo Ultimo
Ultimo
|





.jpg)
















































































































































![Cuba, Isla Mía : ¿Volvería Albert Einstein a escribir "¿Por qué la guerra?" [+ video]](http://4.bp.blogspot.com/-U2MtBxY8tNA/U9hnsqjgtxI/AAAAAAAAmV4/hRoZ9LtfV74/s1600/cita-001.jpg)
![August 6 THE TRANSFIGURATION OF OUR LORD [Feast] MASS PRAYERS AND READINGS. - Catholics Striving For Holiness](https://i2.wp.com/catholicsstrivingforholiness.org/wp-content/uploads/2019/08/AUG.-6-TRANSFIGURATION.jpg)

