Have you ever tried to calculate the value of Pi, the ratio of a circle's circumference to its diameter? Are you wondering how Archimedes first calculated Pi almost 2500 years ago?
When you line up same-size circles in tight rows you see that six circles fit exactly around an inner circle. Or, place six beer cans around a can; they fit exactly. The concept of the Pi calculation is anchored in the eye-opening premise. When we connect the center of each of the seven circles to the center of its neighboring circle, we create six equilateral triangles. Each side of a triangle is equal to the diameter of a circle. Together, the six triangles form a hexagon, a quasi-circle of six sides. The circumference of this six-sided hexagon is thus 6 times a circle's diameter, or 3 times the diameter of the hexagon. For this unfinished, jagged but uniform hexagon circle, the '3' could be said to represent the elementary Pi ratio. This is our starting point in calculating the Pi number. As we refine the circle, doubling the number of sides with each calculation, over and over, we can calculate a more and more precise Pi value. The circle will never be totally round, and the Pi number can thus be calculated to infinity.
For our project, we start with the drawn six-sided hexagon. Since all three sides of the six triangles are equal in length, the sides of the triangle also represent the radius of our rough circle. If we add up the outer sides of all six triangles we get a value of six times the radius, or three times the diameter, a rough approximation of the 3.14 number for Pi that we try to calculate. That is our starting position.
 To get to a refined, more accurate value of Pi, we need to smoothen the circle. For these calculations, we rely on the ingenious Pythagorean theorem that we learned in Grade 6. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
To get to a refined, more accurate value of Pi, we need to smoothen the circle. For these calculations, we rely on the ingenious Pythagorean theorem that we learned in Grade 6. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
With each calculation we cut each side of the quasy circle in half and double the number of sides of the circle. With more sides, the circle becomes rounder and smoother, and the Pi value nudges closer to its infinite value. Although the circle will appear round to the eye, mathematically, the circle will never be perfect, and the Pi can be calculated to its infinity.
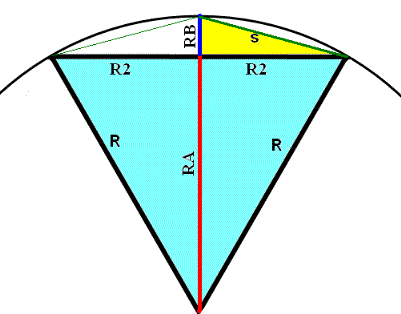
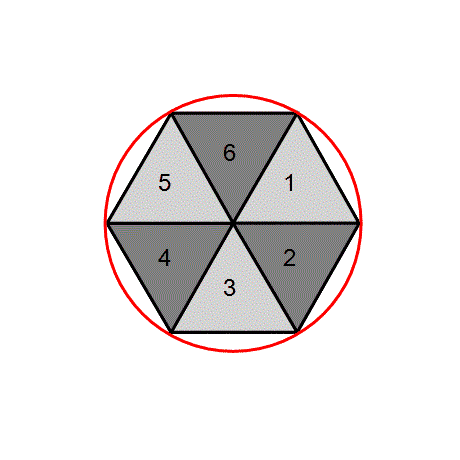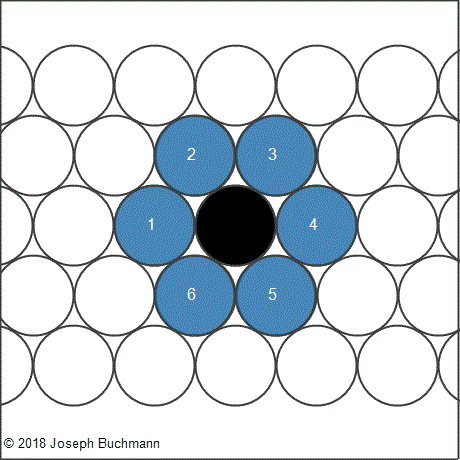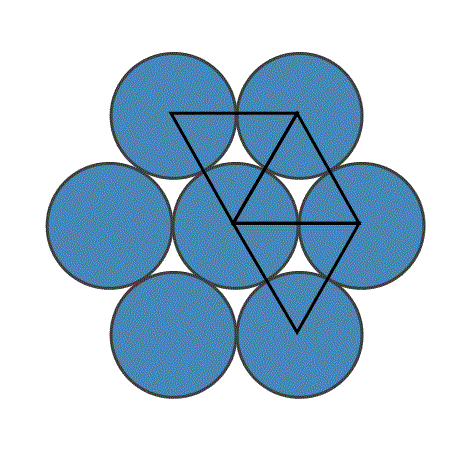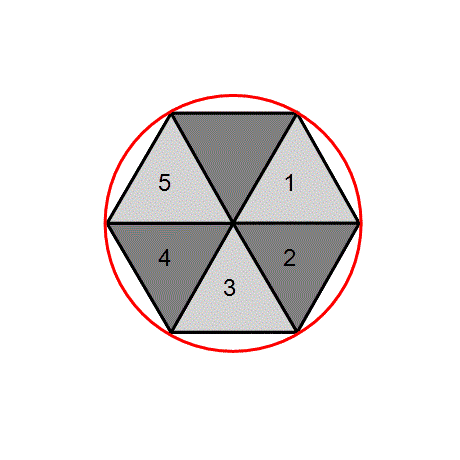
We cut one of the triangles in half and draw a separating line from the center of the circle up to the circumference (combined red RA and blue RB in the image), crossing the upper side of the triangle (R2). That full length of the separating line is equal to the radius, equal in length to each of the original triangle sides. Now, we need to calculate the values of the line section from the center point up to the crossing (red RA) and the line beyond the crossing (blue RB)). Here we need to do our first simple Pythagoras calculation. We know the length of the radius (R) and we know the length of R2 (R2 is of course exactly half of the radius). RA is thus calculated as follows:
RA = Square Root of ((R*R) - (R2 * R2))
Now that we know the value of RA, we calculate the value of RB, by simply deducting the RA from the value of the radius.
 We are now ready to refine the circle line further. The initial six sides will be doubled to 12. With our second Pythagoras calculation, we obtain the hypotenuse of the yellow RB and R2 configuration, shown as a green line (S) in the image. The calculation is as follows:
We are now ready to refine the circle line further. The initial six sides will be doubled to 12. With our second Pythagoras calculation, we obtain the hypotenuse of the yellow RB and R2 configuration, shown as a green line (S) in the image. The calculation is as follows:
S = Square Root of (( R2*R2) + (RB*RB))
With this calculation, we now have 12 equal sections around our circle and the Pi stands much improved at 3.13. Better, but that is not good enough.
And we continue. Using the same steps as above, we cut the sections by half again, and again. The Pi improves to 3.139, then 3.141. Once we get to 20 iterations, we have a near-perfect Pi value of 3.14159265358976. Of course, we write a simple program to do this for us. The sample code is shown below.
We can calculate to infinity; a number is never too small to be cut in half.
Sample code for the Pi calculation in C#:
double radius = 1000;
double sec = 0;
double adjacent = 0;
double opposite = radius / 2;
adjacent = Math.Sqrt((radius * radius) - (opposite * opposite));
sec = Math.Sqrt((opposite * opposite) + ((radius - adjacent) * (radius - adjacent)));
int iterations = 20;
for (int i = 1; i <= iterations; i++)
{
adjacent = Math.Sqrt((radius * radius) - ((sec / 2) * (sec / 2)));
sec = Math.Sqrt(((sec / 2) * (sec / 2)) + ((radius - adjacent) * (radius - adjacent)));
}
double circumference = sec * 6 * (Math.Pow(2, iterations));
double pi = circumference / radius;
MessageBox.Show(pi.ToString());
Each iteration gets closer to the ultimate Pi number, unreachable because the circle is never completely round:
3.10583
3.13263
3.13935
3.14103
3.14145
3.14156
3.14158
...
3.14159265359...
A full circle is expressed as 360 degrees. The common belief is that the number 360 is based on the number of days of the full solar cycle, thus each day representing one degree. The Sumerians and Babylonians of Mesopotamia used the Sexagesimal numbering system (Base-60). Since our quasi-circle has six sides, one could also speculate that Sumerians may have originated the 360 degrees based on the six-sided circle.
https://www.informatik.com/mathfun/# 
