EDT = tiempo solar verdadero - tiempo solar medio
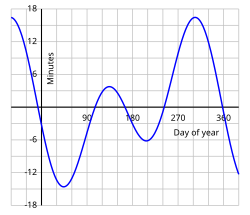
Suele representarse en una gráfica que muestra esa diferencia a lo largo de los dias del año. Según mis cálculos en 2009 es más o menos así:

En la Gráfica 1 la curva negra representa la ecuación del tiempo. La discrepancia entre el tiempo solar verdadero (el del reloj de Sol) y el tiempo solar medio (el del buen reloj convencional) tiene dos causas calculables de forma separada, que llevan aparejadas su ecuación correspondiente:
1- Ecuación de Inclinación de la Eclíptica (EIE). La órbita de la Tierra alrededor del Sol está contenida en un plano inclinado respecto al plano perpendicular al eje de rotación terrestre.
2- Ecuación de Excentricidad de la órbita (EEX). La órbita de la Tierra alrededor del Sol no es circular, sino una elipse con cierta excentricidad.
Estas dos contribuciones, EIE y EEX, que sumadas dan la ecuación del tiempo EDT se muestran también en la Gráfica 1.
(ojo, puede encontrarse en libros o webs la EDT definida con el signo cambiado, y la gráfica por tanto "patas arriba")
Visualizando la EDT con la Esfera Celeste
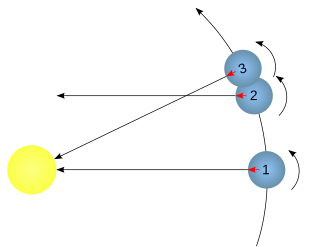
El cálculo de EDT requiere manejar dos sistemas de referencia diferentes. En la Figura 1 se ilustra el punto de vista geocéntrico: la Tierra (pequeña esfera azul claro) en el centro, girando sobre su eje. La esfera celeste (rejilla gris) con sus "estrellas fijas", no mostradas en la Figura 1. Y sobre esa esfera el Sol desplazandose a lo largo del año alrededor de la Tierra sobre la eclíptica (en rojo), en el mismo sentido de la rotación terrestre.Vemos uno de los dos sistemas de referencia a usar en los cálculos, el que llamaré sistema equinoccial. Su centro, el de la Tierra. Su eje Z coincide con el eje de rotación terrestre, y el plano perpendicular al mismo determina sobre la esfera el ecuador celeste (en azul). Este corta a la eclíptica en dos puntos: el punto de Aries, por donde pasa el Sol el día del equinoccio de marzo, y el punto de Libra, por donde pasa el Sol el día del equinoccio de septiembre. El eje X se elige para que pase siempre por el punto de Aries. El eje Y se elige para formar un triedro a derechas. Debido a la precesión de los equinoccios nuestros ejes se mueven muy lentamente respecto a las "estrellas fijas".

La Figura 1 nos ayuda a "ver" la ecuación del tiempo. El tiempo solar medio discurre al ritmo fijo de un buen reloj, y su valor lo determina por definición un punto imaginario, el Sol Ecuatorial Medio, en adelante ECUA, que se mueve uniformemente sobre el ecuador celeste dando una vuelta completa respecto a nuestro sistema equinoccial en un año trópico. Si ajustamos nuestro buen reloj a la hora local del meridiano en que nos encontramos, el reloj debe marcar las 12h del día (solar medio) cuando ECUA culmine sobre nuestro meridiano superior. Hemos marcado este meridiano en gris sobre la superficie terrestre, y también el correspondiente sobre la esfera celeste, pasando por ECUA.
En la situación recogida en la Figura 1, el Sol aún no ha culminado sobre nuestro meridiano cuando justo lo hace ECUA. La Tierra aún tiene que girar hasta que nuestro meridiano "alcance" al Sol, y este culmine, momento en que será el mediodía, las 12h de tiempo solar verdadero. El tiempo solar verdadero va retrasado, a las 12h del tiempo solar medio aún no son las 12h del tiempo solar verdadero, luego EDT es negativa. ¿Por cuantos minutos?
Justo cuando ECUA culmina sobre nosotros, medimos la separación angular sobre el ecuador entre nuestro meridiano, y el meridiano en que se encuentra el Sol, un cuarto del cual se muestra en rojo oscuro en la Figura 1 y sirve para "proyectar" el Sol hasta el punto Sol2 sobre el ecuador celeste.
En ese momento sabemos la diferencia angular entre ECUA y Sol2. La relación entre diferencia angular y temporal se basa en que los 360º corresponden a 24 horas. Por ejemplo, si el Sol va 1º por delante de ECUA, resulta que el tiempo solar verdadero va retrasado 4 minutos horarios respecto al tiempo solar medio. A las 12h de nuestro reloj el Sol culmina en el meridiano cuyo tiempo solar medio local es 12h y 4 minutos (ECUA ya culminó sobre ese meridiano que está 1º al Este del nuestro). Por tanto EDT = -4 minutos.
Esta pesada discusión es la base para el factor de conversión a usar en nuestros cálculos para llegar de cantidades angulares a tiempos expresados en minutos sobre el eje vertical de nuestra gráfica de EDT: 360º o 2π radianes corresponden a 1440 minutos de tiempo solar medio, o a 86400 segundos como el definido en el Sistema Internacional de unidades. También nos indica el curioso e importante hecho de que un adelanto posicional (y angular) del Sol respecto a ECUA, implica un retraso temporal del tiempo solar verdadero respecto al tiempo solar medio.
Dos problemas
Para calcular EDT debemos saber, en función del día del año, donde está ECUA y dónde el Sol, establecer su diferencia angular medida sobre el ecuador, y expresar la misma en términos de minutos de tiempo.ECUA se mueve uniformente sobre el ecuador, pero no así Sol2, la proyección del Sol sobre el ecuador celeste. Hay dos problemas matemáticos a resolver:
PM1- Mediante la geometría esférica, dado un punto sobre la eclíptica, obtener su proyección sobre el ecuador.
PM2- Mediante las leyes de la mecánica determinar cómo se mueve la Tierra alrededor del Sol, y saber así dónde, sobre la esfera celeste, está el Sol visto desde la Tierra.
Resolución de PM1
La resolución de PM1 es "fácil" y además es la única influencia para determinar la ecuación de la inclinación de la eclíptica, EIE.En la Figura 2 tenemos un triangulo esférico determinado por 3 puntos A, B y C.

- A es nuestro origen de medida de arcos en el sistema equinoccial, el punto de Aries.
- AB es un arco sobre la eclíptica, cuya magnitud λ da la longitud eclíptica del punto B.
- AC es un arco sobre el ecuador, cuya magnitud α da la ascensión recta del punto B, igual a la del punto C, que es la proyección de B sobre el ecuador, dado que el arco BC es parte de un meridiano celeste.
- Los lados AB y AC forman un ángulo ε igual a la inclinación (u oblicuidad) de la eclíptica.
Los tres arcos, AB, AC y BC son parte de sendos círculos máximos de la esfera celeste. El punto D sobre el ecuador es tal que determina un arco AD igual en magnitud al arco AB: la ascensión recta de D es igual a la longitud eclíptica de B. En el caso de la Figura 2 se ve claramente que D está a la derecha de C pues AC es menor que AB.
La trigonometría esférica proporciona la siguiente relación entre λ y α para un ε dado:

o esta otra equivalente pero sin la problemática tangente y sus visitas al infinito:

Esta relación se usa tanto en el cálculo directo de EDT, como en el cálculo desglosado de EIE por un lado y EEX por otro.
La Gráfica 2 muestra la diferencia entre λ y α como función de λ:

La periodicidad y el signo de la curva en cada parte de la Gráfica 2 se pueden "seguir" directamente observando la Figura 2. En A es donde más rápidamente se separa la eclíptica del ecuador. Cerca de A el punto B se mueve en parte según el ecuador, y en parte hacia arriba, mientras D sobre el ecuador cubre el mismo arco, AD = AB . La proyección de B sobre el ecuador, el punto C, se retrasa rápidamente: AB = λ > α = AC , es decir, λ-α es positiva y crece.
Pero a 90º desde A la eclíptica llega a su máxima incursión hacia el norte, allí es justamente paralela al ecuador. Alrededor de esa zona un arco dado sobre la eclíptica, al proyectarse sobre el ecuador, se "abre" hasta un arco mayor. Por eso el retraso inicial de C respecto a D va disminuyendo según D (y B) avanzan. Cuando D y B llegan a los 90º desde A, C coincide con D, la diferencia se anula. Tanto sobre la eclíptica como sobre el ecuador se ha completado un cuarto de círculo máximo, λ=α=90º. Se ha completado el primer lóbulo de los cuatro que tiene la Gráfica 2.
Al seguir avanzando dentro aún de la zona de "paralelismo eclíptica-ecuador", C adelanta a D. Pero cuando se va llegando al otro punto de cruce entre eclíptica y ecuador la tendencia vuelve a invertirse, D reduce su distancia a C y le alcanza en el punto opuesto a A, al cubrirse el primer semicírculo, λ=α=180º, y completarse un periodo de la curva mostrada en la Gráfica 2.
Resolución de PM2
En cuanto al otro problema, PM2, tiene una parte física y otra puramente matemática. Su resolución se expresa adecuadamente desde un punto de vista heliocéntrico en un sistema de referencia inercial, que llamaremos sistema orbital, en el que aplicamos las leyes de la mecánica de Newton, con simplificaciones adecuadas. La más drástica, considerar únicamente un sistema de dos cuerpos, el Sol y la Tierra. Entre las consecuencias de tales leyes está que la órbita de la Tierra alrededor del Sol tiene la forma de una elipse (con el Sol en uno de los focos, 1ª ley de Kepler), recorrida con momento angular (y velocidad areolar) constante (2ª ley de Kepler). Esto implica una mayor velocidad lineal cerca del Sol, y menor lejos. La Figura 3 muestra los elementos de la solución del problema, aunque de una forma no realista, pues la excentricidad de la elipse mostrada es mucho mayor que la real de la órbita terrestre.
El Sol es el origen de los ejes del sistema orbital, con el eje de abcisas dirigido hacia el perihelio, que va a ser el origen de medida de ángulos, y con el eje de ordenadas a 90º en el sentido del movimiento de la Tierra. El paso del tiempo va asociado a la posición de un punto M que se mueve uniformemente sobre el círculo rojo, que tiene como diámetro el eje mayor de la elipse. Por tanto el ángulo PCM, llamado anomalía media, M, crece proporcionalmente al tiempo, y completa una vuelta en un año sidéreo, el mismo tiempo en que la Tierra completa su vuelta al Sol visto desde nuestro sistema orbital.
La aplicación de las leyes de la mecánica, además de deducir la forma elíptica de la órbita, conduce a una relación entre la anomalía media M y la llamada anomalía excéntrica E, el ángulo PCE determinado por el punto E de la Figura 3, el centro C de la elipse, y el perihelio P. Resulta que, siendo e la excentricidad de la elipse:

Esta ecuación implícita en E no es resoluble analíticamente, hay que recurrir a aproximaciones o a métodos numéricos para obtener el valor de E para cada M.
¿Y que tiene el punto E de especial? En la Figura 3 se aprecia que la posición del punto E sobre la circunferencia roja está en la misma vertical que pasa por el punto T (la Tierra) sobre la elipse. Hay una relación, deducible de la geometría de la elipse, entre la anomalía excéntrica E, y la llamada anomalía verdadera ν, que es el ángulo PST. Esa relación es :

Por tanto a partir del tiempo t desde el paso por el perihelio se calcula M, a partir de M se calcula E, y a partir de E se calcula ν lo que nos permite saber dónde está la Tierra en ese momento.
La Gráfica 3 muestra la diferencia entre M y ν a lo largo de una órbita completa.

Mientras que M se mueve a velocidad constante sobre el círculo rojo de la Figura 3, la Tierra va más rápida cerca del perihelio y más lenta cerca del afelio. M y T arrancan a la vez al paso por el perihelio, nuestro origen de tiempo y de ángulos, pero enseguida el punto T se "adelanta" al punto M (M < ν). Luego, según se acerca al afelio, T va cada vez más despacio, M a su ritmo constante le va cogiendo y le pilla justo al llegar al afelio (M=180º), y luego le pasa, quedando T rezagado (M > ν). Pero de nuevo al acercarse el perihelio T aumenta su velocidad, va acortando las distancias con M, hasta coincidir de nuevo en el perihelio. Y vuelta a empezar.
Ensamblado de las soluciones
Para obtener EDT solo nos falta un "pequeño detalle", ensamblar el resultado de PM2, obtenido en el sistema de referencia orbital (con origen de ángulos en el perihelio y carácter heliocéntrico), con nuestro sistema equinoccial en el que realizamos la resolución de PM1 (con origen de ángulos en el punto de Aries y carácter geocéntrico). Para ello es esencial conocer la distancia angular entre ambos origenes.Podemos usar los parámetros de la Tierra calculables desde el formulario web disponible en http://aom.giss.nasa.gov/srorbpar.html. Los valores entre 2000 y 2010 son
Parámetros orbitales para la Tierra
Long. del
Año Excentri Oblicuidad Perihelio
(D.C.) cidad (grados) (grados)
------ -------- --------- --------
2000 .016704 23.4398 282.895
2001 .016703 23.4396 282.913
2002 .016703 23.4395 282.930
2003 .016702 23.4394 282.947
2004 .016702 23.4392 282.964
2005 .016702 23.4391 282.981
2006 .016701 23.4390 282.998
2007 .016701 23.4389 283.015
2008 .016700 23.4387 283.033
2009 .016700 23.4386 283.050
2010 .016700 23.4385 283.067

La distancia angular entre perihelio y equinoccio de marzo nos da el desfase entre los dos sistemas empleados, el orbital y el equinoccial. Sólo nos hace falta fijar el tiempo exacto en que se da un evento concreto, por ejemplo el paso del Sol por el equinoccio de marzo. De acuerdo a http://aa.usno.navy.mil/data/docs/EarthSeasons.php en 2009 el equinoccio de marzo es el 20 de marzo a las 11h 44 minutos UT.
Puede calcularse el intervalo temporal entre perihelio y equinoccio de marzo en base a los datos de la anterior página. Pero el momento del perihelio allí reflejado es muy sensible a la interacción Luna-Tierra, y es un poco más adecuado tomar sólo el día del equinoccio como referencia puntual, y usar para la diferencia temporal entre perihelio y equinoccio un tiempo obtenido a partir de la anomalía verdadera en el equinoccio de marzo, deduciendo así la fecha y hora de paso por el perihelio.
Sabiendo de una forma u otra los valores del paso por perihelio y equinoccio de marzo en nuestras unidades de dias del año 2009, se puede calcular EDT directamente.
Para calcular sus componentes, EIE y EEX, además del ya introducido Sol Ecuatorial Medio, ECUA, que se mueve a ritmo constante sobre el ecuador celeste, debemos introducir otro punto ficticio: el Sol Eclíptico Medio, en adelante ECLI.
Visto desde el sistema orbital, ECLI es equivalente al punto M de la anomalía media, se desplaza a ritmo constante (sobre el círculo rojo de la Figura 3), a la velocidad media del Sol, coincidiendo con este en el afelio y en el perihelio, y completando una vuelta en un año sidéreo. Visto desde el sistema equinoccial, ECLI marcha al mismo ritmo constante sobre la eclíptica con que ECUA marcha sobre el ecuador, coincide con ECUA en los dos equinoccios, y completa una vuelta en un año trópico. Al igual que ECUA va asociado al tiempo solar medio, a ECLI se le puede asociar un tiempo solar eclíptico, y poner
EDT = tiempo solar verdadero - tiempo solar medio =
= tiempo solar verdadero - tiempo solar medio + tiempo solar eclíptico - tiempo solar eclíptico =
= (tiempo solar eclíptico - tiempo solar medio ) + ( tiempo solar verdadero - tiempo solar eclíptico) =
= EIE + EEX
Si el Sol tuviese una órbita circular, de excentricidad nula, el Sol coincidiría con ECLI. Por eso la diferencia entre el Sol y ECLI, vista desde el geocéntrico sistema equinoccial, es lo que denominamos ecuación de excentricidad o del centro, EEX. Se debe en efecto a la excentricidad de la órbita, y se anularía si la órbita fuese circular, pero no obstante en el valor y forma de EEX influye también la inclinación de la eclíptica, y el "desfase" entre el paso por el perihelio y por el equinoccio de marzo.
La ecuación de la inclinación de la eclíptica, EIE, corresponde a la diferencia entre las posiciones de ECLI y ECUA. Sería la única a considerar si la órbita fuese circular pues entonces ECLI coincidiría con el Sol.
Los ángulos recorridos por ECUA y ECLI son proporcionales al tiempo, con frecuencias angulares conocidas. En el sistema equinoccial el ángulo de ECUA varía con una frecuencia angular ligada a la duración del año trópico. En el sistema orbital el ángulo de ECLI (la anomalía media) varía con una frecuencia angular ligada a la duración del año sidéreo. E incluso es posible tener en cuenta la lenta precesión de los equinoccios para el paso de las anomalías (media para ECLI, o verdadera para el Sol) en el sistema orbital a las longitudes eclípticas (de ECLI y el Sol) en el sistema equinoccial, paso previo a la obtención de las ascensiones rectas.
En el momento del equinoccio de marzo el Sol pasa por el punto de Aries antes de que lleguen a coincidir allí ECUA y ECLI. Va por delante de ECUA, y EDT es negativa. Además, como se aprecia en la Gráfica 1, EIE aún no se anula, pues tanto ECLI como ECUA aún no han llegado al punto de Aries, donde coincidirán (haciendo EIE=0) un poco después.
En la Figura 5 se recoge gráficamente (de una forma no realista del todo) la situación de todos nuestros puntos de interes unos días después del equinoccio de marzo. EEX es proporcional al ángulo desde Sol2 hasta ECLI2, EIE es proporcional al ángulo desde ECLI2 hasta ECUA, y EDT es proporcional al ángulo desde Sol2 hasta ECUA (suma de los dos anteriores). Los ángulos y sus tiempos son positivos si van en el sentido de giro terrestre y traslación de ECUA, es decir, si los puntos "desde" van posicionalmente por detrás de los puntos "hasta".

El Sol (su proyección Sol2) aún va por delante de ECUA, sigue siendo negativa EDT. También va por delante de ECLI ( Sol2 delante de ECLI2), luego EEX también es negativa (más negativa que EDT). Sin embargo ECLI (ECLI2) va por detrás de ECUA, retrasandose cada vez más en ese primer tramo tras pasar el punto de Aries, lo que implica que EIE es positiva y creciendo. La variación de las curvas de la Gráfica 1 se pueden relacionar así con el movimiento del Sol, ECUA y ECLI, ilustrado en la Figura 5.
Herramientas
Para confeccionar esta "pequeña" entrada del blog me he servido de varias herramientas a las que deseo presentar mis agradecimientos:♦ Octave como herramienta para calcular y presentar las Gráficas
♦ Winplot como herramienta de construcción de las Figuras
♦ Lightscreen como capturador de pantalla para obtener los ficheros png de gráficas y figuras
♦ innumerables sitios web, como wikipedia Es, wikipedia En, giss.nasa, usno, jpl.nasa, DRAE, editor online de ecuaciones latex, ...
♦ el magnífico Curso de Astronomía General, editorial Mir, de P.I. Bakulin, E. V. Kononóvich y V.I. Moroz, traducido del ruso por Virgilio Llanos Mas, donde se describen nuestros imaginarios soles (ecuatorial y eclíptico) medios, aunque el convenio para la ecuación del tiempo tiene el signo cambiado respecto al elegido aquí.
En este enlace pueden encontrarse con la extensión .txt los ficheros de Octave para generar las Gráficas, que hacen uso de ecuTiempo.txt, con las funciones Octave que implementan la solución de los dos problemas, así como imagenes .png de las Gráficas y Figuras. No hay ninguna garantía de que algo de todo esto sea correcto y exento de errores (Disclaimer total :-), pero me ha entretenido lo suyo.