|
Reply |
Message 1 of 7 on the subject |
|
Phi and Mathematics
Note: nx means n raised to the x power. Some browsers may not display exponents as superscripts or raised characters.
Deriving Phi mathematically

Phi can be derived by solving the equation:
n2 - n1 - n0 = 0,
which is the same as:
n2 - n - 1 = 0
This equation can be rewritten as:
n2 = n + 1 and 1 / n = n – 1
The solution to the equation is the square root of 5 plus 1 divided by 2:
( 5½ + 1 ) / 2 = 1.6180339… = Phi
This, of course, results in two properties unique to phi:
- If you square phi, you get a number exactly 1 greater than phi: 2.61804…
Phi2 = Phi + 1
- If you divide phi into 1, you get a number exactly 1 less than phi: 0.61804…:
1 / Phi = Phi – 1
Phi, curiously, can also be expressed all in fives as:
5 ^ .5 * .5 + .5 = Phi
This provides a great, simple way to compute phi on a calculator or spreadsheet!
Determining the nth number of the Fibonacci series
You can use phi to compute the nth number in the Fibonacci series (fn):
fn = Phi n / 5½
As an example, the 40th number in the Fibonacci series is 102,334,155, which can be computed as:
f40 = Phi 40 / 5½ = 102,334,155
This method actually provides an estimate which always rounds to the correct Fibonacci number.
You can compute any number of the Fibonacci series (fn) exactly with a little more work:
fn = [ Phi n - (-Phi)-n ] / (2Phi-1)
Note: 2Phi-1 = 5½= The square root of 5
Determining Phi with Trigonometry and Limits
Phi can be related to Pi through trigonometric functions:

Phi can be related to e, the base of natural logs,
through the inverse hyperbolic sine function:
Phi = e ^ asinh(.5)
It can be expressed as a limit:

or

Other unusual phi relationships
There are many unusual relationships in the Fibonacci series. For example, for any three numbers in the series Phi(n-1), Phi(n) and Phi(n+1), the following relationship exists:
Phi(n-1) * Phi(n+1) = Phi(n)2 - (-1)n
( e.g., 3*8 = 52-1 or 5*13=82+1 )
Here’s another:
Every nth Fibonacci number is a multiple of Phi(n),
where Phi(n) is the nth number of the Fibonacci sequence.
Given 0, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765
(Every 4th number, e.g., 3, 21, 144 and 987, are all multiples of Phi(4), which is 3)
(Every 5th number, e.g., 5, 55, 610, and 6765, are all multiples of Phi(5), which is 5)
And another:
The first perfect square in the Fibonacci series, 144,
is number 12 in the series and its square root is 12!
0, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
or, if not starting with 0:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
|
|
|
 First
First
 Previous
2 to 7 of 7
Next
Previous
2 to 7 of 7
Next
 Last
Last

|
|
Reply |
Message 2 of 7 on the subject |
|
Golden ratio
From Wikipedia, the free encyclopedia

Line segments in the golden ratio

A golden rectangle with longer side a and shorter side b, when placed adjacent to a square with sides of length a, will produce a similar golden rectangle with longer side a + b and shorter side a. This illustrates the relationship 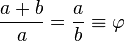 .
The golden ratio ( ) is also called the golden section (Latin: sectio aurea) or golden mean.[1][2][3] Other names include extreme and mean ratio,[4] medial section, divine proportion, divine section (Latin: sectio divina), golden proportion, golden cut,[5] golden number, and mean of Phidias.[6][7][8] ) is also called the golden section (Latin: sectio aurea) or golden mean.[1][2][3] Other names include extreme and mean ratio,[4] medial section, divine proportion, divine section (Latin: sectio divina), golden proportion, golden cut,[5] golden number, and mean of Phidias.[6][7][8]
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The figure on the right illustrates the geometric relationship. Expressed algebraically:
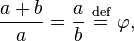
where the Greek letter phi ( ) represents the golden ratio. Its value is: ) represents the golden ratio. Its value is:
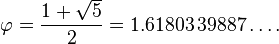 [9] [9]
Many 20th century artists and architects have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be aesthetically pleasing (see Applications and observations below). Mathematicians since Euclid have studied the properties of the golden ratio, including its appearance in the dimensions of a regular pentagon and in a golden rectangle, which can be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has also been used to analyze the proportions of natural objects as well as man-made systems such as financial markets, in some cases based on dubious fits to data.[10]
[edit] Calculation
Two quantities a and b are said to be in the golden ratio φ if:
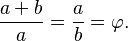
One method for finding the value of φ is to start with the left fraction. Through simplifying the fraction and substituting in b/a = 1/φ,
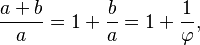
it is shown that
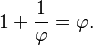
Multiplying by φ gives
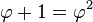
which can be rearranged to
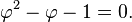
Using the quadratic formula, the only positive solution is
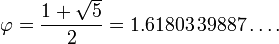
[edit] History

Mathematician Mark Barr proposed using the first letter in the name of Greek sculptor Phidias, phi, to symbolize the golden ratio. Usually, the lowercase form (φ) is used. Sometimes, the uppercase form (Φ) is used for the reciprocal of the golden ratio, 1/φ. [11]
The golden ratio has fascinated Western intellectuals of diverse interests for at least 2,400 years. According to Mario Livio:
Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. But the fascination with the Golden Ratio is not confined just to mathematicians. Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics. [12]
Ancient Greek mathematicians first studied what we now call the golden ratio because of its frequent appearance in geometry. The division of a line into "extreme and mean ratio" (the golden section) is important in the geometry of regular pentagrams and pentagons. The Greeks usually attributed discovery of this concept to Pythagoras or his followers. The regular pentagram, which has a regular pentagon inscribed within it, was the Pythagoreans' symbol.
Euclid's Elements (Greek: Στοιχεῖα) provides the first known written definition of what is now called the golden ratio: "A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less."[4] Euclid explains a construction for cutting (sectioning) a line "in extreme and mean ratio", i.e. the golden ratio.[13] Throughout the Elements, several propositions (theorems in modern terminology) and their proofs employ the golden ratio.[14] Some of these propositions show that the golden ratio is an irrational number.
The name "extreme and mean ratio" was the principal term used from the 3rd century BC[4] until about the 18th century.
The modern history of the golden ratio starts with Luca Pacioli's De divina proportione of 1509, which captured the imagination[citation needed] of artists, architects, scientists, and mystics with the properties, mathematical and otherwise, of the golden ratio.

Michael Maestlin, first to publish a decimal approximation of the golden ratio, in 1597.
The first known approximation of the (inverse) golden ratio by a decimal fraction, stated as "about 0.6180340," was written in 1597 by Michael Maestlin of the University of Tübingen in a letter to his former student Johannes Kepler.[15]
Since the twentieth century, the golden ratio has been represented by the Greek letter Φ or φ (phi, after Phidias, a sculptor who is said to have employed it) or less commonly by τ (tau, the first letter of the ancient Greek root τομή—meaning cut).[1][16]
[edit] Timeline
Timeline according to Priya Hemenway.[17]
- Phidias (490–430 BC) made the Parthenon statues that seem to embody the golden ratio.
- Plato (427–347 BC), in his Timaeus, describes five possible regular solids (the Platonic solids: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron), some of which are related to the golden ratio.[18]
- Euclid (c. 325–c. 265 BC), in his Elements, gave the first recorded definition of the golden ratio, which he called, as translated into English, "extreme and mean ratio" (Greek: ἄκρος καὶ μέσος λόγος).[4]
- Fibonacci (1170–1250) mentioned the numerical series now named after him in his Liber Abaci; the ratio of sequential elements of the Fibonacci sequence approaches the golden ratio asymptotically.
- Luca Pacioli (1445–1517) defines the golden ratio as the "divine proportion" in his Divina Proportione.
- Michael Maestlin (1550–1631) publishes the first known approximation of the (inverse) golden ratio as a decimal fraction.
- Johannes Kepler (1571–1630) proves that the golden ratio is the limit of the ratio of consecutive Fibonacci numbers,[19] and describes the golden ratio as a "precious jewel": "Geometry has two great treasures: one is the Theorem of Pythagoras, and the other the division of a line into extreme and mean ratio; the first we may compare to a measure of gold, the second we may name a precious jewel." These two treasures are combined in the Kepler triangle.
- Charles Bonnet (1720–1793) points out that in the spiral phyllotaxis of plants going clockwise and counter-clockwise were frequently two successive Fibonacci series.
- Martin Ohm (1792–1872) is believed to be the first to use the term goldener Schnitt (golden section) to describe this ratio, in 1835.[20]
- Édouard Lucas (1842–1891) gives the numerical sequence now known as the Fibonacci sequence its present name.
- Mark Barr (20th century) suggests the Greek letter phi (φ), the initial letter of Greek sculptor Phidias's name, as a symbol for the golden ratio.[21]
- Roger Penrose (b.1931) discovered a symmetrical pattern that uses the golden ratio in the field of aperiodic tilings, which led to new discoveries about quasicrystals.
|
|
|
|
Reply |
Message 3 of 7 on the subject |
|
|
|
|
Reply |
Message 4 of 7 on the subject |
|
| Educativo |
| |
| Matemática |
| Artículo #3. La Matemática en la Geometría Sustentable |
| |
| ®Todos los derechos reservados. Autor del documento: Arturo Ponce de León para Psicogeometría México. Colaboración: Ninón Fregoso.Se autoriza la reproducción del material contenido en este sitio siempre y cuando se cite la fuente y se respete la integridad del texto. |
| |
|
¿Qué es el número áureo o phi?
Phi (1.618033988749895... ), pronunciado “fi”, es un numero irracional tal como pi (3.14159265358979... ), pero con muchas características matemáticas inusuales. Phi es la base de la proporción dorada. La razón o proporción determinada por Phi (1.618...) era conocida, por los griegos, como la “Sección Dorada” y, por los artistas del Renacimiento, como la “Proporción Divina”. También se le conoce como la razón dorada o la proporción áurea.
Phi, como pi, es una razón definida por una construcción geométrica. Esta última es la relación de la circunferencia de un círculo respecto a su diámetro y phi es la proporción de los segmentos de una línea que resultan cuando una línea es dividida de una forma única y especial, que explicaremos a continuación.
 | La línea es dividida para que la proporción de la longitud de la línea entera (A) respecto a la longitud del segmento de la línea mayor (B) sea igual que la proporción de la longitud del segmento de la línea mayor (B) a la longitud del segmento de la línea menor (C) |
Esto significa que A es 1.618... veces B, y B es 1.618… veces C. Recíprocamente, C es 0.618... de B y B es 0.618... de A. Phi, escrito con mayúscula, es 1.6180339887..., mientras que phi con minúscula es 0.6180339887, el recíproco de Phi o Phi menos 1.
Lo que hace a phi incluso más inusual es que puede derivarse de muchas formas y ser encontrado, proporcionalmente, en el Universo. Phi puede ser derivado por la serie numérica descubierta por Leonardo Fibonacci, por las matemáticas y por la Geometría.
Phi y la serie de Fibonacci
Leonardo Fibonacci, por herencia del mundo árabe, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Por lo tanto, la serie queda construida de la siguiente manera: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .
La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618..). Así es como si dividimos 5 entre 3 obtenemos 1.666..., y 8 entre 5 da 1.60. En la medida en la que vayamos más lejos del 0 (punto de inicio de la secuencia), más nos acercamos al valor de phi.
La tabla de abajo nos muestra cómo las proporciones de números sucesivos en la serie Fibonacci se aproxima a phi.
Se puede computar cualquier número de la serie Fibonacci fácilmente. Se debe usar phi para saber cualquier número (n) de la serie Fibonacci (f)
fn = Fn / 51⁄2
Phi puede derivarse matemáticamente resolviendo la ecuación:
n2 - n1 - n0 = 0, que es lo mismo que n2 - n - 1 = 0
Esta ecuación la reescribimos y nos queda así:
n2 = n + 1 y 1 / n = n - 1
La solución a la ecuación es la raíz cuadrada de 5 más 1 dividido entre 2
( 51⁄2 + 1 ) / 2 = 1.6180339... = F
Esto resulta en dos propiedades únicas de phi:
Si elevas al cuadrado a phi, obtienes exactamente 1 número más que phi: 2.6180...
F2 = F + 1
Si divides a phi entre 1, obtienes exactamente 1 número menos que phi: 0.6180...:
1 / F = F - 1
Phi, curiosamente, puede ser expresado en cinco: 5 ^ .5 * .5 + .5 = F
Puedes usar phi para computar un número n en la serie Fibonacci (fn): fn = Fn / 51⁄2
Como por ejemplo, el número 40 de la serie Fibonacci es 102, 334, 155, que puede expresarse
f40 = F40 / 51⁄2 = 102,334,155
Este método en realidad nos provee un estimado que siempre está cerca del número correcto Fibonacci.
Funciones trigonométricas
Phi también puede ser relacionada a pi por funciones trigonométricas.

Phi puede ser relacionado con “e”, base de los logaritmos naturales, por el inverso hiperbólico de la función seno: F = e ^ asinh(.5)
Puede ser expresado como un límite, dándonos una idea de su capacidad de auto recurrencia:
|


| Es importante mencionar que phi es puede ser una razón matemática, una razón aritmética o una razón geométrica.
Pero, ante todo, ¿qué entendemos por razones matemáticas? |
Razones matemáticas
En matemáticas, el termino “razón” significa una relación específica de un número con respecto a otro, como el punto medio respecto a dos extremos,
Razón aritmética
En la imagen se muestra que la razón aritmética de 2 y 8 es 5, porque 5 está a la misma distancia entre ambos, si sumamos sus distancias:
2 + 3 = 5 y 5 + 3 = 8

Para la razón aritmética (b) de 2 números (a) y (c): b = ( a + c ) / 2
La razón aritmética, entonces, es el simple promedio (suma) entre dos números
Razón geométrica
La razón geométrica es similar, pero está basada en múltiplos comunes que relacionan su razón a los otros dos números. Por ejemplo, la razón geométrica de 1 y 9 es 3, porque 3 está en la misma distancia de ambos si se multiplica su distancia:
1*3 = 3 y 3 * 3 = 9

Así 1 es a 3 como 3 es a 9.
Para la razón geométrica (b) de dos números (a) y (c), b es la raíz cuadrada de a por c.
Razón aurea
La razón dorada es una razón geométrica muy específica. En la razón geométrica de arriba, vimos las longitudes siguientes de segmentos de línea en una línea de números: 1,3,9.
Aquí, 1 x 3 = 3 y 3 x 3 = 9, pero 3 + 3 = 6, no 9. La razón dorada impone el requerimiento adicional de que los dos segmentos que definen la razón también deben sumarse a la longitud del segmento completo de la línea:

Esto solamente ocurre en un punto, que como podemos ver arriba es sólo un poco menos que 5/8, o 0.625. El punto exacto de la razón dorada es 0.6180339887..., donde:
A es a B como B es a C, y B + C = A

El número 5 esta intrínsecamente relacionado con phi con la serie Fibonacci.
Phi puede ser derivado de varias formulas basadas en el número 5. La más tradicional, basada en la construcción geométrica de phi, es: Phi = (v5+1)/2
Esta formula también puede ser expresada en cincos, como sigue: F = 5 ^ .5 * .5 + .5
Otra fórmula para phi basada enteramente en cincos, es: F= v((5+v5)/(5-v5))
Los términos de la representación de arriba de phi también pueden ser expresados de otra forma que involucra al 5: (5+v5) x (5-v5) = 5 + 5 + 5 + 5
Pentágono
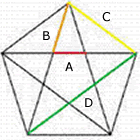 |
Tomemos un pentágono con cinco lados iguales y conectemos todos sus puntos para formar una estrella de cinco puntas. Las razones de la longitud de los segmentos de línea resultantes están todos basados en phi.
En la imagen, notamos que A:B como B:C como C:D =0.618033 (el inverso de phi)
|
Se puede computar un número (n) de la serie Fibonacci (fn) usando phi y la raíz de 5: fn = Fn / 51⁄2
El 5 es también el quinto número de Fibonacci, en 0,1,1,2,3,5
El 5 aparece en cuerpo humano, que tiene proporciones basadas en phi. 5 extensiones del torso; 1 cabeza, 2 brazos, 2 piernas. 5 extensiones de cada brazo y piernas, en 5 dedos cada una. 5 aperturas en la cara y 5 sentidos: vista, oído, gusto, tacto, olfato.
Espiral áurea (espiral dorada)
|

Espiral Dorada creando Punto de Implosión en la Tierra
| Si sumamos los cuadrados de cualquier serie de los números Fibonacci, van a igualar el último número Fibonacci usado en la serie por el siguiente número Fibonacci.
Esta propiedad se ve en la espiral dorada, que se encuentra desde la concha del molusco Nautilus hasta en las galaxias:
12 + 12 + 22 + 32 + 52 = 5 x 8
Entonces, 12 + 12 + . . . + F(n)2 = F(n) x F(n+1) |
Nota: la espiral basada en la serie de Fibonacci es ligeramente diferente a la espiral perfecta generada por phi debido a las aproximaciones en la serie a phi. (1, 1, 2, 3, 5, 8 y 13 producen proporciones de 1, 2, 1.5, 1.67, 1.6 y 1.625)
Las espirales alternas en las plantas ocurren en los números Fibonacci. Las plantas ilustran la serie de Fibonacci en el número de sus hojas, en el arreglo de las hojas alrededor del tallo y en la posición de las hojas, las secciones y las semillas. En la imagen podemos ver el centro de un girasol que ilustra este principio como 55 espirales en el sentido de las manecillas del reloj y 89 en contra.
Podemos apreciar, en esta confiera, 8 espirales girando hacia un lado y 13 girando hacia el lado contrario. 8 y 13 son dos de los números de la secuencia Fibonacci. El principio de la creación de la gravedad y de la vida.
| Trabajo de Dan Winter al respecto aquí |  |
| | |
| La concha del Nautilus y la espiral dorada

Recomendamos visitar nuestra sección de Arte.
|  |
| | |
| Observemos ahora las espirales áureas en esta imagen. ¿Podemos ver cuántas giran hacia la derecha y cuántas hacia la izquierda? ¿Serán siempre múltiplos y submúltiplos de la secuencia numérica Fibonacci? |  |
|
|
|
|
|
Reply |
Message 5 of 7 on the subject |
|
Archimedes` constant PI and the Golden Section
PI is one of those numbers that cannot be evaluated exactly as a decimal - it is in that class of numbers called irrationals. The hunt for PI began in Egypt and in Babylon about two thousand years before Christ. The Egyptians obtained the value (4/3)4=3.160493827 and the Babylonians the value 3 1/8=3.125 for PI.About the same time, the Indians used the square root of 10 for PI.
In the 3rd century B.C. Archimedes considered inscribed and circumscribed polygons of 96 sides and deduced that 3 + 10/71 < PI < 3 + 1/7 .
|
|
Archimedes was born about 287 BC in Syracuse, Sicily. At the time Syracuse was an independent Greek city-state with a 500-year history. Probably studied in Alexandria, Egypt, under the followers of Euclid. Archimedes' father was Phidias, an astronomer . Archimedes' fields of science were : hydrostatics, static mechanics, pycnometry (the measurement of the volume or density of an object). He is called the "father of integral calculus." The order in which Archimedes wrote his works is not known for certain. The works of Archimedes which have survived are as follows: On plane equilibriums (two books), Quadrature of the parabola, On the sphere and cylinder (two books), On spirals, On conoids and spheroids, On floating bodies (two books), Measurement of a circle, and The Sandreckoner. Archimedes generally regarded as the greatest mathematician and scientist of antiquity and one of the three greatest mathematicians of all time (together with Isaac Newton (English 1643-1727) and Carl Friedrich Gauss (German 1777-1855)).
|
It is known that the area enclosed by a circle of radius 1 is:
while its circumference is:
Archimedes`constant PI has many infinite series, infinite product and continued fraction representations. As a continued fraction, PI can be written as :
This form of continued fraction was found in 1665. by William Brouncker.
Surprisingly there are several formulae that use Root-5 and Golden Section ( Phi, phi ) to compute PI.
The Golden Section occurs in Geometry and Trigonometry. So :
where continued fraction of Phi is:
Now we return to using Golden Section and Root-5 to compute PI:
The two most famous numbers in the history of mathematics, phi and pi , are exactly related to each by a several formulae, even though both are irrational numbers.For example:
Ed Oberg and Jay A. Johnson have developed a unique expression for the PI-Phi product as a function of the number 2 and an expression they call "The Biwabik Sum," a function of Phi, the set of all odd numbers and the set of all Fibonacci numbers, as follows:
| p Phi = 22 {1 |
+ [ (2/3) / (F1+F2Phi) + (1/5) / (F3+F4Phi) - (1/7) / (F5+F6Phi) ] |
| |
- [ (2/9) / (F7+F8Phi) + (1/11) / (F9+F10Phi) - (1/13) / (F11+F12Phi) ] |
| |
+ [ (2/15) / (F13+F14Phi) + (1/17) / (F15+F16Phi) - (1/19) / (F17+F18Phi) ] |
| |
- … } |
| |
= 5.083203692.... |
Now, we return to using the golden secion number phi to compute Archimedes`constant PI. Well-known trigonometry`s two-angle tanges formula is:
Putting
where the next relation is valid,
we get
and we calculate the value of t:
In case x=1 we found the following formula styled the Oberg Formula:
The Oberg Formula is the connection between Archimedes`constant PI and the golden section.
http://milan.milanovic.org/math/english/pi/pi.html |
|
|
|
Reply |
Message 6 of 7 on the subject |
|
The Lost Symbol
The Search for Eternity
Throughout the years, the finest of human minds have tried to spread truths or knowledge that they had discovered, and challenged the common perceptions of their times. A large portion of those people were tortured, shunned, or paid with their lives.
There is another way to bring knowledge to the enlightened person. The coding of knowledge in symbols has been one of the most common ways in human history. Another interesting way is conveying messages through books. Books are a more comfortable means of “digestion” by society, especially if the fundamental truth is obscured by a tale of fantasy or science fiction. Examples of this are “Gulliver's Travels” by Jonathan Swift which was actually a profound criticism of society, or “The Master and Margarita” by Mikhail Bulgakov which protested against Stalin and the communist regime.
The Divine Reflection
Assimilating criticism or truth that is hard to digest in a book is more comfortable because the reader receives the message through a filter of a fictional plot. Instead of slamming the truth in the reader's face, the message is transferred slowly to the enlightened reader.
The Lost Symbol book
This form of symbolic coding or encryption existed and continue to do so throughout human history. A surprising source of this type of encryption can be found in Dan Brown's recent novel “The Lost Symbol”. In this novel, written in the form of a popular thriller, an important message is conveyed, a message that has been encrypted throughout the generations and has resurfaced throughout time. It is the human search for the divine and the eternal. From the dawn of time, mankind looked at itself and had seen the entropy, the extinction, and the change. The human fear of the upcoming end, had lead mankind to seek the eternal. The search had lead to several interesting phenomena.
The first phenomenon is religion, which provided answers and a path for the masses. The fear of the end was transformed to a promise of eternal life in paradise for the believer after his death. Ancient civilizations such as the Maya and the ancient Egyptians dealt with religious rituals and preparations for the after life on a daily basis. Absurdly, the search for the truth lead to cynical exploitation of the masses and the use of “mediators” that "linked" those higher powers to humanity.
This cynical cycle of exploitation of the masses by threats and fear lead the discoverers of the truth to encrypt the truth about the nature of reality and the true nature and ability of man. The truth was coded in artwork, architectural monuments, and philosophical and religious writings.
The secrets of ancients
In order to discover the secret of the ancients, we must go back to the ancient world. The ancients observed the complex universe around them with wonder. They discovered patterns and periodical cycles that repeat themselves in nature. Wonderful interactions and organized structures that suggested a mysterious and amazing presence of laws and set patterns in the universe.
Ancient Philosophers and the Golden Ratio
Discovery of geometric relations in the universe lead the lovers of truth, the ancient philosophers (the word philosophy is derived from two Greek words philo and sophy meaning love of truth) to the discovery of the “Golden Ratio”. It is a geometric ratio that exists in countless patterns and structures in the universe.
 Figure 1 The Golden Ratio
The Golden Ratio or Golden Section is a ratio that is formed when a line is divided in this form (Figure 1) so that AB/AC=AC/CB. Namely that the ratio between AB and AC is equal to the ratio between the ratio between AC and CB. This proportion shows us that the ratio between all of the line AB to it bigger section AC is equal to the ratio between AC and the smaller section BC. When this is calculated mathematically the number 1.61803... is attained. This number is known as Phi (φ) and this is it's mathematical equation (Figure 2). The Greek symbol of Phi is parallel to the sound “PH” in English and is used to represent the proportion of the Golden Ratio. The name Phi is derived from the name of the ancient Greek sculptor Phidias who was also a mathematician and built the Parthenon and the sculptures there based on the Golden Ratio. One of the surprising things regarding the Golden Ratio is the geometric law that represents the idea that the Micro and the Macro are the same. In essence, the Golden Ratio reveals to us that the laws that govern the motion of the starts and galaxies are the same laws that make up the human body. As the ancients dived deeper into the law they discovered more and more mysterious facts. They discovered that the law reflects the mysterious relativity between man and universe. The ancients actually discovered that through the laws of the Golden Ratio, they could unveil the secrets of the universe and find eternity.
A Golden Symbol of Harmony and Tranquility
The first of the ancient mathematicians laid the foundation for the search for eternity. Euclid, in his first mathematical book “ Elements” which Albert Einstein called “The Devine Book”, laid the foundations for modern geometry. Along with it came Plato and the five perfect solids which hold the secrets of the Golden Ratio.
The Magical Mystery Tour
Pythagoras (considered the father of philosophy) and his disciples claimed that the entire universe leans on mathematical laws. They believed that in its deepest level, reality is mathematical in nature, and that philosophy is a genuine tool for spiritual understanding. Moreover they believed that the human spirit can experience unification with the divine and that certain symbols have real mystical meanings. Over time this knowledge was forgotten and “rediscovered” in the Renaissance by men like Luca Pacioli, Leonardo Pisano Fibonacci, and more.
The places where this knowledge was encrypted are surprising.
In the bible the Golden Ratio appears in the book of Genesis in the story of Noah's ark, where God instructs Noah to build an ark:
"13: And God said unto Noah, The end of all flesh is come before me; for the earth is filled with violence through them; and, behold, I will destroy them with the earth.
14: Make thee an ark of gopher wood; rooms shalt thou make in the ark, and shalt pitch it within and without with pitch.
15: And this is the fashion which thou shalt make it of: The length of the ark shall be three hundred cubits, the breadth of it fifty cubits, and the height of it thirty cubits.” (King James Version).
Also in the Book of Exodus when God commands Moses to build the Ark of the Covenant.
“10: And they shall make an ark of shittim wood: two cubits and a half shall be the length thereof, and a cubit and a half the breadth thereof, and a cubit and a half the height thereof.
11: And thou shalt overlay it with pure gold, within and without shalt thou overlay it, and shalt make upon it a crown of gold round about.” (King James Version).
Division of the measurements in both cases gives the number 1.666666....namely the Golden Ratio in an almost perfect manner. In the case of Noah's Ark, the numbers 3 and 5 are part of the Fibonacci series which is directly tied to the Golden Ratio and exists in countless places in nature.
Actually the story of the Ark of the Covenant holds several ideas in it. The use of the Golden Ratio in the Ark of the Covenant represents the gate to the secrets of creation and divinity.
The Monad symbol
The Ancient Alchemy symbol for Gold happens to be the ancient philosophical symbol for unity and the beginning of creation. This is the symbol of the Monad. The use of this symbol ,the circumpunct, was used by the Greek philosophers and Pythagoras to represent the point of the beginning of creation. From this symbol one may evolve towards the additional rules of creation including the Golden Ratio.
[Figure 4]
The Monad symbolizes the secret of creation and contains the idea of cosmic consciousness which experiences itself and learns from itself by observation and experience of the micro and the macro, and vice versa. The ancient alchemists used this symbol to represent Gold because Gold represents the divine and the eternal, since Gold is not subject to annihilation and entropy.
A Golden Symbol of Harmony and Tranquility
The measurements of the Temple in Jerusalem and other hidden proportions claimed to be encrypted in the Bible kept many busy over the years. One of the researchers who tried to discover additional cosmic secrets from the structure of the Temple in Jerusalem was non other then Isaac Newton, the father of modern physics, who became engrossed in the Bible and in ancient Jewish mystical writings in order to find more encryptions of the secrets of the universe.
The Lost Secret
The fact that many philosophers delved into esoteric and mystical writing raises two questions. The first being -do these ancient writings contain secret encrypted truths? The second: if so, what is this truth?
The symbol of the Monad is a basic symbol, and from it another symbol is derived – the Tetractys.
When I observed sacred numbers in Jewish tradition such as 5, 13, 26, and 72 I discovered them surprisingly in a consistent form in artworks of the great masters of the Renaissance and in the geometric structures the greek philosophers studied.
If we take the most important symbol of the Pythagoreans – the Tetractys, we will find a surprising discovery. The Tetractys was to the Pythagoreans the symbol and the diagram of the entire universe. The meaning of the word Tetractys in Greek is “Fourfold”. The symbol of the Tetractys was so important to the Pythagorans that they used it as their oath. "By him that gave to our generation the Tetractys, which contains the fount and root of eternal nature…..".

Now notice this. In the Bible the name of God is written as YAWH (יהוה) and the letters represent the cycle of time and the periodical motion of the universe. This name is comprised of the words “Was” (היה), “Is” (הווה), and “Will be” (יהיה). The name simply represents a state of "being" or "existence".In the Jewish tradition there are the 72 sacred names of God– these are 72 combinations of three letters that are created by sectioning the middle verse of the Bible in a certain way. According to Jewish tradition, with these combinations – creation was made. If you take the name of God in Hebrew (יהוה) and place it in the order of the letters in the Tetractys, you will get the number 72.
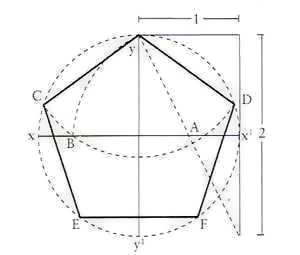
Actually it is possible that if those people who were trying to decipher the “Names Of God” would have turned to geometry, they would have uncovered the big cosmic secret. If the symbol of the foundation of creation is the Monad, the circle with the dot in the middle, what would happen if we would use the number 72? The circle is divided to 360 degrees since the days of the ancient Sumerians some 5000 years ago. Dividing the circle by 72 gives us five points from which we derive the Pentad. The Pentad was so secret and sacred in ancient times and the Pythagoreans used it as a secret mark to identify one another. They studied the geometric properties of the shape rigorously and since it was so secret to them the knowledge was passed on only orally.
Knowledge of the Pentad resurfaced only during the Renaissance in Luca Pacioli's book (illustrated by Leonardo de Vinci) “De Divina Proportione” (The Devine Proportion) meaning the Golden Ratio. From the Pentad we can produce the Golden Ratio, if we use a triangle at an angle of 72 degrees we reach the Golden Ratio again. Of the Pentad, one of the five Platonic solids can be derived, the Dodecahedron. The use of the Platonic Solids (5 polyhedron structures , each being constructed from identical polygons) by Greek philosophers was common and they saw them as the elements of the universe, the Dodecahedron being the most important.
The Renaissance
During the Renaissance some intensive research was done on the Golden Ratio, the 5 Platonic solids, and the Thirteen Archimedean Solids.
The search for the use of geometric structures lead me to the famous and laden with symbology creation of Albrecht Dürer from 1514: Melancholia I. The old engraving depicts a winged character which represents the artist himself searching for the truth. The character is holding a compass and looking at a geometric structure. In the engraving, an hourglass is seen which represents that time is running out, and also a magic square with the number 34 which probably represent Jupiter. There are also other symbols with esoteric meaning. An examination of the structure of the engraving raises the conclusion most researchers agree on, that the base of the diamond like structure is based on the angle 72.
Observation of Luca Pacioli's painting from 1495 reveals to us the tight link between geometry, the Golden Ratio, and art. In the picture we see Luca Pacioli drawing one of Euclid's theorem and looking at a glass structure of one of the Archimedean Solids (the Rhombicuboctahedron) filled half way with water. On the table next to him a Dodecahedron appears (and by the way the other figure is probably Albrecht Dürer).

So what is the hidden key which everyone has been searching for?
As I was looking at the Tetractys and seeing how the letters of the name of God in Hebrew create the number 72, I realized that there was probably a tight connection between the Pythagoreans and the kaballa.
Jewish Kaballa tried to tie between man and God and encrypted the idea that the human being can unite and become ONE with the CREATOR itself and become a creator by himself-this knowledge was hidden in esoteric symbolism. According to Jewish tradition, the secret formula to the universe is comprised of 216 letters and of 72 triple combinations. If we go back to the Bible and examine the numerical symbology that is found there, we will find (as I had already mentioned) that the proportions of Noah's ark are close to the Golden Ratio and the measurements of the ark circle around the number 3 and f which are a part of the Fibonacci sequence.
In the story of Elijah on Mt. Carmel there is the use of the number 12 and there is a symbolic duplication that Elijah performs of 12*12 which is 144, the 12th number in the Fibonacci sequence. If we add the use of the 72 names of God and the explicit name of 216 letters we find that we get only one thing – a Dodecahedron. The 72, 216, and 144 are all part of the five angles of the Pentad we create out of the circle. The 3 and the 5 being the geometric definition of the base of the Dodecahedron (3 Pentads around each vertex), the number 12 being the number of facets of the Dodecahedron.
The more you gaze at the same old symbology, you realize that the ancients tried to find the way to the secrets of creation itself. The perception of the link between MAN and CREATION and seeing them as a micro-universe is the big secret of the philosophers and the mystics.
In the books of Heinrich Cornelius Agrippa, the 16th century astrologist and alchemist, the human body is depicted in parallel to a Pentad and other geometric structures. The entire universe and the Creator itself are reflected in each of us and in the ability of each of us to reach the same divine abilities.
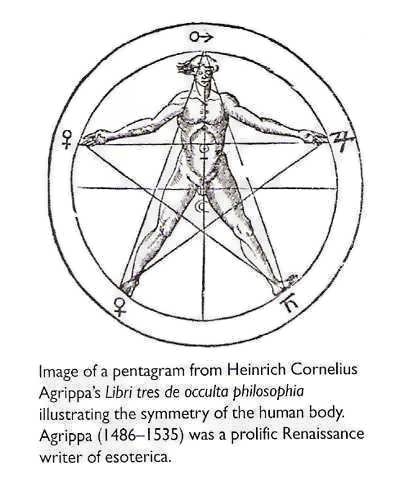 All of creation was formed in order for the Creator or this unity to learn and experience itself, because in a state of unity there is no relativity. The one can not experience itself.
When those ancient philosophers began studying the universe through those geometric mathematical rules they were the micro studying the macro, or in other words it is the universe studying itself. Each of us is a reflection of the universe and the Creator itself. When I searched for a symbol for this idea I came back to Leonardo de Vinci and Luca Pacioli. One of the structures that appears in the book De Divina Proportione and in Luca Pacioli's famous picture is the Rhombicuboctahedron – one of the 13 Archimedean solids. When the structure, as it appears in the painting, is examined closely, a reflection of the room can be seen and the view that is seen from beyond the window. The reason for this is that a spherical panoramic picture of 360 degrees can be projected on this shape in 180 degree precisely. As a symbol, it is a structure that to me represents how the universe experiences itself through our eyes.
Some years ago, scientists in the field of cosmology began measuring trace radiation from the big bang. Their calculations produced an interesting result. According to the latest calculations, our universe is finite and its structure is a Dodecahedron.
How did those ancient philosophers reach that same understanding thousands of years ago? The answer is that all those geometric rules show us that we are the pattern of the universe itself and the knowledge of the universe exists in us and is waiting to be discovered.
The Divine Reflection
The Christ Grid pendant
|
|
|
|
Reply |
Message 7 of 7 on the subject |
|
ALQUIMIA-DIMENCIONES DE LA GRAN PIRAMIDE-RELACION CON EL 911, CON LAS DIMENCIONES DE LA TIERRA Y LA LUNA Y CON EL CHIVO EXPIATORIO (DIA DE LA EXPIACION)-PATRON GIZE-MENSAJE ROSE LINE DECODIFICADO PARA GLORIA DE YHWH TODOPODEROSO-RELACION CON EL 911 O 711 (11 DE SEPTIEMBRE)
DIAMETRO TIERRA=7920 millas inglesas=720x11
RADIO TIERRA=3960 millas inglesas
RADIO LUNA=1080 millas inglesas
ALTURA PIRAMIDE=3960+1080 millas=5040 millas=720X7
EL 11 DE SEPTIEMBRE O 11/7 ESTA CODIFICADO EN LA GRAN PIRAMIDE DE GIZE EN FUNCION AL RADIO DE LA TIERRA Y DE LA LUNA.
NUMERO DE ORO PHI= (RAIZ CUADRADA DE 5040 ELEVADO AL CUADRADO MAS 3960 AL CUADRADO)/ 3960 = 1.618033
(3960 * 3960) + (5040 * 5040) = 41083200
SQRT 41083200= 6409.61
El radio de la tierra mas el radio de la luna equivalen al RADIO DEL CIRCULO, CUYA CIRCUNFERENCIA EQUIVALE AL PERIMETRO DEL CUBO QUE CONTIENE LA TIERRA. (ALQUIMIA)
LA GRAN PIRAMIDE, EN FUNCION AL NUMERO DE ORO, ESTA DISEÑADA EN EL CONTEXTO A LA DIVISION DEL APOTEMA SOBRE EL RADIO DE LA TIERRA QUE EQUIVALE A LA MITAD DEL LADO DEL CUADRADO DE SU SUPERFICIE.
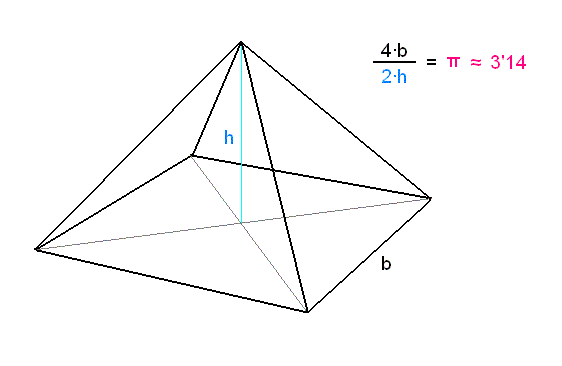

La base de la Gran Pirámide es un cuadrado de 230 metros de lado, caben 8 campos de fútbol. El suelo rocoso donde se asientan las pirámides está exactamente nivelado. El vértice superior de la pirámide a 147 metros de altura coincide con el centro de la base del cuadrado de 230m x 230m.
Medidas según Flanders Petrie
- Lado N: 230,364 m.
- Lado E: 230,319 m.
- Lado S: 230,365 m.
- Lado O: 230,342 m.

Fig 7 . Cuadratura del círculo
El perímetro de la base de la Gran Pirámide es el mismo que el de la circunferencia dada, tomando como radio la altura de ésta, o, lo que es lo mismo, dividiendo el perímetro de la base de la Gran Pirámide por el doble de la altura obtenemos el número Pi.
El perímetro total de la base de la Gran Pirámide p= 23o x 4= 920 metros
Perímetro de la circunferencia 2Пr= 2x(3,1416)x(146,347)= 919,20 metros
Considerando que la base de la GRAN PIRAMIDE TIENE 230 METROS (METRO ESTA DISEÑADO EN FUNCION A ROSE LINE), en el contexto a que EL RADIO ES LA MITAD DEL DIAMETRO, ES OBVIO QUE LA RELACION PROPORCIONAL ES LA MITAD DEL LADO DEL CUADRADO, OSEA 230/2=115 (NUMERO INTERRELACIONADO CON EL PERIODO SIDEREO DE MERCURIO QUE JUSTAMENTE TAMBIEN TIENE REFERENCIA AL NUMERO PI Y CON EL DIA DE SAN MARCOS, OSEA EL 25 DE ABRIL, DIA NUMERO 115 DEL AÑO GREGORIANO. AQUI SE CONFIRMA MATEMATICAMENTE QUE NUESTRO SEÑOR JUSTAMENTE EN MATEO 16:18 ESTABA HACIENDO REFERENCIA A LA GRAN PIRAMIDE Y AL VATICANO, QUE ESTAN DISEÑADOS EN FUNCION A LA CONSTELACION DE LAS PLEYADES Y ORION, EN EL CONTEXTO AL NUMERO DE ORO Y AL GRIAL=JUAN MARCOS.
SI SACAMOS EL APOTEMA tenemos que hacer la RAIZ CUADRADA DE 115 AL CUADRADO MAS 147 AL CUADRADO (TEOREMA DE PITAGORAS) , QUE ES LA ALTURA AL CUADRADO.
115*115+147*147=34834
RAIZ CUADRADA 34834=186.63868837944614 METROS
PHI=186.63868837944614/115=1.62294511634301 (APROXIMADAMENTE PORQUE TOMAMOS NUMEROS REDONDOS PERO ES UNA APROXIMACION DE PHI=1.618033)
INCREIBLE PORQUE EL APOTEMA EQUIVALE A LA CANTIDAD DE DIAS QUE HAY EN EL CALENDARIO LUNI-SOLAR HEBREO DESDE EL PRIMERO DEL PRIMER MES HASTA EL DIA DE LA EXPIACION 9 Y 10 DEL SEPTIMO MES HEBREO QUE FUE EL CORAZON DEL 911.
EL GRIAL, CODIFICADO EN LA BASE DE LA GRAN PIRAMIDE EN EL CONTEXTO AL 911
LEVITICO 23
f) El día de la expiación (YOM KIPUR)
23:26 Habló Yahveh a Moisés, diciendo:
23:27 Además el día décimo de este séptimo mes será el día de la Expiación,  en el cual tendréis reunión sagrada; ayunaréis y ofreceréis manjares abrasados a Yahveh. en el cual tendréis reunión sagrada; ayunaréis y ofreceréis manjares abrasados a Yahveh.
23:28 No haréis en ese mismo día ningún trabajo, pues es el día de Expiación, en el que se ha de hacer la expiación por vosotros   delante de Yahveh, vuestro Dios. delante de Yahveh, vuestro Dios.
23:29 El que no ayune ese día será exterminado de entre su pueblo.
23:30 Al que haga en tal día un trabajo cualquiera, yo lo haré perecer de en medio de su pueblo.
23:31 No haréis, pues, trabajo alguno. Es decreto perpetuo, de generación en generación, dondequiera que habitéis.
23:32 Será para vosotros día de descanso completo y ayunaréis; el día nueve del mes, por la tarde, de tarde a tarde, guardaréis descanso.
23:33 Habló Yahveh a Moisés, diciendo:
EL NUEVE DEL SEPTIMO MES ES EL DIA NUMERO 186 DEL CALENDARIO LUNI-SOLAR HEBREO, EL MISMO DIA DEL 911, EN EL CONTEXTO AL DISEÑO DE LA BASE EN METROS PATRON DE LA MISMA GRAN PIRAMIDE EN EL CONTEXTO A LA VELOCIDAD DE LA LUZ. ESE ES EL VERDADERO MENSAJE DE LA ESTATUA DE LA LIBERTAD
|
|
|
|
 First
First
 Previous
2 a 7 de 7
Next
Previous
2 a 7 de 7
Next
 Last
Last

|

