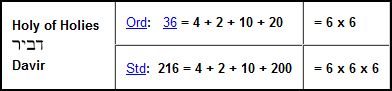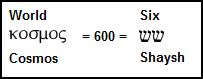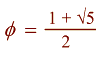|
|
http://www.youtube.com/watch?v=j9e0auhmxnc
Phi in the Bible
Although perhaps not immediately obvious, phi and the golden section also appear in the Bible. Also see the Theology page.
The Ark of the Covenant is a Golden Rectangle
|

|
In Exodus 25:10, God commands Moses to build the Ark of the Covenant, in which to hold His Covenant with the Israelites, the Ten Commandments, saying,
"Have them make a chest of acacia wood-
two and a half cubits long,
a cubit and a half wide,
and a cubit and a half high."
|
The ratio of 2.5 to 1.5 is 1.666..., which is as close to phi (1.618 ...) as you can come with such simple numbers and is certainly not visibly different to the eye. The Ark of the Covenant is thus constructed using the Golden Section, or Divine Proportion. This ratio is also the same as 5 to 3, numbers from the Fibonacci series.
In Exodus 27:1-2, we find that the altar God commands Moses to build is based on a variation of the same 5 by 3 theme:
"Build an altar of acacia wood, three cubits high; it is to be square, five cubits long and five cubits wide."
Note: A cubit is the measure of the forearm below the elbow.
|
 |
|
Noah's Ark uses a Golden Rectangle
|
In Genesis 6:15, God commands Noah to build an ark saying,
"And this is the fashion which thou shalt make it of: The length of the ark shall be three hundred cubits, the breadth of it fifty cubits, and the height of it thirty cubits."
Thus the end of the ark, at 50 by 30 cubits, is also in the ratio of 5 to 3, or 1.666..., again a close approximation of phi not visibly different to the naked eye. Noah's ark was built in the same proportion as ten arks of the covenant placed side by side.
|

|
The Number 666 is related to Phi
|

|
Revelation 13:18 says the following:
"This calls for wisdom. If anyone has insight, let him calculate the number of the beast, for it is a man's number. His number is 666."
|
| This beast, regarded by some as the Anti-Christ described by John, is thus related to the number 666, one of the greatest mysteries of the Bible.
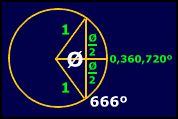
Curiously enough, if you take the sine of 666º, you get -0.80901699, which is one-half of negative phi, or perhaps what one might call the "anti-phi." You can also get -0.80901699 by taking the cosine of 216º, and 216 is 6 x 6 x 6.
The trigonometric relationship of sine 666º to phi is based on an isosceles triangle with a base of phi and sides of 1. When this triangle is enclosed in a circle with a radius of 1, we see that the lower line, which has an angle of 306º on the first rotation and 666º on the second rotation, has a sine equal to one-half negative phi.
In this we see the unity of phi divided into positive and negative, analogous perhaps to light and darkness or good and evil. Could this "sine" be a "sign" as well?
In addition, 666 degrees is 54 degrees short of the complete second circle and when dividing the 360 degrees of a circle by 54 degrees you get 6.66... The other side of a 54 degree angle in a right angle is 36 degrees and 36 divided by 54 is .666.
Phi appears throughout creation, and in every physical proportion of the human body. In that sense it is the number of mankind, as the mysterious passage of Revelation perhaps reveals.
Also see the Theology page.
The colors of the Tabernacle are based on a phi relationship
The PhiBar program produces the colors that the Bible says God gave to Moses for the construction of the Tabernacle.
As it says in Exodus 26:1, "Make the tabernacle with ten curtains of finely twisted linen and blue, purple and scarlet yarn, with cherubim worked into them by a skilled craftsman."
Set the primary color of the PhiBar program to blue, the secondary color of the PhiBar to purple and it reveals the Phi color to be scarlet.
This reference to the combination blue, purple and scarlet in the construction of the tabernacle appears 24 times in Exodus 25 through 39, describing the colors to be used in the curtains, waistbands, breastpieces, sashes and garments.
See the Color page for additional information.
|
Insights on the Ark of the Covenant and 666 contributed by Robert Bartlett.
Insights on the Altar in Exodus 27 contributed by Sir Hemlock.
Insights on the Tabernacle colors contributed by J.D. Ahmanson.
http://goldennumber.net/bible.htm
|
|
|
|
|
|
The Golden Mean can be construed as the basis of philosophy and Sacred Geometry, one of the Transcendental Numbers, [*] and is typically derived from Fibonacci Numbers. [* Technically, from a strictly mathematical standpoint -- as has been pointed out by several readers -- the Golden Mean, Phi, is the solution to a polynomial equation and thus not mathematically transcendental. However, if one looks at the other definitions of transcendental, most would agree that it qualifies.]
According to Robert Lawlor [1], “Ancient geometry rests on no a priori axioms or assumptions. Unlike Euclidian and the more recent geometries, the starting point of ancient geometric thought is not a network of intellectual definitions or abstractions, but instead a meditation upon a metaphysical Unity, followed by an attempt to symbolize visually and to contemplate the pure, formal order which springs forth from this incomprehensible Oneness. It is the approach to the starting point of the geometric activity which radically separates what we may call the sacred from the mundane or secular geometries. Ancient geometry begins with One, while modern mathematics and geometry being with Zero.”
Other authors have noted that “Both the ancient Greeks and the ancient Egyptians used the Golden Mean when designing their buildings and monuments.” “Artists as diverse as Leonardo da Vinci and George Seurat used the ratio when constructing their paintings. These artists and architects discovered that by utilizing the ratio 1 : 1.618..., they could create a feeling of order in their works. Even today, artists are still using this proportion in their works, and scientists, like Roger Penrose are discovering new things about the Golden Mean and its place in science, mathematics, and nature.”
<http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibInArt.html> is an excellent website on the subject, and notes among many other things, the connection with classical music and the Golden Mean. In a 1996 article in the American Scientist, for example, Mike Kay reported that Mozart’s sonatas were divided into two parts exactly at the Golden Mean point in almost all cases. Inasmuch as Mozart’s sister had said that Amadeus was always playing with numbers and fascinated by mathematics, it appears that this was either a conscious choice or an intuitive one. Meanwhile, Derek Haylock noted that in Beethoven’s Fifth Symphony (possibly his most famous one), the famous opening “motto” appears in the first and last bars, but also at the Golden Mean point (0.618) of the way through the symphony, as well as 0.382 of the way (i.e., the Golden Mean squared). Again, was it by design or accident? Keep in mind that Bartók, Debussy, Schubert, Bach and Satie may have also deliberately used the Golden Mean in their music.
(6/6/05) Another excellent website is http://goldennumber.net. This one even includes phi to 20,000 decimal places -- just in case you need this for your next term paper. In particular, one might also want to check out Pascal's Triangle. The latter is just too strange for words, incorporating as it does Fibonacci Numbers.
In a much more esoteric vein, Ronald Holt, Director, of the Flower of Life Research has included in <http://www.floweroflife.org/spiral01.htm>, “To The Golden Spiral In All of Us” (dated April 21, 1999), in which he notes, “Sacred geometry is the study of geometric forms and their metaphorical relationships to human evolution as well as a study in fluid evolutionary transitions of mind, emotions, spirit, and consciousness reflected in the succeeding transition from one sacred geometric form (consciousness state) into another.”
Furthermore, “True sacred geometric forms never fixate or stagnate on one single form. Instead they are actually in constant fluid transcendence and change (evolve or devolve) from one geometric form to another at their own speed or frequency."
(5/31/05) The Golden Spiral, in fact, has been found in Crop Circles -- sort of Mother Nature's "performance art" in wheat and other crop fields -- and thus do sort of grow on you. An excellent description of this design is given by ka-gold's golden spiral.
FfFfFfFfFfFfFfFfFfFfFfFfFfFfFfFfFfFfFfFfFfFfFfFfF
The Golden Mean can be determined via geometry by taking a square with all sides equal to 1, drawing an arc with the center of radius at the midpoint of one side and through the corner of an opposite side, and extending the original side to where it intersects the arc.
The length of the extension will then exactly equal f [and the base’s total length being F.] From this same geometry, we can calculate F by noting that the diagonal in the square from the midpoint of one side to an opposite corner is equal to the square root of the sum of the squares of the opposite sides (i.e. 1 and 1/2) as per the Pythagorean Theorem. From this, we calculate the square root of 5/4 (1.11803398875...), and then add 1/2 the side, to obtain 1.61803398875...
The ancient Greeks, who were really into aesthetic geometric appeal, established as one of their primary axioms concerning proportion, to always use the golden mean in dividing a line, i.e. dividing it at a point, C, on the line AB:
A________________C_________B
such that:
AB/AC = AC/BC = 1.6180339875...
For clarity, the Golden Mean can be assumed to be either one of two values, given by [2]:
F = 1.61803 39887 49894 84820 45868 34365 63811 77203 09180...
or
f = 0.61803 39887 49894 84820 45868 34365 63811 77203 09180...
The Golden Mean, the number, is the only number in which, among other things, satisfies the mathematical relationships:
F = 1/F + 1 ; f = 1/f - 1
For the esoteric crowd, f can also be represented by the very strange equation:
f = 1 + 1/{1 + 1/[1 + 1/(1 + 1/{1 + 1/[1 + 1/(1 + ...)]})]}
Another way to view the above equation is to think of it as representing rabbits attempting to draw their family tree in a furry, more prolific version of Roots. [This aside is reference to one original example of the usefulness of Fibonacci Numbers, which mathematically is the easiest manner to obtain the values of the Golden Mean (and to as many powers as one might like) by simply dividing one member of the Fibonacci Series with another.]
In fact, the Golden Mean Mathematics is a whirlwind of fascinating mathematical ideas and curiosities. Suffice it to say -- for the mathematically-less-inclined -- that the Golden Mean is: 1) intimately tied to the number 5 (and in particular to regular pentagons and five-pointed stars), 2) relates directly to the ideal human body (i.e. the Golden Mean raised to various powers are indicative of the body’s proportions), and 3) has been used extensively in ancient (and modern!) architecture -- among other things.
In the relationship between F, f, and 5 (they even sound alike!), we take a 5-pointed star -- the points of which form an inscribed five-sized, regular pentagon. By an arbitrary choice of measurement units, the length of a line drawn from one point of the star to an opposite point, can be set equal to f. This results in the line between two adjacent points (one side of the pentagon) automatically equaling f2. The line from a point to the interior pentagon is then f3, the side of the interior pentagon is f4, and so forth, ad infinitum. Then by connecting these points in sequence, we suddenly discover we’ve been thrown a curve: a new geometrical delight known as The Golden Spiral.
We might also mention in passing that the connection of the Golden Mean to the five-pointed star may be why the sacred practice of Wicca seems so preoccupied with this universal symbol -- regardless of whether or not their practitioners fully understand the significance. (Or why flags of many nations, states, or corporations -- the latter such as Texaco and others -- all enthusiastically use the five pointed star! Not that these nations, states, etceteras, are practicing Wicca, but... Well... You understand!)
With respect to the body proportions, this point can be demonstrated by taking the measurements of the average of many people -- with women’s measurements (for some inexplicable reason) approaching the ideal more closely than men -- whereupon we find that the position of the navel (a human’s first channel of nourishment and life) divides the body’s height at precisely the Golden Mean. Furthermore, if the distance from the brow (top of the eye) to the nose is 1, then the distance from the brow to the crown is F. Going in the opposite direction, the distance from the nose to the base of the neck is F, the neck to the armpit is F2, the armpit to the navel is F3, the navel to the reach of the fingers is F4, and the distance from the fingertips to the soles is F5. On a smaller scale, in measuring the length of the bones in the human hand, we find measurements of 1, F, F2, and F3 (the last bone being within the palm of the hand).
The below drawings, courtesy of Michael S. Schneider [3], emphasize these points.
Beginning to get a hand on this? Michael S. Schneider [3], for example, notes that: “The body’s structure is a mirror of our psyche, a denser expression of the energetic patterns of our soul. Body and soul somehow partake of the same design. But in what way can a mathematical ratio permeate our souls? Through beauty. A deep part of ourselves recognizes in flowers and dancers the beauty of the mathematical infinite and sees in it the endlessness of our own depths. Natural beauty resonates with the archetypal nature within us.”
On a decidedly more mundane application of such “natural beauty”, investors in the stock market have used the delights of the Golden Mean for the purpose of making money and, hopefully, large wheelbarrows of it! As it turns out, F and f are important in the stock market, where the index averages (such as the Dow Jones Industrial Average) typically rise a certain number of points (say a hundred), and then fall back a number of points equal to 0.618 x 100, before again rising to new heights. The amount of the initial leg of this cycle is not always clear, but the retreat path is much more clearly defined.
Obviously, this cyclical nature also works in the opposite direction as well (a fact which novice investors might want to keep in mind). It must be noted that there are any number of variations in the amount of the market’s rise and fall, as well as variations in the time periods from minutes to decades. In effect, there are numerous cycles within cycles within cycles. Nevertheless, this predictive technique (known as Elliott Wave Theory) has been practiced successfully by numerous stock market analysts, who seem to have an unusually deep appreciation for F Lo Sophia and the money it can effortlessly make them.
There now seems to be a justifiable reason for our ancient ancestors having such a reverence toward the Golden Mean. Besides The Great Pyramids, their architecture showed it through such examples as the west facade of the Greek Parthenon, which perfectly fits within a golden rectangle (whose dimensions are 1 and F). The west facade of the Notre Dame Cathedral in Paris is also loaded with Golden Mean ratios, and more recently, the United Nations Building in New York City is designed as three golden rectangles (equivalent to three Parthenons stacked upon one another). Perhaps we shouldn’t attribute all our knowledge of the Golden Mean to the ancients, as such examples of Sacred Geometry keep cropping up in more modern structures. At least those designed by more “enlightened” architects.
Why? Because even artists with absolutely no interest in math (or an aversion to the subject) will inevitably respond to the beauty in the architecture which arises from the mathematics! This is likely true of everything from “cubism” to Mozart. For it is the mathematical resonance within the sacred geometry symbolism which touches our soul.
The Golden Mean also touches such intriguing phenomena as The Fifth Element, the Harmony of the Spheres, Connective Physics, Philosophy and the Tree of Life.
|
|
|
|
|
Golden Ratio
The golden section is a line segment divided according to the golden ratio: The total length a + b is to the length of the longer segment a as the length of a is to the length of the shorter segment b
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal tothe ratio of the larger quantity to the smaller one. The golden ratio is an irrationalmathematical constant, approximately 1.6180339887.[1] Other names frequently used for the golden ratio are the golden section (Latin: sectio aurea) and golden mean.[2][3][4] Other terms encountered include extreme and mean ratio,[5] medial section,divine proportion, divine section (Latin:sectio divina), golden proportion, golden cut,[6] golden number, and mean of Phidias.[7][8][9] In this article the golden ratio is denoted by the Greek lowercase letter phi ( 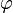 ) , while its reciprocal, ) , while its reciprocal,  or or  , is denoted by the uppercase variant Phi ( , is denoted by the uppercase variant Phi (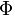 ). ).
Icosahedron Gold nanoparticle viewed in electron microscope.
Our Galena lead was polished following the Golden ratio and so converted into a Gold icosahedron
The ark of the Covenant
Detailed instructions[10] are given by God for the plan of the Ark: it is to be 2½ cubits in length, 1½ in breadth, and 1½ in height (as 21⁄2×11⁄2×11⁄2 royal cubits or 1.31×0.79×0.79 m). Then it is to be plated entirely with gold, and a crown or molding of gold is to be put around it. Four rings of gold are to be put into its four feet—two on each side—and through these rings staves of shittim-wood overlaid with gold for carrying the Ark are to be inserted; and these are not to be removed. A golden cover, adorned with golden cherubim, is to be placed above the Ark.
Although perhaps not immediately obvious, phi and the golden section also appear in the Bible.
|
|
In Exodus 25:10, God commands Moses to build the Ark of the Covenant, in which to hold His Covenant with the Israelites, the Ten Commandments, saying,
"Have them make a chest of acacia wood-
two and a half cubits long,
a cubit and a half wide,
and a cubit and a half high."
|
The ratio of 2.5 to 1.5 is 1.666..., which is as close to phi (1.618 ...) as you can come with such simple numbers and is certainly not visibly different to the eye. The Ark of the Covenant is thus constructed using the Golden Section, or Divine Proportion. This ratio is also the same as 5 to 3, numbers from the Fibonacci series.
In Exodus 27:1-2, we find that the altar God commands Moses to build is based on a variation of the same 5 by 3 theme:
"Build an altar of acacia wood, three cubits high; it is to be square, five cubits long and five cubits wide."
Note: A cubit is the measure of the forearm below the elbow. |
 |
|
Note : Acacia Wood synonym of Bitterness
Noah's Ark uses a Golden Rectangle
|
In Genesis 6:15, God commands Noah to build an ark saying,
"And this is the fashion which thou shalt make it of: The length of the ark shall be three hundred cubits, the breadth of it fifty cubits, and the height of it thirty cubits."
Thus the end of the ark, at 50 by 30 cubits, is also in the ratio of 5 to 3, or 1.666..., again a close approximation of phi not visibly different to the naked eye. Noah's ark was built in the same proportion as ten arks of the covenant placed side by side.
|
|
The Number 666 is related to Phi
|
|
Revelation 13:18 says the following:
"This calls for wisdom. If anyone has insight, let him calculate the number of the beast, for it is a man's number. His number is 666."
|
This beast, regarded by some as the Anti-Christ described by John, is thus related to the number 666, one of the greatest mysteries of the Bible.Curiously enough, if you take the sine of 666º, you get -0.80901699, which is one-half of negative phi, or perhaps what one might call the "anti-phi." You can also get -0.80901699 by taking the cosine of 216º, and 216 is 6 x 6 x 6.
The trigonometric relationship of sine 666º to phi is based on an isosceles triangle with a base of phi and sides of 1. When this triangle is enclosed in a circle with a radius of 1, we see that the lower line, which has an angle of 306º on the first rotation and 666º on the second rotation, has a sine equal to one-half negative phi.
In this we see the unity of phi divided into positive and negative, analogous perhaps to light and darkness or good and evil. Could this "sine" be a "sign" as well?
In addition, 666 degrees is 54 degrees short of the complete second circle and when dividing the 360 degrees of a circle by 54 degrees you get 6.66... The other side of a 54 degree angle in a right angle is 36 degrees and 36 divided by 54 is .666.
Phi appears throughout creation, and in every physical proportion of the human body. In that sense it is the number of mankind, as the mysterious passage ofRevelation perhaps reveals.
|

The Illuminati (plural of Latin illuminatus, "enlightened") is a name given to several groups, both historical and modern, and both real and fictitious. Historically, the name refers specifically to the Bavarian Illuminati, an Enlightenment-era secret society founded on May 1, 1776.
In modern times it is also used to refer to a purported conspiratorial organization which acts as a shadowy "power behind the throne", allegedly controlling world affairs through present day governments and corporations, usually as a modern incarnation or continuation of the Bavarian Illuminati. In this context, the Illuminati are believed to be the masterminds behind events that will lead to the establishment of a New World Order.
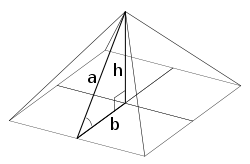 |
A regular square pyramid is determined by its medial right triangle, whose edges are the pyramid's apothem (a), semi-base (b), and height (h); the face inclination angle is also marked. Mathematical proportions b:h:a of  and and 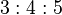 and and  are of particular interest in relation to Egyptian pyramids. are of particular interest in relation to Egyptian pyramids. |
|
|
|
|
|
Octahedron or bipyramid
The vertices of the octahedron lie at the midpoints of the edges of the tetrahedron, and in this sense it relates to the tetrahedron in the same way that the cuboctahedron and icosidodecahedron relate to the other Platonic solids. One can also divide the edges of an octahedron in the ratio of the golden mean to define the vertices of an icosahedron. This is done by first placing vectors along the octahedron's edges such that each face is bounded by a cycle, then similarly partitioning each edge into the golden mean along the direction of its vector. There are five octahedra that define any given icosahedron in this fashion, and together they define a regular compound.
Note {3,3} is the tetrahedron, {3,4} the octahedron followed by the icosahedron {3,5}
Icosahedron
It has five triangular faces meeting at each vertex. It can be represented by itsvertex figure as 3.3.3.3.3 or 35, and also by Schläfli symbol {3,5}. It is the dual of the dodecahedron, which is represented by {5,3}, having three pentagonal faces around each vertex.
Vertex figure of the Icosahedron
3.3.3.3.3
Vertex figure of the octahedron or bipyramid
3.3.3.3
 |
The owl ( Moloch ) Symbol of wisdom
Present in the dollar bill and the Bohemian Groove
|
 |
| The pact with Satan ( Golden fleece ) and the owl symbolizing wisdom |
Dimensions of the icosahedron
If the edge length of a regular icosahedron is a, the radius of a circumscribed sphere (one that touches the icosahedron at all vertices) is

and the radius of an inscribed sphere (tangent to each of the icosahedron's faces) is
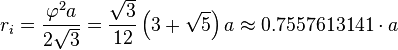
while the midradius, which touches the middle of each edge, is

Remember
Curiously enough, if you take the sine of 666º, you get -0.80901699, which is one-half of negative phi, or perhaps what one might call the "anti-phi." You can also get -0.80901699 by taking the cosine of 216º, and 216 is 6 x 6 x 6.
Electron microscopy suggests that many viruses are roughly spherical. A detailed examination shows that they are actually icosahedral. Icosahedral viruses are very common plant and animal viruses. The HIV capsid layer is thought to have an icosahedral structure. At the moment precise details of the HIV capsid structure are not known but some general considerations are described below:
The subunits of the capsid are located around the vertices or face of an icosahedron. An icosahedron has 20 equilateral triangles arranged around the face of a sphere. It is defined by having 2, 3 and 5 fold axis of symmetry.
Cartesian coordinates of the Icosahedron ( 3 Golden rectangles )
  If we join mid-points of the dodecahedron's faces, we can get three rectangles all at right angles to each other. What's more, they are Golden Rectangles since their edges are in the ratio 1 to Phi. The same happens if we join the vertices of the icosahedron since it is the dual of the dodecahedron. |
|
|
|
|
Using these golden rectangles it is easy to see that the coordinates of the icosahedron are as given above since they are:
(0,± 1, ± Phi), (± Phi, 0, ± 1), (± 1, ± Phi, 0) .
Icosahedron net
A geodesic gridis a technique used to model the surface of a sphere (such as the Earth) with a subdividedpolyhedron, usually an icosahedron.
Geodesic Dome
  A geodesic sphere and its dual.Stellation of the Icosahedron According to specific rules defined in the book The fifty nine icosahedra, 59 stellations were identified for the regular icosahedron. The first form is the icosahedron itself. One is a regular Kepler-Poinsot polyhedron. Three are regular compound polyhedra
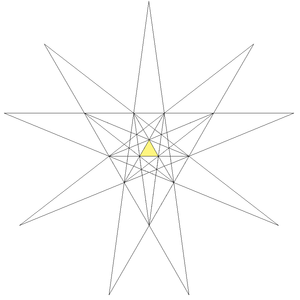
The stellation diagram for the icosahedron with the central triangle marked for the original icosahedronNote 9 pointed star
Official 911 emergency logo
Another version
Stellation diagram with numbered cellsNote 6 elevens, 6 nines and 6 six surrounding the inverted triangle A geodesic sphere and its dual.Stellation of the Icosahedron According to specific rules defined in the book The fifty nine icosahedra, 59 stellations were identified for the regular icosahedron. The first form is the icosahedron itself. One is a regular Kepler-Poinsot polyhedron. Three are regular compound polyhedra
The stellation diagram for the icosahedron with the central triangle marked for the original icosahedronNote 9 pointed star
Official 911 emergency logo
Another version
Stellation diagram with numbered cellsNote 6 elevens, 6 nines and 6 six surrounding the inverted triangle
Note: nine 13 pointed stars
Because of this annual exorcism of the noxious spirits of the dead, the whole month of May was rendered unlucky for marriages, whence the proverb Mense Maio malae nubent ("They wed ill who wed in May").
In the Julian calendar the three days of the feast were 9, 11, and 13 May. The myth of origin of this ancient festival, according to Ovid, who derives Lemuria from a supposed Remuria[2] was that it had been instituted byRomulus to appease the spirit of Remus (Ovid, Fasti, V.421ff; Porphyrius ). Ovid notes that at this festival it was the custom to appease or expel the evil spirits by walking barefoot and throwing black beans over the shoulder at night. It was the head of the household who was responsible for getting up at midnight and walking around the house with bare feet throwing out black beans and repeating the incantation, "I send these; with these beans I redeem me and mine (haec ego mitto; his redimo meque meosque fabis.)." nine times. The household would then clash bronze pots while repeating, "Ghosts of my fathers and ancestors, be gone!"[3] nine times.
On what had been the culminating day of the Lemuralia, May 13 in 609 or 610— the day being recorded as more significant than the year—, Pope Boniface IV consecrated the Pantheon at Rome to the Blessed Virgin and all the martyrs, and the feast of that dedicatio Sanctae Mariae ad Martyres has been celebrated at Rome ever since. According to cultural historians,[4] this ancient custom was Christianized in the feast of All Saints' Day, established in Rome first on May 13, in order to de-paganize the Roman Lemuria,[5] while others see a link to the May 13 date in Saint Ephrem's celebration of All Saints on that day in the 4th century.[6]
The number, "13" is considered divine by the occultist for a couple of reasons:
1. The Bible assigns '13' the meaning of "rebellion against constituted authority", plus the depravity that caused Satan to rebel against God.
2. The occultist assigns '6' to represent the number of man, and the number '7' to represent the number of divine perfection. Thus, as a person climbs that "Jacob's Ladder" toward self-perfection in the realm of the occult, the number '13' represents the state of divine perfection, self-achieved perfection, and Illumination (6+7 = 13).
Thus, the occult calendar is comprised of four periods of 13 weeks each. We list these periods for you, below.
Then, after listing them, we shall come back to talk about each of them in detail.
1. Winter Solstice - 13 weeks - Minor sabbath
a. December 21 - Yule
b. December 21-22 - Winter Solstice/Yule. One of the Illuminati's Human Sacrifice Nights
c. February 1 and 2 - Candlemas and Imbolg, a.k.a. Groundhog's Day. One of the Illuminati's Human Sacrifice Nights
d. February 14 - Valentine's Day
2. Spring Equinox - 13 weeks - Minor sabbath but does require human sacrifice
a. March 21-22 - Goddess Ostara - Note: Easter is the first Sunday after the first new moon after Ostara. March 21 is one of the Illuminati's Human Sacrifice Nights
b. April 1 - All Fool's Day, precisely 13 weeks since New Year's Day!
c. April 19 - May 1 - Blood Sacrifice To The Beast. Fire sacrifice is required on April 19.
d. April 30 - May 1 - Beltaine Festival, also called Walpurgis Night. This is the highest day on the Druidic Witch's Calendar. May 1 is the Illuminati's second most sacred holiday. Human sacrifice is required
|
|
|
|
|
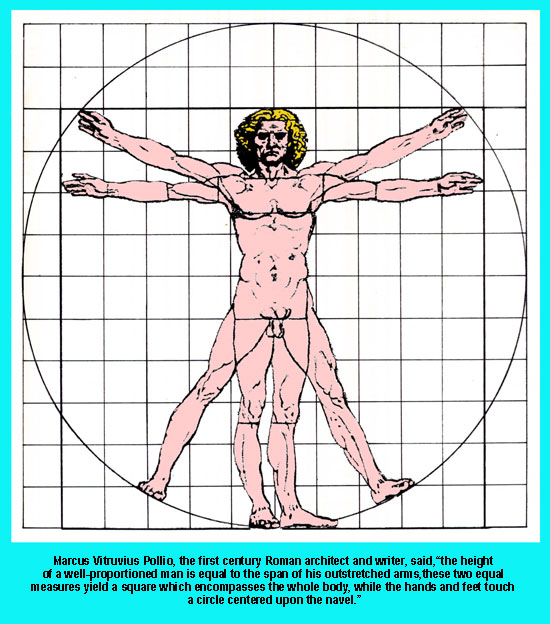
DaVinci’s Vitruvian Man
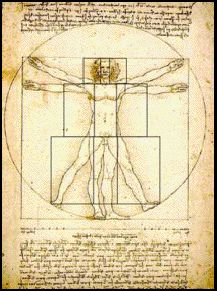
The Vetruvian Man"(The Man in Action)" by Leonardo Da Vinci
We can draw many lines of the rectangles into this figure. Then, there are three distinct sets of Golden Rectangles: Each one set for the head area, the torso, and the legs.
DaVinci named his drawing after Marcus Vitruvius Pollo, who as a 1st century Roman architect that stated ‘the height of a well-proportioned man is equal to the span of his outstretched arms, these two equal measured yield a square which encompasses the whole body, while the hands and feet touch a circle centered upon the navel.”
Vitruvius was a proponent of the ‘Sacred Geometry of Pythagoras’ and designed temples based upon the proportions of the human body.
Symboldictionary.net
According to Pythagorian tradition, the circle represents the spiritual realm; the square, material existence, so the human body represented the perfect marriage of matter and spirit, which was is reflected in its proportions. This perfection, wrote Vitruvius, was evidenced by the fact that the extended limbs of a perfectly proportioned human fit into both the circle and the square.
Kenneth Clark in his biography of DaVinci on pg 76 wrote:
“…for if man was the measure of all things, physically perfect man was surely the measure of all beauty, and his proportions must in some way be reducible to mathematical terms and correspond with those abstract perfections, the square, the circle, and the golden section.”
In short, Vitruvian man represents the ‘perfect man.’ The Beast.
Rev 13:18 Here is wisdom: Let the one having reason count the number of the beast, for it is the number of a man and its number is six hundred and sixty six.
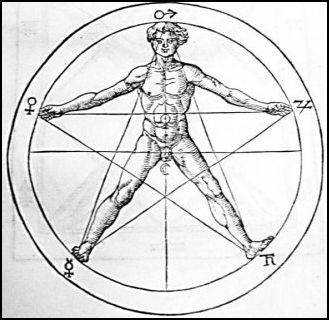
The Fibonacci pattern/Phi points to the mark
http://goldennumber.net/bible.htm
“This beast, regarded by some as the Anti-Christ described by John, is thus related to the number 666, one of the greatest mysteries of the Bible.
Curiously enough, if you take the sine of 666º, you get -0.80901699, which is one-half of negative phi, or perhaps what one might call the “anti-phi.” You can also get -0.80901699 by taking the cosine of 216º, and 216 is 6 x 6 x 6.
The trigonometric relationship of sine 666º to phi is based on an isosceles triangle with a base of phi and sides of 1. When this triangle is enclosed in a circle with a radius of 1, we see that the lower line, which has an angle of 306º on the first rotation and 666º on the second rotation, has a sine equal to one-half negative phi.
In this we see the unity of phi divided into positive and negative, analogous perhaps to light and darkness or good and evil. Could this “sine” be a “sign” as well?
In addition, 666 degrees is 54 degrees short of the complete second circle and when dividing the 360 degrees of a circle by 54 degrees you get 6.66… The other side of a 54 degree angle in a right angle is 36 degrees and 36 divided by 54 is .666.
Phi appears throughout creation, and in every physical proportion of the human body. In that sense it is the number of mankind, as the mysterious passage of Revelation perhaps reveals.”
http://www.biblewheel.com/gr/gr_216.asp
The Number 216 is the cube of 6 – the Number God used in the foundation of the Creation Holograph. It is the value of the Davir (Holie of Holies, called the Oracle in the verse above) which God designed as a physical cube of 20 x 20 x 20 cubits:
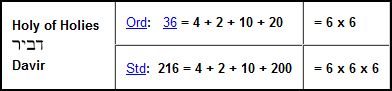
These identities integrate with the Holiness of the Number 6, which is the Number the Lord God Almighty used to construct the Cosmos (= 600). This is why the “Man of Sin” who sits in the Holy of Holies shewing himself to be God, is marked by the Number 666. It is his attempt to sit in God’s Holy Place.
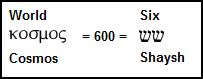
Further linking this concept together is the fact that the Ark of the Covenant was designed according to the Fibonacci pattern.
http://goldennumber.net/bible.htm
The Ark of the Covenant is a Golden Rectangle
In Exodus 25:10, God commands Moses to build the Ark of the Covenant, in which to hold His Covenant with the Israelites, the Ten Commandments, saying,
“Have them make a chest of acacia wood- two and a half cubits long, a cubit and a half wide, and a cubit and a half high.”
The ratio of 2.5 to 1.5 is 1.666…, which is as close to phi (1.618 …) as you can come with such simple numbers and is certainly not visibly different to the eye. The Ark of the Covenant is thus constructed using the Golden Section, or Divine Proportion. This ratio is also the same as 5 to 3, numbers from the Fibonacci series.
In Exodus 27:1-2, we find that the altar God commands Moses to build is based on a variation of the same 5 by 3 theme:
“Build an altar of acacia wood, three cubits high; it is to be square, five cubits long and five cubits wide.”
Note: A cubit is the measure of the forearm below the elbow.
The cubit is based on the Fibonacci pattern/Phi as well.

To further connect these ideas, the following is a study done from the author of the BibleWheel, Richard McGough.
http://www.biblewheel.com/GR/GR_666.asp

 The essential holiness of the Number 666 can not be denied. It is designed by God. It marks the Beast because the Beast seeks to blaspheme God and sit in the Holy Place, exactly where the Holy Ark = 666 sat! The essential holiness of the Number 666 can not be denied. It is designed by God. It marks the Beast because the Beast seeks to blaspheme God and sit in the Holy Place, exactly where the Holy Ark = 666 sat!
As a finally example, we have these multiple occurrences of the phrase “of/from God”:
In each case, the highlighted words are translated from the Greek phrase “para Theou.” We have the identity:

Yahshua came ‘Para Theou’
John 1.6: There was a man sent from God, whose name was John.
John 9.16: Therefore said some of the Pharisees, This man is not of God, because he keepeth not the sabbath day. Others said, How can a man that is a sinner do such miracles? And there was a division among them.
John 9.33: If this man were not of God, he could do nothing.
2 Peter 1.17: For he received from God the Father honour and glory, when there came such a voice to him from the excellent glory, This is my beloved Son, in whom I am well pleased.
2 John 3: Grace be with you, mercy, and peace, from God the Father, and from the Lord Jesus Christ, the Son of the Father, in truth and love.
In light of these identities, we must understand that God Himself is revealing the Number 666 as His own Number which marks the true intent of the the Devil, the Pseudochrist – i.e. False Christ, the true meaning of Antichrist – who would if he could, sit upon God’s Throne in the Holy of Holies, “shewing himself that he is God.”
The Holy of Holies had no light in it at all. The Holy Ark (= 666) – where God said He would meet with Moses – sat in complete darkness. This corresponds exactly with what the Lord said of Himself through the Prophet David in Psalm 18.11:
He made darkness his secret place; his pavilion round about him were dark waters and thick clouds of the skies.

His Secret Place is related to the Temple, in specific the Holy of Holies
Eze 7:22 I also will turn My face from them, and they shall defile My hidden place. And violent ones shall enter into it and defile it.
Psa 91:1 He who dwells in the secret place of the Most High shall abide in the shade of the Almighty.
Deu 27:15 Cursed is the man who makes a carved and molten image, an abomination to YHWH, the work of a craftsman’s hands, and who sets it up in a secret place! And all the people shall answer and say, Amen!
In the ark was placed the Word, which also linked to the Fibonacci Spiral. The Scriptures are divided into 66 books, further showing that the number 666 is a counterfeit ‘word.’
|
|
|
|
|
1.618 Phi, The Golden Ratio, God Creator of Heaven and Earth
|
|
|
|
|
THE MATH OF GOD – phi
 I have long been fascinated by the phenomena of phi (Greek letter), the Fibonacci number series, and the Divine proportion, Golden Proportion, Golden mean, Golden ratio, Golden spiral, Golden rectangle. To me this is such a clear evidence of God’s existence and His mighty genius in the creation of all things in nature. If you’ve never heard of this, look into it – you will be amazed! But here are some facts and examples to get you started. I have long been fascinated by the phenomena of phi (Greek letter), the Fibonacci number series, and the Divine proportion, Golden Proportion, Golden mean, Golden ratio, Golden spiral, Golden rectangle. To me this is such a clear evidence of God’s existence and His mighty genius in the creation of all things in nature. If you’ve never heard of this, look into it – you will be amazed! But here are some facts and examples to get you started.
 In mathematics, the Fibonacci series are the numbers in the following sequence of integers: In mathematics, the Fibonacci series are the numbers in the following sequence of integers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc. where the first two numbers are 0 and 1, and each subsequent number = the sum of the previous 2 numbers.
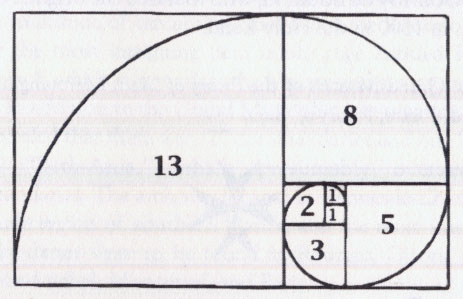
And Phi = 1.6180339887… or the ratio of any Fibonacci number to the previous number in the sequence, e.g. 8/5, 13/8, etc.

Golden Spiral
The Fibonacci series is named after Leonardo of Pisa, who introduced the sequence to Western European mathematics, although the sequence had been described earlier in Indian mathematics. Fibonacci numbers are used in the analysis of financial markets. They also appear in biological settings, such as branching in trees, arrangement of leaves on a stem , the fruit spouts of a pineapple , the flowering of an artichoke, an uncurling fern and the arrangement of a pine cone.
You can see this divine proportion of beauty in every aspect of creation, from botany to zoology, to the human body, the human face in particular, in the color spectrum, in musical scales and chords, in astronomy, in architecture, even in the patterns of our DNA! and especially for this post, in God’s instructions to the Jews in building such articles as the holy Ark of the Covenant, Noah’s Ark, the color arrangements in the Jewish Tabernacle in Exodus. God evidently designed the universe with this ratio as the basis of its appearance, from the microcosm to the macrocosm. Here are just a few examples of this phenomenon.
 A Nautilis seashell is one of the most exquisite examples of the divine proportion. A Nautilis seashell is one of the most exquisite examples of the divine proportion.
Some plants have beautiful repeating spiral patterns to their structures that incorporate the so-called golden angle (approx 137.5 degrees). Math buffs, artists, and mystics will appreciate that the golden angle is related to the “divine proportion” that frequently appears in aesthetically-pleasing forms.
 Plants with spiral patterns related to the golden angle also display another curious mathematical property. The seeds of a flower head form interlocking spirals in both clockwise and counterclockwise directions. The number of clockwise spirals differs from the number of counterclockwise spirals, and these two numbers are called the plant’s parastichy numbers (pronounced pi-RAS-tik-ee or PEHR-us-tik-ee). These numbers have a remarkable consistency. They are almost always two consecutive Fibonacci numbers. Plants with spiral patterns related to the golden angle also display another curious mathematical property. The seeds of a flower head form interlocking spirals in both clockwise and counterclockwise directions. The number of clockwise spirals differs from the number of counterclockwise spirals, and these two numbers are called the plant’s parastichy numbers (pronounced pi-RAS-tik-ee or PEHR-us-tik-ee). These numbers have a remarkable consistency. They are almost always two consecutive Fibonacci numbers.
Phi in the Bible and Creation
Although perhaps not immediately obvious, phi and the golden ratio appear in the Bible.
The Ark of the Covenant is a Golden Rectangle 
In Exodus 25:10, God commands Moses to build the Ark of the Covenant, in which to hold His Covenant with the Israelites, the Ten Commandments, saying, “Have them make a chest of acacia wood- two and a half cubits long, a cubit and a half wide, and a cubit and a half high.” The ratio of 2.5 to 1.5 is 1.666…, which is as close to phi (1.618 …) as you can come with such simple numbers and is certainly not visibly different to the eye. The Ark of the Covenant is thus constructed using the Golden Section, or Divine Proportion. This ratio is also the same as 5 to 3, numbers from the Fibonacci series.
In Exodus 27:1-2, we find that the altar God commands Moses to build is based on a variation of the same 5 by 3 theme: “Build an altar of acacia wood, three cubits high; it is to be square, five cubits long and five cubits wide.”
Note: A cubit is the measure of the forearm below the elbow.
Noah’s Ark uses a Golden Rectangle
In Genesis 6:15, God commands Noah to build an ark saying, “And this is the fashion which thou shalt make it of: The length of the ark shall be three hundred cubits, the breadth of it fifty cubits, and the height of it thirty cubits.” Thus the end of the ark, at 50 by 30 cubits, is also in the ratio of 5 to 3, or 1.666…, again a close approximation of phi not visibly different to the naked eye. Noah’s ark was built in the same proportion as ten arks of the covenant placed side by side.
The colors of the Tabernacle are based on a phi relationship
As it says in Exodus 26:1, “Make the tabernacle with ten curtains of finely twisted linen and blue, purple and scarlet yarn, with cherubim worked into them by a skilled craftsman.” This reference to the combination blue, purple and scarlet in the construction of the tabernacle appears 24 times in Exodus 25 through 39, describing the colors to be used in the curtains, waistbands, breastpieces, sashes and garments.
Phi relationships in a color spectrum produce rich, appealing color combinations
Michael Semprevivo has introduced a concept called the PhiBar, which applies phi relationships to frequencies, or wavelengths, in the spectrum of visible colors in light. Colors in the spectrum that are related by distances based on phi or the golden section produce very rich and visually appealing combinations. This is illustrated below on the screen shot of his PhiBar program. You can experiment with the PhiBar program, written in Visual Basic, by clicking HERE to download it and then running the .exe file.
 Note: This program is made available by Michael Semprevivo for free for non-commercial use only. The PhiBar.exe program was scanned with Norton’s Antivirus program on 03/01/2003 using current virus definitions and found to be virus free but no express or implied warranties are given with respect to its use. Note: This program is made available by Michael Semprevivo for free for non-commercial use only. The PhiBar.exe program was scanned with Norton’s Antivirus program on 03/01/2003 using current virus definitions and found to be virus free but no express or implied warranties are given with respect to its use.
The PhiBar produces the color combinations of the Tabernacle as described in the Bible
Using the PhiBar program above, J.D. Ahmanson discovered that it produces the colors that the Bible says God gave to Moses for the construction of the Tabernacle.
The DNA spiral is a Golden Section
The DNA molecule, the program for all life, is based on the golden section. It measures 34 angstroms long by 21 angstroms wide for each full cycle of its double helix spiral. 34 and 21, of course, are numbers in the Fibonacci series and their ratio, 1.6190476 closely approximates phi, 1.6180339.
Musical scales are based on Fibonacci numbers
 The Fibonacci series appears in the foundation of aspects of art, beauty and life. Even music has a foundation in the series, as: The Fibonacci series appears in the foundation of aspects of art, beauty and life. Even music has a foundation in the series, as:
There are 13 notes in the span of any note through its octave. A scale is composed of 8 notes, of which the 5th and 3rd notes create the basic foundation of all chords, and are based on whole tone which is 2 steps from the root tone, that is the 1st note of the scale.
Note too how the piano keyboard scale of C to C above of 13 keys has 8 white keys and 5 black keys, split into groups of 3 and 2. While some might “note” that there are only 12 “notes” in the scale, if you don’t have a root and octave, a start and an end, you have no means of calculating the gradations in between, so this 13th note as the octave is essential to computing the frequencies of the other notes. The word “octave” comes from the Latin word for 8, referring to the eight whole tones of the complete musical scale, which in the key of C are C-D-E-F-G-A-B-C.
In a scale, the dominant note is the 5th note of the major scale, which is also the 8th note of all 13 notes that comprise the octave. This provides an added instance of Fibonacci numbers in key musical relationships. What’s more, the typical three chord song in the key of A is made up of A, its Fibonacci & phi partner E, and D, to which A bears the same relationship as E does to A. This is analogous to the “A is to B as B is to C” basis for the golden section, or in this case “D is to A as A is to E.”
Musical instruments are often based on phi.
Fibonacci numbers and phi are used in the design of violins and even in the design of high quality speaker wire.

Have you seen enough? Isn’t God awesome in his precise and beautiful engineering? And to think that some still believe it all happened by chance! I could go on but this post is getting long! Do look into it yourself and be more amazed! Much of this information is taken from this website: http://goldennumber.net/index.htm .
http://graftedinelena.wordpress.com/2011/04/01/the-math-of-god-phi/
|
|
|
|
|
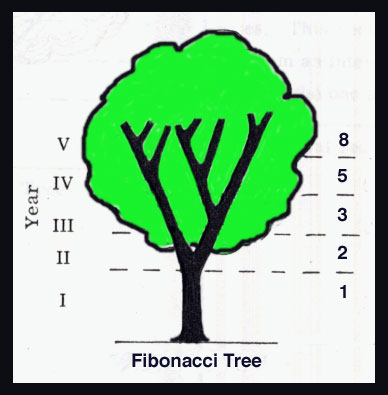
God's Handiwork -- Fibonacci Numbers
 hat are Fibonacci numbers? Discovered by Leonardo Fibonacci (1170-1250 A.D.) who was born in Pisa, Italy, the Fibonacci sequence is an infinite sequence of numbers, beginning: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... where each number is the sum of the two preceding it. Thus: 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 and so on. For any value larger than 3 in the sequence, the ratio between any two consecutive numbers is 1:1.618, or the Golden Ratio. hat are Fibonacci numbers? Discovered by Leonardo Fibonacci (1170-1250 A.D.) who was born in Pisa, Italy, the Fibonacci sequence is an infinite sequence of numbers, beginning: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... where each number is the sum of the two preceding it. Thus: 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 and so on. For any value larger than 3 in the sequence, the ratio between any two consecutive numbers is 1:1.618, or the Golden Ratio.
Known by the Greek letter phi, the Golden Ratio is an irrational number (i.e. one that cannot be expressed as the ratio or fraction of two whole numbers) with several curious properties. We can define it as the number that is equal to its own reciprocal plus one: phi = 1/phi + 1, with its value commonly expressed as 1.618,033,989. It's digits were calculated to ten million places in 1996, and they never repeat. It is related to Fibonacci numbers in that if you divide two consecutive numbers in the Fibonacci sequence, the answer is always an approximation of phi.
Also known as the Divine Proportion, the Golden Mean, or the Golden Section, this ratio is found with surprising frequency in natural structures as well as man-made art and architecture. where the ratio of length to width of approximately 1:1.618 is seen as visually pleasing. It is the point dividing a distance into two segments where the proportion of the smaller segment to the larger segment is the same as the larger to the whole.
Leaves On A Stem
If we look down on a plant, the leaves are often arranged so that leaves above do not hide leaves below. This means that each gets a good share of the sunlight and catches the most rain to channel down to the roots as it runs down the leaf to the stem.
The Fibonacci numbers occur when counting both the number of times we go around the stem, going from leaf to leaf, as well as counting the leaves we meet until we encounter a leaf directly above the starting one. If we count in the other direction, we get a different number of turns for the same number of leaves. One estimate is that 90 percent of all plants exhibit Fibonacci numbers in their leaf patterns.
Some common trees with their Fibonacci leaf arrangement numbers are:
1/2 elm, linden, lime, grasses
1/3 beech, hazel, grasses, blackberry
2/5 oak, cherry, apple, holly, plum, common groundsel
3/8 poplar, rose, pear, willow
5/13 pussy willow, almond
The numerator is # of turns and denominator is # of leaves til we arrive a a leaf directly under the starting leaf. Each leaf is this fraction of a turn after the last leaf. Or, there are so many turns (numerator) for every so many leaves (denominator).
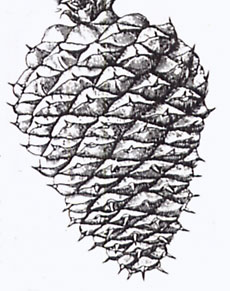
Cactus's spines often show the same spirals as we see on pine cones, petals and leaf arrangements, but they are much more clearly visible.
Plants illustrate the Fibonacci series in the numbers and arrangements of petals, leaves, sections and seeds. Plants that are formed in spirals, such as artichokes, pinecones, pineapples, daisies and sunflowers, illustrate Fibonacci numbers. Many plants produce new branches in quantities that are based on Fibonacci numbers.
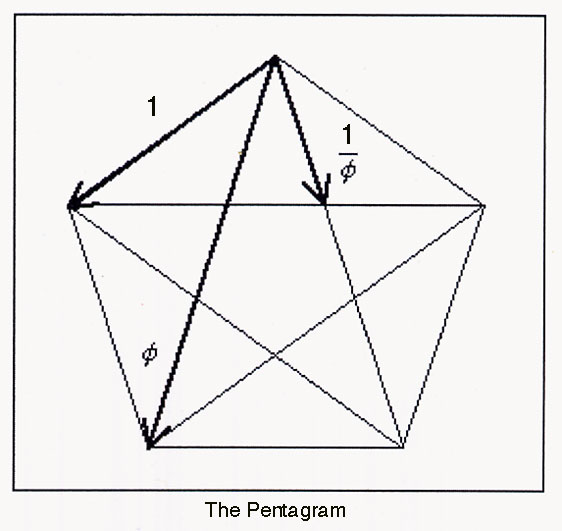
Calla Lilies have one petal. Euphorbia have two petals. Lilies have three. Buttercups, Roses, Pinks and Geraniums have five, Delphiniums and Bloodroot have 8 petals, Marigolds and Ragworts have 13, Asters and Black-eyed Susans 21, Pyrethrum have 34, and most Daisies have 34, 55, or 89. You don't find any other numbers very often. (The main exceptions are when those same numbers appear doubled, or when the so-called anomalous series appears: 3, 4, 7, 11, 18 and so on.). The five-pointed star is unusually common in nature. Not only in flowers, but also in the starfish, sand dollar, apple, etcetera. Why? Because Phi is the ratio of the side of a pentagon to its diagonal (see picture).
The Sunflower, Pinecone, Daisy and Nautilus Shell
Furthermore, the SUNFLOWER has 21 spirals on its head in one direction and 34 going in the other -- consecutive Fibonacci numbers. Or 34 and 55, or 55 and 89, or 89 and 144. The precise numbers depend on the species of SUNFLOWER.The same is true with DAISIES. The outside of a PINECONE has spirals that run clockwise and counterclockwise, and the ratio of the number of spirals is sequential Fibonacci values. In the elegant curves of a NAUTILUS shell, each complete new revolution will be a ratio of 1:1.618, when compared to the distance from the center of the previous spiral. If the divergence angle of a SUNFLOWER varies from 137.5 degrees (seen in the pattern below) to either 137.4 or 137.6 degrees, much of the beauty of the spiral is lost as well as its most compact arrangement. The SUNFLOWER therefore is in a precise state of perfection. ROMANESQUE BROCCOLI/CAULIFLOWER is Fibonacci spiral upon spiral. The same can be said of any other plant or animal containing this Fibonacci sequence. Everything in nature is already in a state of perfection -- contrary to the theory of Evolution..Where are the transitional stages? Where are the vestigial organs? Where are the imperfect spirals? Who told a DAISY to have the same Fibonacci sequence as a NAUTILUS, or a PINECONE, or a SUNFLOWER, or a RAM'S HORN or even the appearance of a BREAKING WAVE? None of them have a brain. None of them are in any way related to the other. Design demands a Designer. Beauty demands a Master Artist.
The Human Head
Human beauty is based on the Divine Proportion. Many experiments have been carried out to prove that the proportions of the top models' faces conform more closely to the Golden Ratio than the rest of the population. The human face is based entirely on Phi .The head forms a golden rectangle with the eyes at its midpoint. The mouth and nose are each placed at golden sections of the distance between the eyes and the bottom of the chin. The ear reflects the shape of a Fibonacci spiral. Even the dimensions of our teeth are based on phi. The front two incisor teeth form a golden rectangle, with a phi ratio in the heighth to the width. The ratio of the width of the first tooth to the second tooth from the center is also phi. The ratio of the width of the smile to the third tooth from the center is phi as well.
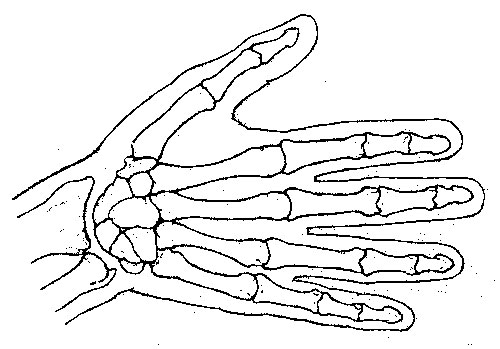
The Human Finger Joints and Hand
Each segment of each finger, from the tip to the base of the wrist, is larger than the preceding one by about the Fibonacci ratio of 1.618. In other words, the smallest segment is 2, the next 3, the next 5, and the back of your hand is 8. By this scale, your fingernail is 1 unit in length. You also have 2 hands, each with 5 digits, and your 8 fingers are each comprised of 3 sections. All Fibonacci numbers! Your hand creates a golden section in relation to your forearm, as the ratio of your forearm to your hand is also 1.618, the Divine Proportion. Furthermore, your hand and forearm together are a golden section in relation to the entire length of your arm.
 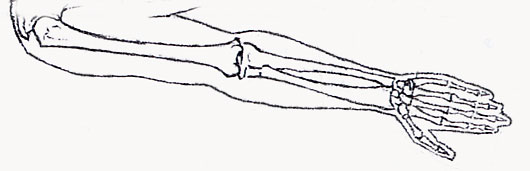
The Human Body
The ventricles of the human heart reset themselves at the Golden Ratio point of the heart's rhythmic cycle.
Leonardo Da Vinci found that the total height of the human body, from toes to top of head, and the height from the toes to the navel depression are in Golden Ratio. Also the height from toes to navel and from the navel to the top of the head are in Golden Ratio. This has been confirmed by measuring 207 students at the Pascal Gymnasium in Munster Germany, where the perfect value of 1.618 was obtained for the first ratio average and 1.619 was obtained for the second. This value held for both girls and boys of similar ages ("Golden Mean of the Human Body" by T. Antony Davis and Rudolf Altevogt).
But there is more. From the top of the head to the bottom of the feet is the body's total height A. From the top of the head to the bottom of the fingertips is a golden section B of the total height A. From the top of the head to the navel and elbows is a golden section C of the golden section B. From the top of the head to the pectorals and armpits, the width of the shoulders, the length of the forearm and shinbone is a golden section D of the golden section C. From the top of the head to the base of the skull and the width of the abdomen is a golden section E of the golden section D. The width of the head and half the width of the chest and the hips is the golden section F of the golden section E.
The human body is also based on the number 5: The torso has 5 appendages, in the arms, legs and head., In turn, each of these has five appendages, in the fingers and toes and 5 openings on the face. and 5 senses in sight, sound, touch, taste and smell. The golden section is also based on 5, as the number phi, or 1.6180339 is computed from the square root of 5 multiplied by .5 plus .5 = Phi.
Relative Planetary Distances
The relative planetary distances average to Phi. The average of the mean orbital distances of each successive planet in relation to the one before it approximates phi: The mean distance is in million kilometers per NASA. If Mercury is 1, these are the relative mean distances Mercury 57.91 (1.00000) Venus 108.21 (1.86859) Earth 149.60 (1.38250) Mars 227.92 (1.52353) Ceres (the largest asteroid) 413.79 (1.81552) Jupiter 778.57 (1.88154) Saturn 1,433.53 (1.84123) Uranus 2,872.46 (2.00377) Neptune 4,495.06 (1.56488) and Pluto 5,869.66 (1.30580) The total is 16.18736 and so if we divide by 10, we get the average which is1.61874. Phi is1.61803.
The Fibonacci Series also predicts accurately the distances of the moons of Jupiter, Saturn and Uranus from each one's respective parent planet. Individual offsets can be attributed to planetary densities. Jupiter has 12 moons. Saturn has 9 moons and Uranus has 5 moons. For actual plotted graphs of these amazing results refer to the Fibonacci Quarterly October 1970, vol. 8, Number 4.
The Greatest Human Achievements Include the Golden Ratio
The dimensions of the King's Chamber of the Great Pyramid in Giza, Egypt are based upon the Golden Ratio. The Great Pyramid's vertical height and the width of any of its sides are in Golden Sections. The architect, Le Corbusier designed his Modulor system around the use of the ratio; the painter Mondrian based most of his work on the Golden Ratio; Leonardo Da Vinci included it in many of his paintings and Claude Debussy used its properties in his music. So did Bela Bartok. The Golden Ratio also is found in widescreen televisions, postcards, credit cards, and photographs which all commonly conform to its proportions. Like the brilliant Pythagoras before him, Leonardo had made an in-depth study of the human figure, showing how all of its major parts were related to the Golden Ratio. The Mona Lisa's face fits inside a perfect Golden Rectangle. The Golden Rectangle is found in his painting called The Last Supper also. Many other Renaissance artists did the same. After Leonardo, artists such as Raphael and Michelangelo made great use of the Golden Ratio to construct their works. Michelangelo's beautiful sculpture of David conforms to the Golden Ratio, from the location of the navel with respect to the height and placement of the joints in the fingers. The builders of the medieval and Gothic churches and cathedrals of Europe also made these structures conform to the Golden Ratio. The Golden Rectangle is one whose sides are in the proportion of the Golden Ratio. This means the longer side is 1.618 times longer than the shorter side. The front of the Parthenon in Athens, Greece can be framed within a Golden Rectangle. Da Vinci's drawing of the Vitruvian Man has the outlines of a rectangle based on the head, one on the torso, and another over the legs.
The Golden Ratio In The Bible
The Ark of the Covenant is a Golden Rectangle. In Exodus 25:10, God commands Moses to build the Ark of the Covenant, in which to hold His Covenant with the Israelites, the Ten Commandments, saying,"Have them make a chest of acacia wood -- two and a half cubits long, a cubit and a half wide, and a cubit and a half high." The ratio of 2.5 to 1.5 is 1.666..., which is as close to phi (1.618 ...) as you can come with such simple numbers and is certainly not visibly different to the eye. The Ark of the Covenant is thus constructed using the Golden Section, or Divine Proportion. This ratio is also the same as 5 to 3, numbers from the Fibonacci series.
Noah's Ark uses a Golden Rectangle. In Genesis 6:15, God commands Noah to build an ark saying,"And this is the fashion which thou shalt make it of: The length of the ark shall be three hundred cubits, the breadth of it fifty cubits, and the height of it thirty cubits."Thus the end of the ark, at 50 by 30 cubits, is also in the ratio of 5 to 3, or 1.666..., again a close approximation of phi not visibly different to the naked eye. Noah's ark was built in the same proportion as ten arks of the covenant placed side by side.
Exodus 27:1-2 mentions the dimensions of the altar -- constructed according to phi: "Build an altar of acacia wood, three cubits high; it is to be square, five cubits long and five cubits wide."
Furthermore, the location of Jerusalem is 31 degrees 45 minutes north of the equator. God said Jerusalem is "the city which I have chosen to put my name there" (1 Kings 11:36). Why did God select this location? First build a rectangular building in Jerusalem with sides that exhibit the golden rectangle ratio. The longer two sides (1.618) must run from east to west. The shorter two sides (1) must run from north to south. Then at each of the four corners place a flag pole. Make the roof flat. Remember that the sun rises in the east and sets in the west. Now if you draw one diagonal line from the northwest to the southeast corner, and another diagonal line from the northeast to southwest corner, you will create angles of 31 degrees 45 minutes with respect to the straight line joining the two southern corners of the building. At the summer solstice, the sun is over the Tropic of Cancer, 23.5 degrees north of the equator. At this point the shadows will point most easterly and westerly. At the winter solstice, the sun is over the Tropic of Capricorn, 23.5 degrees south of the equator. At this point the shadows will point most northerly. On the spring (March 21) and fall (Sept. 23) equinoxes, when the sun is directly over the equator, the shadows created by sunrise and sunset will fall exactly on these diagonal lines. This method can be used at any latitude with rectangles of different proportions. But a rectangle with the proportions of "the golden section " will only give this result at the exact latitude of Jerusalem. It is important to know when the equinoxes occur each year in order to celebrate God's festivals. We are to take the first new moon on or after the spring equinox as New Year's Day. No complex postponement rules or calculated calendar is necessary. Babylon is about one degree further north than Jerusalem. The pyramids of Gizeh are further south and Mecca still further south.

Fibonacci Numbers In The Musical Scale
The musical scales are based on Fibonacci numbers. The piano keyboard scale of C to C has 8 white keys in an "octave" and 5 black keys, making 13 keys total. The 5 black keys are divided into groups: of 2 keys and 3 keys. A scale is comprised of 8 notes, of which the 5th and 3rd notes create the basic foundation of all chords, and are based on whole tone which is 2 steps from the root tone, that is the1st note of the scale. Although there are only 12 notes in the scale, if you don't have a root and octave, a start and an end, you have no means of calculating the gradations in between, so this 13th note as the octave is essential to computing the frequencies of the other notes. The word "octave" comes from the Latin word for 8, referring to the eight whole tones of the complete musical scale, which in the key of C are C-D-E-F-G-A-B-C.
In a scale, the dominant note is the 5th note of the major scale, which is also the 8th note of all 13 notes that comprise the octave. This provides another instance of Fibonacci numbers in key musical relationships. Interestingly, 8/13 is .61538, which approximates phi. What's more, the typical three chord song in the key of A is made up of A, its Fibonacci & phi partner E, and D, to which A bears the same relationship as E does to A. This is analogous to the "A is to B as B is to C" basis for the golden section, or in this case "D is to A as A is to E."
Musical frequencies are based on Fibonacci ratios Notes in the scale of western music have a foundation in the Fibonacci series, as the frequencies of musical notes have relationships based on Fibonacci numbers: A440 Hertz is an arbitrary standard. The American Federation of Musicians accepted the A440 as standard pitch in 1917. It was then accepted by the U.S. government its standard in 1920 and it was not until 1939 that this pitch was accepted internationally. Before recent times a variety of tunings were used. It has been suggested by James Furia and others that A432 be the standard. A432 was often used by classical composers and results in a tuning of the whole number frequencies that are connected to numbers used in the construction of a variety of ancient works and sacred sites, such as the Great Pyramid of Egypt. The controversy over tuning still rages, with proponents of A432 or C256 as being more natural tunings than the current standard. |
|
|
|
|
|
Posted on viernes, 15 de enero de 2010 20:55:47 by truthfinder9
Interesting. From this book (sorry, not all of the formulas converted right):
Mathematical Signatures in Nature: A Sign of Design?
“[The Universe] is written in the language of mathematics, and its characters are triangles, circles, and other geometrical figures, without which it is humanly impossible to understand a single word of it...” – Galileo Galilei1
Math is the universal language, but it is not a human construct. Sure, we create symbols for numbers and mathematical computations, but math itself is more fundamental. 2 + 2 = 4 is universally true, universal in the sense that everywhere in the universe it is true. It does not matter what symbols we create to communicate “2 + 2 = 4” — the equation always remains true. In other words, what we call math is simply a way to describe or visualize the order that is the foundation of the universe’s structure and mechanics.
As we have discussed at length, such order cannot be produced by chance. The level of order is too sophisticated for a random cause. The patterns that are often revealed are too precise. Only intelligence produces such things. Let us look at some of the mathematical constructs that we have uncovered in nature.
Phi [M]
Phi (M = 1.6180339887...) is an irrational number like pi (p = 3.141592653...). Phi and pi are both ratios defined by particular Euclidean geometries, with phi being the division of a line “so that the ratio of the lesser part to the greater part is the same as the ratio of the greater part to the whole.2”
Phi’s abundance in the universe as earned it names such as the Golden Section, the Divine Proportion, the Golden Ratio and the Golden Mean. These names stem from the fact that phi can be found in many natural constructs such as in human and animal proportions (i.e. the arrangement of physical features). Phi relationships can be found in DNA, among the planets of the Solar System (as in Kepler’s Laws), and so on. Even in fractal geometry (used for the irregular geometries found in nature) we find phi in everything from coastlines to crystal formation.
Many argue that phi is also used by humans in such things as art, architecture and music for the balance it produces in designs. However, there are some caveats to this. For example, some claim one can find phi — not surprisingly — in the structure or design of the pyramids. Is phi intentional in the pyramids or merely the result of what is good geometrical design? It is probably the latter. Architecture is often designed with balance and stability which necessitates geometries that contain phi, though these geometries are not always necessary. Phi may be intentional in some structures, but it is accidental or inadvertent in others.
While there is always an amount of subjectivity in how one designs a structure, there is much more of this in artwork. Phi can be seen in certain art pieces, but many more do not exhibit phi. Art that uses geometry as a basis will naturally converge on phi (with phi not necessarily “encoded” in the painting by the artist). We can purposely incorporate phi or inadvertently do so through our use of the geometries we have discovered.
Either way we (intelligent designers) are using precise constructs. How do such precise relations appear repeatedly in nature?
Fibonacci Series
This is the Fibonacci series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34. . .etc. It is very simply explained as each number in the series being the sum of the previous two numbers. The ratio of each successive pair of numbers (starting with 3/2) in the series approximates phi (i.e. 8 divided by 5 is 1.6). The accuracy of these ratios’ approximations to phi increases considerably as you go through the series. Phi can also be used to estimate any number in the Fibonacci series: fn = Mn / 5½.
Why is this important? Because the Fibonacci series precisely describes the spiral patterns common in nature: In shells, hurricanes, whirlpools, spiral galaxies, DNA and plant life. Phi is all around us. For example: The ratio of scales in the opposing spirals around a pine cone is 5:8; bumps on a pineapple are 8:13; seeds in a sunflower are 21:34. All of these ratios are adjacent pairs in the Fibonacci series.
Biblical Indications of Phi?
Exodus 25:10 writes: “Have them make a chest of acacia wood — two and a half cubits long, a cubit and a half wide, and a cubit and a half high.” Here we find that “The ratio of 2.5 to 1.5 is 1.666..., which is as close to phi (1.618...) as you can come with such simple numbers and is certainly not visibly different to the eye. The Ark of the Covenant is thus constructed using the Golden Section, or Divine Proportion. This ratio is also the same as 5 to 3, numbers from the Fibonacci series.3”
God instructed Noah in Genesis 6:15 to build an ark this way: “This is how you are to build it: The ark is to be 450 feet long, 75 feet wide and 45 feet high.” Hence, 75 by 45 feet is also in the ratio of 5 to 3, or 1.666..., another “close approximation of phi not visibly different to the naked eye. Noah’s ark was built in the same proportion as ten arks of the covenant placed side by side.4”
These indications of phi may or may not have been intentional. However, they are more evidence of a trend for man to use the same logic embedded in the universe. As Gary Meisner writes, “The pervasive appearance of phi throughout life and the universe is believed by some to be the signature of God, a universal constant of design used to assure the beauty and unity of His creation.5”
Pi [p]
Pi is the ratio of the circumference of a circle to its diameter (p = 3.141592653...). Pi is just as fundamental as phi in the universe, but because it is more familiar, its presence does not seem as startling. Yet mathematicians have spent millennia computing its numbers and looking for patterns in the pi sequence. Perhaps not surprisingly, pi can be related to phi. One way is through trigonometric relations: 2 H cos (p / 5) = M and 2 H sin (p / 5) = Ö(3 - M). There are other relations as well.6
Pi in the Bible?
1 Kings 7:23 writes: “He made the Sea of cast metal, circular in shape, measuring ten cubits from rim to rim and five cubits high. It took a line of thirty cubits to measure around it.” We know that circumference equals pi times diameter (c = pd). So from 1 Kings 7:23 we produce 30 = p10. Solving for p we get 3. Since p actually equals 3.141592653..., some people reason that the Bible is wrong. Is it?
First we must recognize that the Bible commonly uses rounded figures. These are descriptions, not architectural blueprints. Secondly, it has been shown by some that since the Hebrew does not have digits — all letters are also numbers — the relevant Hebrew in this passage can be calculated to find pi.7 The calculation comes out to 3.14150943... This is only a difference of 0.0000832 with actual pi, making the Bible’s description of pi the most accurate in antiquity.
Perhaps the Hebrews did not specifically calculate pi, but they managed to come very close “accidentally.” Another caveat is that many have tried to abuse the Hebrew and find endless “codes” hidden in the Bible. It can be shown how and why these codes are nonexistent8 or at least cannot be attributed the variety of meanings that some people claim the codes produce. While certain numbers, sequences, etc., in the Bible and elsewhere have been attributed particular meanings and usages, there is a big difference between what can be defined as pseudoscientific numerologies and scientific patterns. The latter are constant and repeatable (pi and phi) the former are inconsistent and variable (“Bible codes”).
Universal Language
So it seems mathematical patterns are inherent to the very structure of the universe. While we use our language of mathematics to describe these patterns and all of the precise fine-tuning found in the universe, the mathematical ratios themselves seem to be design evidences: A universal language, unchanging throughout time or place; too precise and nonnrandom to be products of chance.
We have also seen how biblical writings show examples of these mathematical constructs, both in usage and understanding. Once again the Bible shows a level of knowledge and accuracy that matches and surpasses other cultures contemporary to the Hebrews.
1. Mario Livio, The Golden Ratio (New York, NY: Broadway, 2003), pp. 241-242.
2. Miranda Lundy, Sacred Geometry (New York. NY: Walker, 1998), pp. 24-25.
For more on how phi is defined, see the websites “Phi: The Golden Number” at www.goldennumber.net by Gary Meisner, “The Golden section ratio: Phi” at www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/phi.html by Ron Knott and “Phi: That Golden Number” at jwilson.coe.uga.edu/emt669/Student.Folders/Frietag.Mark/Homepage/Goldenratio/goldenratio.html by Mark Freitag.
3. - 5. Gary Meisner’s “Phi in the Bible” at goldennumber.net/bible.htm.
6. Gary Meisner, “Pi, Phi and Fibonacci Numbers” at goldennumber.net/pi-phi-fibonacci.htm. More on the Fibonacci series in Ron Knott’s “Fibonacci Numbers and the Golden Section” at www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fib.html.
7. Jochen Katz, “Pi in the Bible” at answering-islam.org.uk/Religions/Numerics/pi.html.
8. Randall Ingermanson, Who Wrote the Bible Code? A Physicist Probes the Current Controversy. Colorado Springs, Colorado: Waterbook, 1999. The author maintains additional information and appendices to his book on-line at www.rsingermanson.com. More on the Bible codes can be found at www.reasons.org/resources/apologetics/biblecode.shtml?main and at www.answering-islam.org.uk/Religions/Numerics/.
http://www.freerepublic.com/focus/f-religion/2429476/posts |
|
|
|
|
The Fibonacci Sequence
Studied along time ago, God's numbers.People love to leave God out of these numbers,study the human body-ALL PROPORTIONS ARE GODS NUMBERS.Fingers, to toes, to nose.A starter;
Another notable example is human body.In human body, the ratio of the length of forearm to the length of the hand is equal to 1.618, that is, Golden Ratio. Another well-known examples on human body are:
The ratio between the length and width of face
Ratio of the distance between the lips and where the eyebrows meet to the length of nose
Ratio of the length of mouth to the width of nose
Ratio of the distance between the shoulder line and the top of the head to the head length
Ratio of the distance between the navel and knee to the distance between the knee and the end of the foot
Ratio of the distance between the finger tip and the elbow to the distance between the wrist and the elbow
Read more: http://scienceray.com/mathematics/th...#ixzz0vyU32DdS
---------------------
Fibonacci Numbers and Nature
This page has been split into TWO PARTS.
This, the first, looks at the Fibonacci numbers and why they appear in various "family trees" and patterns of spirals of leaves and seeds.
The second page then examines why the golden section is used by nature in some detail, including animations of growing plants.
http://www.maths.surrey.ac.uk/hosted...ci/fibnat.html
---------------------------------------------------------
The Human Head
Human beauty is based on the Divine Proportion. Many experiments have been carried out to prove that the proportions of the top models' faces conform more closely to the Golden Ratio than the rest of the population. The human face is based entirely on Phi .The head forms a golden rectangle with the eyes at its midpoint. The mouth and nose are each placed at golden sections of the distance between the eyes and the bottom of the chin. The ear reflects the shape of a Fibonacci spiral. Even the dimensions of our teeth are based on phi. The front two incisor teeth form a golden rectangle, with a phi ratio in the heighth to the width. The ratio of the width of the first tooth to the second tooth from the center is also phi. The ratio of the width of the smile to the third tooth from the center is phi as well.
The Human Finger Joints and Hand
Each segment of each finger, from the tip to the base of the wrist, is larger than the preceding one by about the Fibonacci ratio of 1.618. In other words, the smallest segment is 2, the next 3, the next 5, and the back of your hand is 8. By this scale, your fingernail is 1 unit in length. You also have 2 hands, each with 5 digits, and your 8 fingers are each comprised of 3 sections. All Fibonacci numbers! Your hand creates a golden section in relation to your forearm, as the ratio of your forearm to your hand is also 1.618, the Divine Proportion. Furthermore, your hand and forearm together are a golden section in relation to the entire length of your arm.
The Human Body
The ventricles of the human heart reset themselves at the Golden Ratio point of the heart's rhythmic cycle.
Leonardo Da Vinci found that the total height of the human body, from toes to top of head, and the height from the toes to the navel depression are in Golden Ratio. Also the height from toes to navel and from the navel to the top of the head are in Golden Ratio. This has been confirmed by measuring 207 students at the Pascal Gymnasium in Munster Germany, where the perfect value of 1.618 was obtained for the first ratio average and 1.619 was obtained for the second. This value held for both girls and boys of similar ages ("Golden Mean of the Human Body" by T. Antony Davis and Rudolf Altevogt).
But there is more. From the top of the head to the bottom of the feet is the body's total height A. From the top of the head to the bottom of the fingertips is a golden section B of the total height A. From the top of the head to the navel and elbows is a golden section C of the golden section B. From the top of the head to the pectorals and armpits, the width of the shoulders, the length of the forearm and shinbone is a golden section D of the golden section C. From the top of the head to the base of the skull and the width of the abdomen is a golden section E of the golden section D. The width of the head and half the width of the chest and the hips is the golden section F of the golden section E.
The human body is also based on the number 5: The torso has 5 appendages, in the arms, legs and head., In turn, each of these has five appendages, in the fingers and toes and 5 openings on the face. and 5 senses in sight, sound, touch, taste and smell. The golden section is also based on 5, as the number phi, or 1.6180339 is computed from the square root of 5 multiplied by .5 plus .5 = Phi.
Relative Planetary Distances
The relative planetary distances average to Phi. The average of the mean orbital distances of each successive planet in relation to the one before it approximates phi: The mean distance is in million kilometers per NASA. If Mercury is 1, these are the relative mean distances Mercury 57.91 (1.00000) Venus 108.21 (1.86859) Earth 149.60 (1.38250) Mars 227.92 (1.52353) Ceres (the largest asteroid) 413.79 (1.81552) Jupiter 778.57 (1.88154) Saturn 1,433.53 (1.84123) Uranus 2,872.46 (2.00377) Neptune 4,495.06 (1.56488) and Pluto 5,869.66 (1.30580) The total is 16.18736 and so if we divide by 10, we get the average which is1.61874. Phi is1.61803.
The Fibonacci Series also predicts accurately the distances of the moons of Jupiter, Saturn and Uranus from each one's respective parent planet. Individual offsets can be attributed to planetary densities. Jupiter has 12 moons. Saturn has 9 moons and Uranus has 5 moons. For actual plotted graphs of these amazing results refer to the Fibonacci Quarterly October 1970, vol. 8, Number 4.
The Greatest Human Achievements Include the Golden Ratio
The dimensions of the King's Chamber of the Great Pyramid in Giza, Egypt are based upon the Golden Ratio. The Great Pyramid's vertical height and the width of any of its sides are in Golden Sections. The architect, Le Corbusier designed his Modulor system around the use of the ratio; the painter Mondrian based most of his work on the Golden Ratio; Leonardo Da Vinci included it in many of his paintings and Claude Debussy used its properties in his music. So did Bela Bartok. The Golden Ratio also is found in widescreen televisions, postcards, credit cards, and photographs which all commonly conform to its proportions. Like the brilliant Pythagoras before him, Leonardo had made an in-depth study of the human figure, showing how all of its major parts were related to the Golden Ratio. The Mona Lisa's face fits inside a perfect Golden Rectangle. The Golden Rectangle is found in his painting called The Last Supper also. Many other Renaissance artists did the same. After Leonardo, artists such as Raphael and Michelangelo made great use of the Golden Ratio to construct their works. Michelangelo's beautiful sculpture of David conforms to the Golden Ratio, from the location of the navel with respect to the height and placement of the joints in the fingers. The builders of the medieval and Gothic churches and cathedrals of Europe also made these structures conform to the Golden Ratio. The Golden Rectangle is one whose sides are in the proportion of the Golden Ratio. This means the longer side is 1.618 times longer than the shorter side. The front of the Parthenon in Athens, Greece can be framed within a Golden Rectangle. Da Vinci's drawing of the Vitruvian Man has the outlines of a rectangle based on the head, one on the torso, and another over the legs.
The Golden Ratio In The Bible
The Ark of the Covenant is a Golden Rectangle. In Exodus 25:10, God commands Moses to build the Ark of the Covenant, in which to hold His Covenant with the Israelites, the Ten Commandments, saying,"Have them make a chest of acacia wood -- two and a half cubits long, a cubit and a half wide, and a cubit and a half high." The ratio of 2.5 to 1.5 is 1.666..., which is as close to phi (1.618 ...) as you can come with such simple numbers and is certainly not visibly different to the eye. The Ark of the Covenant is thus constructed using the Golden Section, or Divine Proportion. This ratio is also the same as 5 to 3, numbers from the Fibonacci series.
Noah's Ark uses a Golden Rectangle. In Genesis 6:15, God commands Noah to build an ark saying,"And this is the fashion which thou shalt make it of: The length of the ark shall be three hundred cubits, the breadth of it fifty cubits, and the height of it thirty cubits."Thus the end of the ark, at 50 by 30 cubits, is also in the ratio of 5 to 3, or 1.666..., again a close approximation of phi not visibly different to the naked eye. Noah's ark was built in the same proportion as ten arks of the covenant placed side by side.
Exodus 27:1-2 mentions the dimensions of the altar -- constructed according to phi: "Build an altar of acacia wood, three cubits high; it is to be square, five cubits long and five cubits wide."
Furthermore, the location of Jerusalem is 31 degrees 45 minutes north of the equator. God said Jerusalem is "the city which I have chosen to put my name there" (1 Kings 11:36). Why did God select this location? First build a rectangular building in Jerusalem with sides that exhibit the golden rectangle ratio. The longer two sides (1.618) must run from east to west. The shorter two sides (1) must run from north to south. Then at each of the four corners place a flag pole. Make the roof flat. Remember that the sun rises in the east and sets in the west. Now if you draw one diagonal line from the northwest to the southeast corner, and another diagonal line from the northeast to southwest corner, you will create angles of 31 degrees 45 minutes with respect to the straight line joining the two southern corners of the building. At the summer solstice, the sun is over the Tropic of Cancer, 23.5 degrees north of the equator. At this point the shadows will point most easterly and westerly. At the winter solstice, the sun is over the Tropic of Capricorn, 23.5 degrees south of the equator. At this point the shadows will point most northerly. On the spring (March 21) and fall (Sept. 23) equinoxes, when the sun is directly over the equator, the shadows created by sunrise and sunset will fall exactly on these diagonal lines. This method can be used at any latitude with rectangles of different proportions. But a rectangle with the proportions of "the golden section " will only give this result at the exact latitude of Jerusalem. It is important to know when the equinoxes occur each year in order to celebrate God's festivals. We are to take the first new moon on or after the spring equinox as New Year's Day. No complex postponement rules or calculated calendar is necessary. Babylon is about one degree further north than Jerusalem. The pyramids of Gizeh are further south and Mecca still further south.
Fibonacci Numbers In The Musical Scale
The musical scales are based on Fibonacci numbers. The piano keyboard scale of C to C has 8 white keys in an "octave" and 5 black keys, making 13 keys total. The 5 black keys are divided into groups: of 2 keys and 3 keys. A scale is comprised of 8 notes, of which the 5th and 3rd notes create the basic foundation of all chords, and are based on whole tone which is 2 steps from the root tone, that is the1st note of the scale. Although there are only 12 notes in the scale, if you don't have a root and octave, a start and an end, you have no means of calculating the gradations in between, so this 13th note as the octave is essential to computing the frequencies of the other notes. The word "octave" comes from the Latin word for 8, referring to the eight whole tones of the complete musical scale, which in the key of C are C-D-E-F-G-A-B-C.
In a scale, the dominant note is the 5th note of the major scale, which is also the 8th note of all 13 notes that comprise the octave. This provides another instance of Fibonacci numbers in key musical relationships. Interestingly, 8/13 is .61538, which approximates phi. What's more, the typical three chord song in the key of A is made up of A, its Fibonacci & phi partner E, and D, to which A bears the same relationship as E does to A. This is analogous to the "A is to B as B is to C" basis for the golden section, or in this case "D is to A as A is to E."
Musical frequencies are based on Fibonacci ratios Notes in the scale of western music have a foundation in the Fibonacci series, as the frequencies of musical notes have relationships based on Fibonacci numbers: A440 Hertz is an arbitrary standard. The American Federation of Musicians accepted the A440 as standard pitch in 1917. It was then accepted by the U.S. government its standard in 1920 and it was not until 1939 that this pitch was accepted internationally. Before recent times a variety of tunings were used. It has been suggested by James Furia and others that A432 be the standard. A432 was often used by classical composers and results in a tuning of the whole number frequencies that are connected to numbers used in the construction of a variety of ancient works and sacred sites, such as the Great Pyramid of Egypt. The controversy over tuning still rages, with proponents of A432 or C256 as being more natural tunings than the current standard.
Musical compositions often reflect Fibonacci numbers and phi Fibonacci and phi relationships are often found in the timing of musical compositions. As an example, the climax of songs is often found at roughly the phi point (61.8%) of the song, as opposed to the middle or end of the song. In a 32 bar song, this would occur in the 20th bar.
If you'd like to know more, we publish a 32-page booklet called Who Is The Scarlet Harlot of Babylon? ($3.00). Use this link to pay with a credit card:
- US orders ($0.50 shipping)
- Canada/Mexico orders ($0.60 shipping)
http://www.goldismoney2.com/showthread.php?7277-The-Fibonacci-Sequence
|
|
|
|
|

from Mid-Atlantic Geomancy
If we want to talk with God/dess, experience has shown that it helps to be in the right environment. Spiritual seekers from Mayans through Christians, Native Americans, Egyptians and Hindus to the Neolithic builders of the stone rings in Britain and Ireland (and many more) found that by constructing their sacred places using certain geometrical ratios - just a small handful of them - they could more easily connect with their Maker.
Yes, it is possible to speak with our Creator anytime. However, sacred geometry makes this easier, and different ratios make different connections easier. The ratios have to do with different spiritual activities like healing, foretelling the future, long-distance communication, levitation and, most important, heightened ability to communicate with our Maker. These ratios help us to vibrate at the appropriate frequency to aid us in accomplishing the particular spiritual activity we have in mind.
Nearly every ancient archaeological site predating recorded history, from the Pyramids of Egypt and Mexico, to Stonehenge and beyond, employs mysterious mathematical alignments throughout their design.
These architectural formulas, rarely used today, are considered sacred and have also been found in the way they're arranged relation to each other and, most inexplicably, in the Monuments of Cydonia, and the Face on Mars.
When one looks at sacred enclosures globally, there is a group of five mathematical ratios that are found all over the world from Japan's pagodas to Mayan temples in the Yucatan, and from Stonehenge to the Great Pyramid. These ratios are:
-
Square Root of Two = 1.414...
-
Square Root of Three = 1.732...
-
Square Root of Five = 2.236...
-
Phi = 1.618...
Phi is the Golden Section of the Greeks. It was said to be the first section in which the One became many.
-
Pi = 3.1416...
Pi is found in any circle. If the diameter is 1, the circumference is 3.1416 (C = D).
These are all irrational numbers. Pi can be taken to 1500 decimal places with no discernable pattern to it (is that Chaos?). Let's take a closer look at each of these special numbers, and see how we can find them in the sacred geometry used by geomancers around the world. All five of these numbers gain their meaning only when beaten against the One. They are all ratios of x:1. The One is where it begins.
Pi - 3.1416 : 1 - the Circle
|
Pi (3.1416 : 1) is found in any circle. In sacred geometry, the circle represents the spiritual realms.
A circle, because of that transcendental number pi, cannot be described with the same degree of accuracy as the physical square.
The circle is yin.
It is a good shape to do all kinds of spiritual activities in. It is good for groups to work in circles. There are many examples of sacred spaces that are circular.
|
The Circle:
Radius (CD) = 1
Diameter (AB) = 2
Circumference = pi (3.1416) x Diameter
|
|

Ring of Brodgar, Mainland Orkney.
|
Most stone rings in the British isles are not actually circular.
Dr Alexander Thom proved this with his pioneering work in the sixties.
Some of the true circles are Merry Maidens in Cornwall, Stonehenge and the Ring of Brodgar.
|
Square Root of Two - 1.414 : 1 - the Square
|
In sacred geometry, the square represents the physical world.
It can be defined totally.
If its side is one, its perimeter is exactly four, and its area is one square - exactly.
The Square is yang.
|
The Square Side (AB) = 1
Diagonal (AC) = Square Root of Two, 1.414
|
|
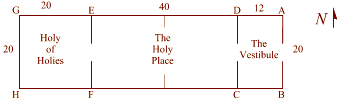
The Square Side (AB) = 1
Diagonal (AC) = Square Root of Two, 1.414
|
The square was found was in the Holy of Holies (the back room) of Solomon's Temple (G,H,F,E).
This was where the Hebrews kept the Ark of the Covenant and other most sacred treasures. (The dimensions here are taken from the first part of the Ezekiel Chapter 41.)
|
|
On top of if(screen) { topPos=0; leftPos=0; } // Open full page // // Open to size // var newWin1=null; function getPage(thePage,wt,ht) { leftPos= (screen.width-wt)/2; topPos = (screen.height-ht)/2; if ( newWin1 && !newWin1.closed ) { newWin1.close(); } newWin1 = window.open(thePage,'aWin','toolbars=no, resizeable=no,scrollbars=no,left='+leftPos+',top='+topPos+',width='+wt+',height='+ht); } // -->Glastonbury Tor sits an impressive stone tower.
The Tor and its tower dominate the if(screen) { topPos=0; leftPos=0; } // Open full page // // Open to size // var newWin1=null; function getPage(thePage,wt,ht) { leftPos= (screen.width-wt)/2; topPos = (screen.height-ht)/2; if ( newWin1 && !newWin1.closed ) { newWin1.close(); } newWin1 = window.open(thePage,'aWin','toolbars=no, resizeable=no,scrollbars=no,left='+leftPos+',top='+topPos+',width='+wt+',height='+ht); } // -->Somerset Levels .
This is a view taken from inside the tower looking upward.

|

|
Square Root of Three - 1.732 : 1 - Vesica Pisces
The Vesica Pisces is created by two identical intersecting circles, the circumference of one intersecting the center of the other. The vulva-shaped space thus created is called the Vesica Pisces.
|
|
The Vesica Pisces:
Two Circles share a common radius (AB).
Radius AB = 1
The intersecting circles create a Vesica Pisces.
The minor axis of this Vesica Pisces (AB) = 1,
The major axis (CD) = the square root of three, 1.732
|
CB = AB
|
=
|
1 ..... Therefore:
|
|
a² + b²
|
=
|
c²
|
|
.5² + x²
|
=
|
1²
|
|
x²
|
=
|
.75
|
|
 2 2
|
=
|
 .75 .75
|
|
x
|
=
|
.8660 = CE
|
|
CE is 1/2 of the major axis CD
|
|
2 CE
|
=
|
CD
|
|
.8660 * 2
|
=
|
CD
|
|
CD
|
=
|
1.7320 = 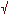 3 3
|
|
|
This is the lid of the if(screen) { topPos=0; leftPos=0; } // Open full page // // Open to size // var newWin1=null; function getPage(thePage,wt,ht) { leftPos= (screen.width-wt)/2; topPos = (screen.height-ht)/2; if ( newWin1 && !newWin1.closed ) { newWin1.close(); } newWin1 = window.open(thePage,'aWin','toolbars=no, resizeable=no,scrollbars=no,left='+leftPos+',top='+topPos+',width='+wt+',height='+ht); } // -->Chalice Well designed by Bligh Bond in the early part of this century.
It covers one of the most powerful Holy Wells in Britain.
The Chalice Well has numerous examples of vesicas.
|

|
|

Gothic arch on the tower on the Glastonbury Tor. This site was a hermitage and retreat for early Christian monks
|

Gothic arch in Gallilee of Glastonbury Abbey. Note circular Romanesque arches behind in the Mary Chapel.
|
The top half of the Vesica Pisces is the Gothic Arch - see if(screen) { topPos=0; leftPos=0; } // Open full page // // Open to size // var newWin1=null; function getPage(thePage,wt,ht) { leftPos= (screen.width-wt)/2; topPos = (screen.height-ht)/2; if ( newWin1 && !newWin1.closed ) { newWin1.close(); } newWin1 = window.open(thePage,'aWin','toolbars=no, resizeable=no,scrollbars=no,left='+leftPos+',top='+topPos+',width='+wt+',height='+ht); } // -->Chartres Cathedral .
It is the sacred geometric shape of the Piscean Age.
|
Square Root of Five - 2.236 : 1 - the Double Square
|
The Double Square is found in some of the best known sacred spaces in the world, from the King's Chamber in the Great Pyramid and Solomon's Temple in the Bible to the interior of if(screen) { topPos=0; leftPos=0; } // Open full page // // Open to size // var newWin1=null; function getPage(thePage,wt,ht) { leftPos= (screen.width-wt)/2; topPos = (screen.height-ht)/2; if ( newWin1 && !newWin1.closed ) { newWin1.close(); } newWin1 = window.open(thePage,'aWin','toolbars=no, resizeable=no,scrollbars=no,left='+leftPos+',top='+topPos+',width='+wt+',height='+ht); } // -->Calendar II, an important underground stone chamber in Vermont, USA.
The diagonal of a double square is to the shorter side as the square root of five is to one.
The square root of five = .618 + 1 + .618.
|
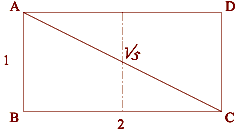
The Double Square:
Short Side = 1
Longer Side = 2
Diagonal = Square Root of Five, 2.236
|
|
(ABCD) Double Square in Solomons Temple
|
if(screen) { topPos=0; leftPos=0; } // Open full page // // Open to size // var newWin1=null; function getPage(thePage,wt,ht) { leftPos= (screen.width-wt)/2; topPos = (screen.height-ht)/2; if ( newWin1 && !newWin1.closed ) { newWin1.close(); } newWin1 = window.open(thePage,'aWin','toolbars=no, resizeable=no,scrollbars=no,left='+leftPos+',top='+topPos+',width='+wt+',height='+ht); } // -->Solomons temple provides numerous examples of sacred geometry.
The holy place (EFCD) is the place where good Jews who had been properly cleansed could go.
This space measures twenty cubits by forty cubits.
|
Another place where a double square is found is the Calendar II underground chamber site in central Vermont in the USA. It measures ten feet by twenty feet.
|

.
Calendar II, a drystone walled underground stone chamber in central Vermont, USA.
|

The interior of the chamber is 20 feet long by 10 feet wide , or 2 to 1. The chamber is oriented towards the Winter Solstice Sunrise.
|
Phi - 1.618:1 - Ø - the Phi Rectangle
|
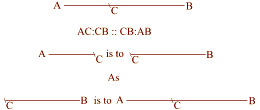
The Golden Section, Phi, 1.618:
The shorter section on the right = 3
The longer section = 5
The shorter is to the longer
as the longer is to the whole
3:5 : : 5:8
|
In the Beginning was the One. In order to observe itself, it cut part of itself away to make 'Other'. This Golden Section is in beautiful proportion. As the subdividing continued away from the One, they continued in this phi ratio.
This can be used to go back to the One as well. It is in this sense that three is farther away from the One than two is.
Have you ever noticed that it is easier mathematically to go away from One than to go towards it? In other words, it is easier to add and multiply than it is to subtract and divide.
|
3:5 : : 5:8. This ratio indicates that it is part of this series: 1 . 2 . 3 . 5 . 8 . 13 . 21 . 34 . 55 . 89, and so on. This is called the Fibonacci Series. Start anywhere in the series, add the number below, and you get the next number (for example, 21 + 13 = 34). As one ascends up the series, any number in the series, when divided into the next one up, gets closer and closer to (but never hits exactly) 1.618, phi, the Golden Section.
|
On a line create square
(ABCD) where AB = 1
|
|
|
Divide lines (AD) and (BC) in half
at (F) and (E). (BC) = 1, (EC) = .5
Double square (ECDF) is thus
created with a diameter of (ED).
|
|
|
Using (ED) as a radius
swing arc from (D) downwards to 0
intersect the initial base line at (G).
Extend line (AFD), and create a
perpendicular to line (BECG) at (G)
so that it intersects line (AFD) at (H),
thus creating phi rectangle (ABGH).
|
|
|
The formula that shows this is:
Phi = ( 1 + square root of 5 ) divided by 2
(BE) = 1/2
(ED) = 5/2
.5 + 1.118 = 1.618
|
|
Extend arc (DG) through (A) to (I).
|
|
|
|
 Primer Primer
 Anterior
21 a 35 de 170
Siguiente Anterior
21 a 35 de 170
Siguiente Último
Último
|
 I have long been fascinated by the phenomena of phi (Greek letter), the Fibonacci number series, and the Divine proportion, Golden Proportion, Golden mean, Golden ratio, Golden spiral, Golden rectangle. To me this is such a clear evidence of God’s existence and His mighty genius in the creation of all things in nature. If you’ve never heard of this, look into it – you will be amazed! But here are some facts and examples to get you started.
I have long been fascinated by the phenomena of phi (Greek letter), the Fibonacci number series, and the Divine proportion, Golden Proportion, Golden mean, Golden ratio, Golden spiral, Golden rectangle. To me this is such a clear evidence of God’s existence and His mighty genius in the creation of all things in nature. If you’ve never heard of this, look into it – you will be amazed! But here are some facts and examples to get you started. In mathematics, the Fibonacci series are the numbers in the following sequence of integers:
In mathematics, the Fibonacci series are the numbers in the following sequence of integers: A Nautilis seashell is one of the most exquisite examples of the divine proportion.
A Nautilis seashell is one of the most exquisite examples of the divine proportion. Plants with spiral patterns related to the golden angle also display another curious mathematical property. The seeds of a flower head form interlocking spirals in both clockwise and counterclockwise directions. The number of clockwise spirals differs from the number of counterclockwise spirals, and these two numbers are called the plant’s parastichy numbers (pronounced pi-RAS-tik-ee or PEHR-us-tik-ee). These numbers have a remarkable consistency. They are almost always two consecutive Fibonacci numbers.
Plants with spiral patterns related to the golden angle also display another curious mathematical property. The seeds of a flower head form interlocking spirals in both clockwise and counterclockwise directions. The number of clockwise spirals differs from the number of counterclockwise spirals, and these two numbers are called the plant’s parastichy numbers (pronounced pi-RAS-tik-ee or PEHR-us-tik-ee). These numbers have a remarkable consistency. They are almost always two consecutive Fibonacci numbers.

 Note: This program is made available by Michael Semprevivo for free for non-commercial use only. The PhiBar.exe program was scanned with Norton’s Antivirus program on 03/01/2003 using current virus definitions and found to be virus free but no express or implied warranties are given with respect to its use.
Note: This program is made available by Michael Semprevivo for free for non-commercial use only. The PhiBar.exe program was scanned with Norton’s Antivirus program on 03/01/2003 using current virus definitions and found to be virus free but no express or implied warranties are given with respect to its use. The Fibonacci series appears in the foundation of aspects of art, beauty and life. Even music has a foundation in the series, as:
The Fibonacci series appears in the foundation of aspects of art, beauty and life. Even music has a foundation in the series, as:




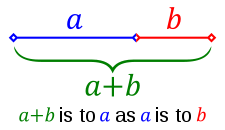
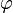


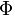









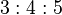















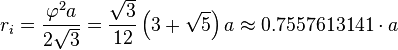

 (also called
(also called 



 If we join mid-points of the dodecahedron's faces, we can get three rectangles all at right angles to each other. What's more, they are Golden Rectangles since their edges are in the ratio 1 to Phi.
If we join mid-points of the dodecahedron's faces, we can get three rectangles all at right angles to each other. What's more, they are Golden Rectangles since their edges are in the ratio 1 to Phi.