|
|
General: BODAS DE CANA (CONVERSION DEL AGUA EN VINO)=GRIAL=CESAR=SATURNO=CRONO
إختار ملف آخر للرسائل |
|
جواب |
رسائل 1 من 83 في الفقرة |
|
CESAREA DE FILIPO (CLAVE CESAR / SATURNO / CRONO EN EL CONTEXTO A LA TRANSFIGURACION)
SHABBAT = CESAR DEL TRABAJO
BODAS DE CANA= SEPTIMO / OCTAVO DIA
CESAR = CLAVE SABATICA
1. Génesis 8:22: Mientras la tierra permanezca, no CESARán la sementera y la siega, el frío y el calor, el verano y el invierno, y el día y la noche.
2. Éxodo 5:4: Entonces el rey de Egipto les dijo: Moisés y Aarón, ¿por qué hacéis CESAR al pueblo de su trabajo? Volved a vuestras tareas.
3. Éxodo 5:5: Dijo también Faraón: He aquí el pueblo de la tierra es ahora mucho, y vosotros les hacéis CESAR de sus tareas.
|
|
|
|
جواب |
رسائل 69 من 83 في الفقرة |
|
ESTO ES LO QUE SIGNIFICA "DESCUBRIR LA DESNUDEZ"
Por Tito Martínez
"La desnudez del hermano de tu padre no descubrirás; a su esposa no te acercarás; tu tía es
ella" (Lev.18:14).
"Si un hombre se acuesta con la mujer de su padre, la 'desnudez de su padre' habrá
descubierto" (Lev. 20:11)
"Si un hombre toma a la mujer de su hermano, es cosa impura; la 'desnudez de su hermano' habrá descubierto" (Lev.20:21).
Ahí lo tenemos bien claro, descubrir la desnudez de alguien, especialmente de un pariente, significa tener relaciones sexuales con ese pariente. Esto no tiene que ver nada con ver a alguien en pelotas. Decir que mirar a alguien en pelotas es un pecado, es de idiotas mentales, es una total falsedad. ¡¡El pecado es tener relaciones sexuales con tu tia, tu nuera, tu madre, tu madrastra, tu cuñada, tu hermana!!. Pero es totalmente falso decir que ver a alguien desnudo o desnuda es pecado.
Fijaos bien lo que dice Levítico 20:11, dice bien clarito que descubrir la desnudez de tu padre significa ACOSTARTE CON LA ESPOSA DE TU PADRE, es decir, con tu madre. Cuando el Génesis dice que Cam vio o descubrió la desnudez de su padre Noé, lo que significa sencillamente es que Cam SE ACOSTÓ CON SU MADRE, y de esa relación incestuosa nació Canaán, por eso es que Dios maldijo a Canaán, porque era el hijo de ese incesto.
genial mensaje de TITO MARTINEZ
|
|
|
|
جواب |
رسائل 70 من 83 في الفقرة |
|
|
Si hablas de las victimas del holocausto judío..
Todo ese sacrificio no fue en vano..
Israel consolidó su soberanía....
En el sufrimiento y en la sangre de todas esas víctimas..
Cómo que no hay justicia ?
Saludos
El Ungido
|
|
|
|
|
|
|
|
| De: Rolmen |
Enviado: 18/10/2018 11:35 |
|
Ya veo, el silencio es elocuente...hechos y no palabras, mejor iré a conversar con la madre naturaleza...
|
|
|
|
|
| De: Rolmen |
Enviado: 18/10/2018 11:39 |
|
|
|
|
| De: Rolmen |
Enviado: 18/10/2018 11:43 |
|
|
|
|
| De: Rolmen |
Enviado: 18/10/2018 11:46 |
|
|
|
|
| De: Rolmen |
Enviado: 18/10/2018 11:51 |
|
|
|
|
| De: Rolmen |
Enviado: 18/10/2018 12:01 |
|
|
|
|
| De: Rolmen |
Enviado: 18/10/2018 12:02 |
|
|
|
|
| De: Rolmen |
Enviado: 18/10/2018 12:03 |
|
|
|
|
|
|
|
|
|
جواب |
رسائل 71 من 83 في الفقرة |
|
|
|
|
جواب |
رسائل 72 من 83 في الفقرة |
|
|
|
22/7=3.14=PI
12 PUNTOS EN SU CIRCUNFERENCIA=RELOJ=SANTA CENA
LONGITUD CIRCUNFERENCIA=PIxDIAMETRO
 |
|
|
|
|
|
|
|
|
|
جواب |
رسائل 73 من 83 في الفقرة |
|
ISLA SAN GIORGIO (VENECIA)=GEORGE LEMAITRE
GEMATRIA EN INGLES DE SEED=33
GEMATRIA EN INGLES DE GATE=33
SARA (CE-SAREA DE FILIPO)=PARALELO 33
 the Apple
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|

|
|
|
|
جواب |
رسائل 74 من 83 في الفقرة |
|
|
|
Hércules (constelación)
De Wikipedia, la enciclopedia libre
Recibe su nombre del héroe mitológico, Hércules y es la quinta en tamaño de las 88 constelaciones modernas. También era una de las 48 constelaciones de Ptolomeo.
[editar] Características destacables
No tiene estrellas de primera magnitud, siendo la más brillante β Herculis con magnitud 2,78. μ Herculis se encuentra a 27,4 años luz de la Tierra. El Ápex solar (punto del cielo que indica la dirección hacia la que se mueve el Sol en su órbitaalrededor del centro de la galaxia) se encuentra en Hércules, cerca de ξ Herculis.
[editar] Estrellas principales
- α Herculis (Ras Algethi o Rasalgethi), de magnitud 3,31, es un sistema estelar triple, cuya estrella principal es una gigante roja variable.
- β Herculis (Kornephoros), la más brillante de la constelación con magnitud 2,78, una estrella gigante amarilla.
- γ Herculis, gigante blanca de magnitud 3,74. Es una binaria espectroscópica con un período orbital de 11,9 días.
- δ Herculis (Sarin), estrella blanca de magnitud 3,12; es una estrella binaria cuyas componentes han sido resueltas por interferometría.
- ε Herculis, binaria espectroscópica de magnitud 3,91.
- ζ Herculis, la segunda más brillante de la constelación con magnitud 2,89, estrella doble formada por dos estrellas amarillas de desigual brillo.
- η Herculis, gigante amarilla de magnitud 3,49.
- θ Herculis, gigante luminosa naranja de magnitud 3,85.
- ι Herculis, subgigante azul de magnitud 3,79; tres estrellas más completan este sistema estelar cuádruple.
- κ Herculis A y κ Herculis B, dos gigantes que forman una doble óptica.
- λ Herculis (Maasym), gigante naranja de magnitud 4,40.
- μ Herculis, sistema estelar cercano que dista del Sistema Solar 27,4 años luz.
- π Herculis, gigante naranja de magnitud 3,16.
- ρ Herculis, estrella doble cuyas componentes, separadas 4 segundos de arco, brillan con magnitud 4,56 y 5,42.
- τ Herculis, estrella B pulsante lenta (SPB) con una tenue compañera a 7,6 segundos de arco.
- χ Herculis, enana amarilla de baja metalicidad que se encuentra a 52 años luz de distancia.
- ω Herculis (Kajam), de magnitud 4,57.
- 8 Herculis, estrella blanca de magnitud 6,13 que forma una doble óptica con Kappa Herculis —separación 0,2º—.
- 14 Herculis, enana naranja a 59,2 años luz con una enana marrón o planeta gigante alrededor. En 2006 se descubrió un posible segundo compañero, aún sin confirmar.
- 30 Herculis (g Herculis), gigante roja y variable semirregular cuyo brillo oscila entre magnitud 4,3 y 6,3 en un ciclo de 89,2 días.
- 68 Herculis (u Herculis), binaria eclipsante en donde existe transferencia de masa desde la secundaria hacia la primaria.
- 72 Herculis (w Herculis), enana amarilla similar al Sol a 47 años luz de distancia.
- 89 Herculis, supergigante amarilla en las etapas finales de su evolución estelar.
- 95 Herculis, estrella binaria compuesta por una gigante blanca y una gigante amarilla separadas 6,3 segundos de arco.
- 99 Herculis, binaria de baja metalicidad cuya primaria es una enana amarilla de magnitud 5,20.
- 101 Herculis, gigante blanca de magnitud 5,11.
- 109 Herculis, gigante naranja de magnitud 3,84, la duodécima estrella más brillante de la constelación.
- 111 Herculis, estrella blanca de magnitud 4,35.
- X Herculis, variable pulsante semirregular cuyo brillo varía entre magnitud 6 y 7 en un período de 95 días.
- SZ Herculis y FN Herculis, binarias eclipsantes de magnitud 9,94 y 11,08 respectivamente.
- UX Herculis, binaria eclipsante de magnitud 9,05; durante el eclipse principal su brillo disminuye 1,16 magnitudes.
- OP Herculis, gigante luminosa roja variable entre magnitud 5,85 y 6,73.
- HD 147506, subgigante amarilla en donde se ha detectado un planeta masivo (HAT-P-2b) en una órbita excéntricacercana a la estrella.
- HD 149026, estrella subgigante con un planeta cuya masa es similar a la de Saturno.
- HD 154345, enana amarilla a 58,91 años luz con un planeta extrasolar.
- Gliese 623, estrella binaria compuesta por dos enanas rojas.
- Gliese 686 y Gliese 649, enanas rojas a 26,5 y 33,7 años luz respectivamente; la segunda de ellas posee un planeta.
- HD 155358, estrella de baja metalicidad con dos planetas que interactúan gravitacionalmente.
- Gliese 638 y HR 6806, enanas naranjas situadas respectivamente a 31,9 y 36,2 años luz de distancia de la Tierra.
- GD 362, enana blanca con un anillo similar a los de Saturno.
- http://es.wikipedia.org/wiki/H%C3%A9rcules_(constelaci%C3%B3n)
  
ISLA SAN GIORGIO (VENECIA)=GEORGE LEMAITRE
GEMATRIA EN INGLES DE SEED=33
GEMATRIA EN INGLES DE GATE=33
SARA (CE-SAREA DE FILIPO)=PARALELO 33
"¡Oh profundidad de las riquezas de la sabiduría (sophia)
y de la ciencia (gnwsiV, gnosis) de Dios!
¡Cuán incomprensibles son sus juicios, e inescrutables sus caminos!"
(Romanos, 11: 33).
25 DE ABRIL=DIA DE SAN MARCOS
22 DE JULIO=DIA DE MARIA LA MAGDALENA
|
|
|
|
|
|
|
جواب |
رسائل 75 من 83 في الفقرة |
|
|
|
|
جواب |
رسائل 76 من 83 في الفقرة |
|
|

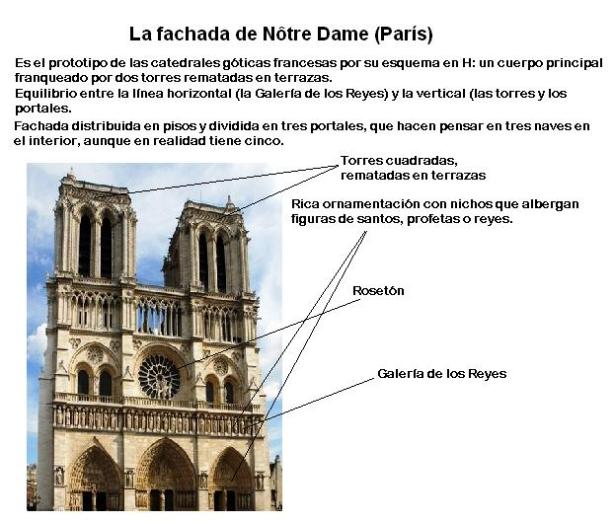
LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
Incendio Notre Dame: Última hora de la catedral de París (15 DE ABRIL)

 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor 
The DaVinci Code, Notre Dame Cathedral from DaVinci Code
original movie prop
 
        

August 23, 2018/

The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
|
جواب |
رسائل 77 من 83 في الفقرة |
|
ES OBVIO EL NEXO DE LA SERPIENTE CON LA MUJER
NOTEN EL NEXO DE DAN, CON LA SERPIENTE (VENECIA) Y EL CABALLO (PLAZA SAN MARCOS)
7. Génesis 49:17 Será Dan SERPIENTE junto al camino, Víbora junto a la senda, Que muerde los talones del caballo, Y hace caer hacia atrás al jinete.
|
|
|
|
جواب |
رسائل 78 من 83 في الفقرة |
|

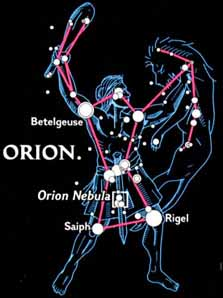
SIRIO ES LA CONSTELACION DEL PERRO/ CAN MAYOR
Nebulosa Cabeza de Caballo
De Wikipedia, la enciclopedia libre
| Nebulosa Cabeza de Caballo |
 |

Statue of Liberty
The height of the Statue of Liberty is 111′-1″ from bottom of foot to top of head. The 7 rays on the crown and the 11 points of the base star echo the proportions of the Great Pyramid’s 7:11 height to base proportion. The superb book Talisman by Graham Hancock and Robert Bauval convincingly shows this goddess is actually the Egyptian Isis.

Image courtesy Elcobbola under the Creative Commons Attribution-Share Alike 3.0 Unported license.
http://www.viewzone.com/onstott66.html


hace 3 días - Manipularon la historia a través de las fuentes de los textos en su lenguaje inventado llamado Latín, peeeeero no pudieron cambiar el ... Jose Alfonso Hernando ... la famosa batalla de Troya, y HASTA AHÍ NOS VAMOS PARA VER QUE ... “Las matemáticas nos hacen más libres y menos manipulables”.
hace 3 días - Principal / Valdeande Magico / ¡¡¡ Visitamos TROYES, donde fue la Guerra de Troya !!! ¡¡¡ Visitamos TROYES, donde fue la Guerra de Troya !!!
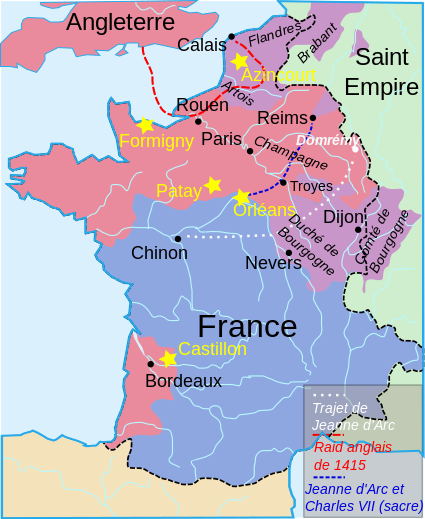

Troyes is the former capital of Champagne and is a perfect short trip visit from Paris. At just an hour and a half by train it can be a day trip but a couple of days and an overnight stay would be better because there’s so much to see and do in this lovely, vibrant city.
A town that is shaped like a Champagne cork in Champagne?
Troyes is an ancient city, once a Roman town with a direct road from Milan and onwards to Boulogne-sur-Mer on the Opal Coast in the north of France – the route for the invasion of Britain. Later the rich and powerful Counts of Champagne built a palace in Troyes and it was a prosperous place that attracted merchants from all over Europe. The counts fortified their town and though at that time Champagne didn’t even exist, the walls took the form of a Champagne cork.
Following a huge fire in 1524 that destroyed many of the ancient buildings that were constructed from wood, new brick buildings were erected and many of them remain to this day. Indeed the inhabitants of Troyes lived in these buildings pretty much as they had been for hundreds of years right up until the 1950s. It was a decade when the town council went on a bit of a renovation rampage to improve conditions since many of the old buildings had no bathrooms and poor hygiene conditions.
Fortunately they didn’t destroy too much and visiting Troyes is like stepping back in time. Every street seems to have its quota of half-timbered houses and there are cobbled streets and tiny alleyways that create a mesmerising maze in the centre of the old town of Troyes. In the little ruelle des Chats (Cats Alley) you’ll see it is so narrow that the houses lean in and touch via a central gutter at the top and cats could cross from houses on both sides of the roads. At the side of the office of the Mutuelle Societe at 111 rue Emile Zola you can enter a gate and at the back you’ll discover a stunning renaissance house looking exactly as it did when it was built. At the Cour du Mortier d’or, the ancient timber frames still bear the workman’s trademarks.
Everywhere you go here you’ll discover traces of history from hundreds of years ago, quaint, quirky and irresistibly charming…
Read the rest of this story in our free magazine – click here to go straight to it!
|
|
|
|
جواب |
رسائل 79 من 83 في الفقرة |
|


https://es.wikipedia.org/wiki/Albert_Einstein
Albert Einstein (en alemán [ˈalbɛɐ̯t ˈaɪnʃtaɪn]; Ulm, Imperio alemán, 14 de marzo de ... En 1915 presentó la teoría de la relatividad general, en la que reformuló por completo el concepto de gravedad. ...... Einstein, Albert (1905e) [manuscrito recibido 27 de septiembre 1905], «Ist die Trägheit eines Körpers von seinem ...
rpp.pe › Lima
27 sep. 2015 - ... primera vez su Teoría de la Relatividad Especial, también llamada restringida; y en 1960, muere el ... 27 de septiembre del 2015 - 12:01 AM ...
ar.tuhistory.com/etiquetas/teoria-de-la-relatividad
Albert Einstein publica la teoría general de la relatividad ... De la teoría especial de la relatividad se deduce su famosa ecuación E=mc2, ... 27-09-1905 D.C..
https://www.gabitos.com/DESENMASCARANDO_LAS_FALSAS.../template.php?...
7 ene. 2014 - En 1905 Einstein publicó su teoría de la relatividad especial, que ...... Einstein presentó a los editores de Annalen el 27 de septiembre del ...
MATT 16:18 is an in your face glyph for the golden mean ratio 1.618
(“MATT” is pun of “MATTER”)
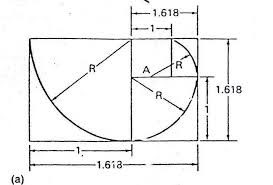
Golden Mean ratio of 1.618

The Golden Mean and the Equilateral Triangle in a Circle; THE CRUCIAL FACT IS THE MIDPOINT OF THE TRIANGLE SIDE
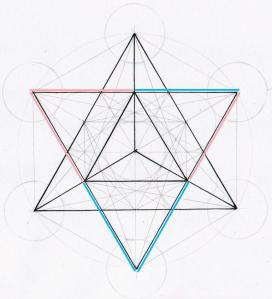
Star Tetrahedron, formed by the MIDPOINTS OF THE CENTRAL EQUILATERAL TRIANGLE (the blue and rose colored lines indicate these midpoint halves)
Saint Mary Magdalene in Venice
 A closer look 
 the Apple
|
|
|
|
جواب |
رسائل 80 من 83 في الفقرة |
|
BENJAMIN/LOBO/PERRO/GUERRA/MARTE/HORUS
EN ESTE VERSICULO ESTA LA CLAVE DE LOS VIAJES EN EL TIEMPO
|
|
|
|
جواب |
رسائل 81 من 83 في الفقرة |
|
ISLA SAN GIORGIO (VENECIA)=GEORGE LEMAITRE
GEMATRIA EN INGLES DE SEED=33
GEMATRIA EN INGLES DE GATE=33
SARA (CE-SAREA DE FILIPO)=PARALELO 33
"¡Oh profundidad de las riquezas de la sabiduría (sophia)
y de la ciencia (gnwsiV, gnosis) de Dios!
¡Cuán incomprensibles son sus juicios, e inescrutables sus caminos!"
(Romanos, 11: 33).
 the Apple
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|

|
|
|
|
جواب |
رسائل 82 من 83 في الفقرة |
|
|
|
|
جواب |
رسائل 83 من 83 في الفقرة |
|
|
|
 أول أول
 سابق
69 a 83 de 83
لاحق سابق
69 a 83 de 83
لاحق
 آخر
آخر

|
|
| |
|
|
©2026 - Gabitos - كل الحقوق محفوظة | |
|
|

