|
|
General: EINSTEIN=LEY DE LA RELATIVIDAD="AGUJERO DE GUSANO"=JUAN MARCOS=TABERNACULOS
Escolher outro painel de mensagens |
|
|
FIESTA DE JUAN MARCOS, EN LA IGLESIA ORTODOXA GRIEGA, EN LIBRA=JUSTICIA=DAN-27 DE SEPTIEMBRE
JUAN MARCOS ESTA ENTERRADO EN VENECIA/VENUS /VIRGEN/ISRAEL-RELACION CON LA TEORIA DE LA RELATIVIDAD DE EINSTEIN (27 DE SEPTIEMBRE DE 1905)
San Marcos
De Enciclopedia Católica
San Cirilo VI llevando las reliquias de San Marcos. Se debe agrandar la imagen para poder ser vista con claridad
(Griego, Markos, latín, Marcus). Se asume en este artículo que el individuo al que se refieren los Hechos como Juan Marcos (12,12.25; 15,37), Juan (13,5.13), Marcos (15,39) es idéntico al Marcos mencionado por San Pablo ( Col. 4,10; 2 Tim. 4,11; Flm. 24) y por San Pedro (1 Ped. 5,13).
Reliquias de Marcos en la Catedral Patriarcal Copta de El Cairo.
Su identidad no es cuestionada por ningún escritor antiguo notable, aunque se sugiere fuertemente, por un lado por el hecho de que el Marcos de las Epístolas Paulinas era el primo ( o anepsios) de Bernabé (Col. 4,10), a quien el Marcos de los Hechos parece haber estado ligado por algún vínculo especial (Hch. 15,37.39); por otro lado, por la probabilidad de que Marcos, a quien San Pedro llama su hijo (1 Ped. 5,13), no es otro que el hijo de María, la vieja amiga de los Apóstoles en Jerusalén (Hch. 12,12).
Sepulcro de San Marcos en Venezia.
]] Al nombre judío de Juan le fue añadido el sobrenombre romano Marco, y por este último fue comúnmente conocido para los lectores de los Hechos (15,37, ton kaloumenon Markon) y de las Epístolas. La madre de Marcos fue un miembro prominente de la incipiente Iglesia en Jerusalén; fue a su casa que Pedro regresó después de ser liberado de la prisión; a la casa se entraba por un porche ( pulon), allí había una niña esclava ( paidiske), probablemente la portera, para abrir la puerta, y la casa era un lugar de reunión para los hermanos, “muchos” de los cuales estaban orando allí la noche que San Pedro llegó de la prisión (Hch. 12,12-13).
Cuando, con ocasión de la hambruna del 45-46 d.C., Bernabé y Saulo habían completado su ministerio en Jerusalén, se llevaron a Marcos con ellos de regreso a Antioquía (Hch. 12,25). No mucho tiempo después, cuando comenzaron el primer viaje apostólico de San Pablo, llevaron a Marcos con ellos como una especie de asistente (hupereten, Hch. 13,5); pero la vaguedad y la variedad de significado del término griego hace incierto saber en qué capacidad precisa actuó. Sin haber sido seleccionado por el Espíritu Santo, ni delegado por la Iglesia de Antioquía, como lo fueron Bernabé y Saúl (Hch. 13,2-4), probablemente Marcos fue tomado por los Apóstoles como alguien que podía ser de ayuda general. El contexto de Hch. 13,5, sugiere que él ayudo incluso en la prédica de la Palabra. Cuando Pablo y Bernabé resolvieron avanzar desde Perge hacia el interior de Asia Menor, Marcos se separó de ellos, si, de hecho, no lo había hecho en Pafos, y regresó a Jerusalén (Hch. 13,13). No podemos decir con certeza cuáles fueron las razones de su regreso; Hechos 15,38, parece sugerir que le temía al trabajo duro. En todo caso, San Pablo no olvidó el incidente, y por esto se rehusó a llevar a Marcos en su segundo viaje apostólico. Esta negativa llevó a la separación de Pablo y Bernabé, y este último se llevó a Marcos en su viaje a Chipre (Hch. 15,37-40). En este punto (49-50 d.C.) perdemos de vista a Marcos en los Hechos, y no volvemos a encontrarlo en el Nuevo Testamento, hasta que aparece cerca de diez años más tarde como compañero de trabajo de san Pablo, y en la compañía de San Pedro en Roma.
San Pablo, al escribir a los colosenses durante su primer encarcelamiento en Roma (59-61 d.C.), dice: “Os saludan Aristarco, mi compañero de cautiverio, y Marcos, primo de Bernabé, acerca del cual recibiste ya instrucciones. Si va a vosotros, dadle buena acogida” (Col. 4,10). Cuando se escribió esto, es evidente que Marcos estaba en Roma, pero tenía cierta intención de visitar Asia Menor. Alrededor de la misma época, San Pablo envía saludos de Marcos a Filemón, a quien menciona entre sus colaboradores (sunergoi, Flm., 24). La intención del evangelista de visitar Asia Menor pudo haberse llevado a cabo, ya que San Pablo, escribiendo a Timoteo en Éfeso poco antes de su muerte le pide que recoja a Marcos y lo traiga con él a Roma, añadiendo: “pues me es muy útil para el ministerio” (2 Tim. 4,11). Si Marcos viajó a Roma en esa época, probablemente estaba allí cuando San Pablo fue martirizado.
Volviendo a la Primera Epístola de Pedro, 5,13, leemos: “Os saluda la que está en Babilonia, elegida como vosotros, así como mi hijo Marcos” (Markos, o uios mou). Esta carta fue dirigida a varias Iglesias de Asia Menor (1 Ped. 1,1) y podemos concluir que ellos conocían a Marcos. Por lo tanto, aunque él rehusó penetrar en Asia Menor con Pablo y Bernabé, San Pablo lo hace probable, y San Pedro lo asegura, que él fue luego, y el hecho de que San Pedro envía saludos de Marcos a un número de Iglesias implica que él debió ser ampliamente conocido allí. Al llamar a Marcos “su hijo”, Pedro podría implicar posiblemente que él lo había bautizado, aunque en ese caso se puede esperar teknon en vez de uios (cf. 1 Cor. 4,17; 1 Tim. 1,2.18; 2 Tim. 1,2; 2,1; Tito 1,4; Flm. 10). No es necesario tomar el término para implicar más que una relación afectiva por un hombre joven, quien tiempo atrás se sentaba a los pies de Pedro en Jerusalén, y cuya madre había sido la amiga de los Apóstoles (Hch. 12,12). En cuanto a la Babilonia desde la que escribe Pedro, y en la cual Marcos está presente con él, no pude caber duda de que se trate de Roma. Todos los primeros Padres que hablan del asunto apoyan la opinión de San Jerónimo: “San Pedro también menciona a este Marcos en su Primera Epístola, cuando se refiere figurativamente a Roma bajo el título de Babilonia” (De vir. Ilustr., 8). Puede decirse que había sido cuestionado por primera vez por Erasmo, a quien siguió un número de escritores protestantes, que ellos podrían haber negado fácilmente la conexión de San Pedro con Roma. De esta manera, encontramos a Marcos en Roma con San Pedro en la época cuando él ya era ampliamente conocido en las Iglesias de Asia Menor. Si suponemos que Marcos viajó a Asia Menor después de la fecha de la Epístola a los Colosenses, que permaneció allí por algún tiempo, y que regresó a Roma antes de que San Pedro escribiese su Primera Epístola, las referencias de San Pablo y de San al evangelista son muy claras y consistentes.
La fecha de la muerte de Marcos es incierta. San Jerónimo ("De Vir. Illustr.", VIII) la asigna el octavo año de Nerón (62-63) (Mortuus est octavo Neronis anno et sepultus Alexandriæ), pero esta es probablemente una conclusión a partir de las afirmaciones de Eusebio ("Hist. eccl.", II.24), de que en ese año Aniano sucedió a San Marcos en la Sede de Alejandría. Ciertamente, si san Marcos estaba vivo cuando se escribió la Segunda Epístola a Timoteo (2 Tm. 4,11), no pudo haber muerto en el año 61 ó 62.; ni Eusebio no dice que Marcos hubiera muerto; el historiador simplemente dice que entonces san Marcos renunció a su sede, y dejó Alejandría para reunirse con Pedro y Pablo en Roma. En cuanto a la manera en que murió, los “Hechos” de Marcos le dan al santo la gloria del martirio, y dicen que murió mientras era arrastrado por las calles de Alejandría; así mismo se cuenta en la Crónica Pascual. Pero no tenemos evidencia anterior al siglo IV de que el santo fue martirizado. Este silencio temprano, sin embargo, no es del todo decisivo contra la verdad de las tradiciones posteriores. Para la supuesta conexión del santo con Aquilea, ver “Acta SS”, XI, págs. 346-7. y acerca del traslado de su cuerpo de Alejandría a Venecia y su veneración allí, ibid, págs. 352-358. E n la literatura y el arte cristianos San Marcos es representado simbólicamente por un león. Las Iglesias Latina y Griega celebran su fiesta el 25 de abril, pero la Iglesia Griega guarda también la fiesta de Juan Marcos el 27 de septiembre.
Fuente: MacRory, Joseph. "St. Mark." The Catholic Encyclopedia. Vol. 9. New York: Robert Appleton Company, 1910. <http://www.newadvent.org/cathen/09672c.htm>.
neetescuela.com/tag/teoria-de-la-relatividad-de-einstein/
Cristina | 27 septiembre, 2011 | 1 Comentario. La teoría de la relatividad fue
formulada por el fisico aleman Albert Einstein (1879-1955), quien publicó en
1905 ...
centros5.pntic.mec.es/ies.victoria.kent/Rincon-C/.../1905.html
En este artículo, Einstein introduce la teoría de la relatividad. 27 de septiembre -
Ist die Traghëit eines Körpes von seinem Energieinhalt abhängig? (¿Depende ...
www.fte-energia.org/E60/e60-16.html
2005, 100 años de la Teoría de la Relatividad Especial .... Este artículo fue
recibido por la revista alemana de física el 27 de septiembre de 1905 y fue
publicado ...
www.zamandayolculuk.com/cetinbal/.../TeoriaDeLArelatividad.htm
El 27 de Septiembre de 1905, Einstein añade como una posdata al artículo de la
Relatividad Restringida un corto trabajo de tres páginas en el que estable una ...
[PDF]
fundacionorotava.org/.../SCC%20epoca%20de%20Einstein/.../BIOGRAFIA1. pdf
1879 El 14 de marzo, a las 11:30. nace Albert Einstein, en la ciudad alemana de
Ulm. ... 27 de septiembre llega, a losAmialcn der Physik, el segundo artículo
sobre la relatividad especial en el que Einstein expone por primera vez su
famosa.
www.muyinteresante.es/.../el-siglo-de-la-relatividad-el-gran-legado-de- einstein
2 Feb 2005 ... Lo más sorprendente es lo que Einstein mostró a los editores de Annalen el 27
de septiembre: masa y energía son intercambiables y están ...
es.wikipedia.org/wiki/Equivalencia_entre_masa_y_energía
... entre la masa y la energía dada por la expresión de la teoría de la relatividad
de Einstein. E = mc^2 .... publicado en Annalen der Physik el 27 de septiembre).
|
|
|
|
|
FIESTA DE JUAN MARCOS, EN LA IGLESIA ORTODOXA GRIEGA, EN LIBRA=JUSTICIA=DAN-27 DE SEPTIEMBRE
San Marcos
De Enciclopedia Católica
San Cirilo VI llevando las reliquias de San Marcos. Se debe agrandar la imagen para poder ser vista con claridad
(Griego, Markos, latín, Marcus). Se asume en este artículo que el individuo al que se refieren los Hechos como Juan Marcos (12,12.25; 15,37), Juan (13,5.13), Marcos (15,39) es idéntico al Marcos mencionado por San Pablo ( Col. 4,10; 2 Tim. 4,11; Flm. 24) y por San Pedro (1 Ped. 5,13).
Reliquias de Marcos en la Catedral Patriarcal Copta de El Cairo.
Su identidad no es cuestionada por ningún escritor antiguo notable, aunque se sugiere fuertemente, por un lado por el hecho de que el Marcos de las Epístolas Paulinas era el primo ( o anepsios) de Bernabé (Col. 4,10), a quien el Marcos de los Hechos parece haber estado ligado por algún vínculo especial (Hch. 15,37.39); por otro lado, por la probabilidad de que Marcos, a quien San Pedro llama su hijo (1 Ped. 5,13), no es otro que el hijo de María, la vieja amiga de los Apóstoles en Jerusalén (Hch. 12,12).
Sepulcro de San Marcos en Venezia.
]] Al nombre judío de Juan le fue añadido el sobrenombre romano Marco, y por este último fue comúnmente conocido para los lectores de los Hechos (15,37, ton kaloumenon Markon) y de las Epístolas. La madre de Marcos fue un miembro prominente de la incipiente Iglesia en Jerusalén; fue a su casa que Pedro regresó después de ser liberado de la prisión; a la casa se entraba por un porche ( pulon), allí había una niña esclava ( paidiske), probablemente la portera, para abrir la puerta, y la casa era un lugar de reunión para los hermanos, “muchos” de los cuales estaban orando allí la noche que San Pedro llegó de la prisión (Hch. 12,12-13).
Cuando, con ocasión de la hambruna del 45-46 d.C., Bernabé y Saulo habían completado su ministerio en Jerusalén, se llevaron a Marcos con ellos de regreso a Antioquía (Hch. 12,25). No mucho tiempo después, cuando comenzaron el primer viaje apostólico de San Pablo, llevaron a Marcos con ellos como una especie de asistente (hupereten, Hch. 13,5); pero la vaguedad y la variedad de significado del término griego hace incierto saber en qué capacidad precisa actuó. Sin haber sido seleccionado por el Espíritu Santo, ni delegado por la Iglesia de Antioquía, como lo fueron Bernabé y Saúl (Hch. 13,2-4), probablemente Marcos fue tomado por los Apóstoles como alguien que podía ser de ayuda general. El contexto de Hch. 13,5, sugiere que él ayudo incluso en la prédica de la Palabra. Cuando Pablo y Bernabé resolvieron avanzar desde Perge hacia el interior de Asia Menor, Marcos se separó de ellos, si, de hecho, no lo había hecho en Pafos, y regresó a Jerusalén (Hch. 13,13). No podemos decir con certeza cuáles fueron las razones de su regreso; Hechos 15,38, parece sugerir que le temía al trabajo duro. En todo caso, San Pablo no olvidó el incidente, y por esto se rehusó a llevar a Marcos en su segundo viaje apostólico. Esta negativa llevó a la separación de Pablo y Bernabé, y este último se llevó a Marcos en su viaje a Chipre (Hch. 15,37-40). En este punto (49-50 d.C.) perdemos de vista a Marcos en los Hechos, y no volvemos a encontrarlo en el Nuevo Testamento, hasta que aparece cerca de diez años más tarde como compañero de trabajo de san Pablo, y en la compañía de San Pedro en Roma.
San Pablo, al escribir a los colosenses durante su primer encarcelamiento en Roma (59-61 d.C.), dice: “Os saludan Aristarco, mi compañero de cautiverio, y Marcos, primo de Bernabé, acerca del cual recibiste ya instrucciones. Si va a vosotros, dadle buena acogida” (Col. 4,10). Cuando se escribió esto, es evidente que Marcos estaba en Roma, pero tenía cierta intención de visitar Asia Menor. Alrededor de la misma época, San Pablo envía saludos de Marcos a Filemón, a quien menciona entre sus colaboradores (sunergoi, Flm., 24). La intención del evangelista de visitar Asia Menor pudo haberse llevado a cabo, ya que San Pablo, escribiendo a Timoteo en Éfeso poco antes de su muerte le pide que recoja a Marcos y lo traiga con él a Roma, añadiendo: “pues me es muy útil para el ministerio” (2 Tim. 4,11). Si Marcos viajó a Roma en esa época, probablemente estaba allí cuando San Pablo fue martirizado.
Volviendo a la Primera Epístola de Pedro, 5,13, leemos: “Os saluda la que está en Babilonia, elegida como vosotros, así como mi hijo Marcos” (Markos, o uios mou). Esta carta fue dirigida a varias Iglesias de Asia Menor (1 Ped. 1,1) y podemos concluir que ellos conocían a Marcos. Por lo tanto, aunque él rehusó penetrar en Asia Menor con Pablo y Bernabé, San Pablo lo hace probable, y San Pedro lo asegura, que él fue luego, y el hecho de que San Pedro envía saludos de Marcos a un número de Iglesias implica que él debió ser ampliamente conocido allí. Al llamar a Marcos “su hijo”, Pedro podría implicar posiblemente que él lo había bautizado, aunque en ese caso se puede esperar teknon en vez de uios (cf. 1 Cor. 4,17; 1 Tim. 1,2.18; 2 Tim. 1,2; 2,1; Tito 1,4; Flm. 10). No es necesario tomar el término para implicar más que una relación afectiva por un hombre joven, quien tiempo atrás se sentaba a los pies de Pedro en Jerusalén, y cuya madre había sido la amiga de los Apóstoles (Hch. 12,12). En cuanto a la Babilonia desde la que escribe Pedro, y en la cual Marcos está presente con él, no pude caber duda de que se trate de Roma. Todos los primeros Padres que hablan del asunto apoyan la opinión de San Jerónimo: “San Pedro también menciona a este Marcos en su Primera Epístola, cuando se refiere figurativamente a Roma bajo el título de Babilonia” (De vir. Ilustr., 8). Puede decirse que había sido cuestionado por primera vez por Erasmo, a quien siguió un número de escritores protestantes, que ellos podrían haber negado fácilmente la conexión de San Pedro con Roma. De esta manera, encontramos a Marcos en Roma con San Pedro en la época cuando él ya era ampliamente conocido en las Iglesias de Asia Menor. Si suponemos que Marcos viajó a Asia Menor después de la fecha de la Epístola a los Colosenses, que permaneció allí por algún tiempo, y que regresó a Roma antes de que San Pedro escribiese su Primera Epístola, las referencias de San Pablo y de San al evangelista son muy claras y consistentes.
La fecha de la muerte de Marcos es incierta. San Jerónimo ("De Vir. Illustr.", VIII) la asigna el octavo año de Nerón (62-63) (Mortuus est octavo Neronis anno et sepultus Alexandriæ), pero esta es probablemente una conclusión a partir de las afirmaciones de Eusebio ("Hist. eccl.", II.24), de que en ese año Aniano sucedió a San Marcos en la Sede de Alejandría. Ciertamente, si san Marcos estaba vivo cuando se escribió la Segunda Epístola a Timoteo (2 Tm. 4,11), no pudo haber muerto en el año 61 ó 62.; ni Eusebio no dice que Marcos hubiera muerto; el historiador simplemente dice que entonces san Marcos renunció a su sede, y dejó Alejandría para reunirse con Pedro y Pablo en Roma. En cuanto a la manera en que murió, los “Hechos” de Marcos le dan al santo la gloria del martirio, y dicen que murió mientras era arrastrado por las calles de Alejandría; así mismo se cuenta en la Crónica Pascual. Pero no tenemos evidencia anterior al siglo IV de que el santo fue martirizado. Este silencio temprano, sin embargo, no es del todo decisivo contra la verdad de las tradiciones posteriores. Para la supuesta conexión del santo con Aquilea, ver “Acta SS”, XI, págs. 346-7. y acerca del traslado de su cuerpo de Alejandría a Venecia y su veneración allí, ibid, págs. 352-358. E n la literatura y el arte cristianos San Marcos es representado simbólicamente por un león. Las Iglesias Latina y Griega celebran su fiesta el 25 de abril, pero la Iglesia Griega guarda también la fiesta de Juan Marcos el 27 de septiembre.
|
 First Previous 2 to 2 of 2 Next  Last |
| Reply |
Message 2 of 2 on the subject |
|
|
|
|
|
|
|
|
|
| Reply |
Message 23 of 25 on the subject |
|
|
|
| Reply |
Message 24 of 25 on the subject |
|
|
|
| Reply |
Message 25 of 25 on the subject |
|
|
| Reply |
Message 81 of 81 on the subject |
|
|
|
|
|
|
|
|
|
|
-
Anunciowww.philadelphiapass.com/
Ahorra Con PhillyPass: Descuentos y Pruébelo y ahorrar en Philadelphia
-
Anunciowww.donorionear.org.ar/Papa-Francisco
¡Conocé la Obra de Don Orione!
-
-
www.familiam.org/.../00009496_El_Papa_Francisco_en_Filadelfia.html
Ya es oficial: el Papa Francisco estará en Filadelfia en septiembre del 2015 para
participar al octavo Encuentro mundial de las familias. Lo anunció él mismo ...
-
www.lanacion.com.ar/1830114-washington-nueva-york-y-filadelfia-dia-por- dia-la-agenda-del-papa-francisco-en-eeuu
Hace 1 minuto. ... Washington, Nueva York y Filadelfia: día por día, la agenda del papa Francisco
en EE.UU. | El pontífice estará seis días en el país, en los que ...
-
https://www.aciprensa.com/noticias/.../encuentro-mundial-de-familias/
El Arzobispo Charles Chaput, inauguró el Encuentro Mundial de las Familias
Filadelfia 2015 al que asistirá el Papa Francisco los días 26 y 27 de septiembre.
-
https://www.facebook.com/WMF2015ES
Homilía del Papa Francisco en la Misa de Canonización de Fray Junípero Serra -
Santuario Nacional de la Inmaculada Concepción, Washington D.C. 23 de ...
-
www.holaciudad.com/el-papa-podria-visitar-filadelfia-el-2015-n399411
El Papa Francisco podría visitar Filadelfia en septiembre del 2015 con motivo del
VIII Encuentro Mundial de las Familias.
|
|
|
|
|
EL PAPA FRANCISCO, EN FILADELFIA, EN EL MISMO DIA QUE EINSTEIN SACO LA "LEY DE LA RELATIVIDAD DEL TIEMPO"
-
Anunciowww.philadelphiapass.com/
Ahorra Con PhillyPass: Descuentos y Pruébelo y ahorrar en Philadelphia
-
Anunciowww.donorionear.org.ar/Papa-Francisco
¡Conocé la Obra de Don Orione!
-
-
www.familiam.org/.../00009496_El_Papa_Francisco_en_Filadelfia.html
Ya es oficial: el Papa Francisco estará en Filadelfia en septiembre del 2015 para
participar al octavo Encuentro mundial de las familias. Lo anunció él mismo ...
-
www.lanacion.com.ar/1830114-washington-nueva-york-y-filadelfia-dia-por- dia-la-agenda-del-papa-francisco-en-eeuu
Hace 1 minuto. ... Washington, Nueva York y Filadelfia: día por día, la agenda del papa Francisco
en EE.UU. | El pontífice estará seis días en el país, en los que ...
-
https://www.aciprensa.com/noticias/.../encuentro-mundial-de-familias/
El Arzobispo Charles Chaput, inauguró el Encuentro Mundial de las Familias
Filadelfia 2015 al que asistirá el Papa Francisco los días 26 y 27 de septiembre.
-
https://www.facebook.com/WMF2015ES
Homilía del Papa Francisco en la Misa de Canonización de Fray Junípero Serra -
Santuario Nacional de la Inmaculada Concepción, Washington D.C. 23 de ...
-
www.holaciudad.com/el-papa-podria-visitar-filadelfia-el-2015-n399411
El Papa Francisco podría visitar Filadelfia en septiembre del 2015 con motivo del
VIII Encuentro Mundial de las Familias.
| Reply |
Message 10 of 10 on the subject |
|
|
| Reply |
Message 10 of 15 on the subject |
|
|
|
|
| Reply |
Message 11 of 15 on the subject |
|
|
|
|
| Reply |
Message 12 of 15 on the subject |
|
|
|
|
| Reply |
Message 13 of 15 on the subject |
|
|
|
|
| Reply |
Message 14 of 15 on the subject |
|
|
|
|
| Reply |
Message 15 of 15 on the subject |
|
|
|
|
|
|
|
|
|
|
|
|
EL PAPA EN FILADELFIA, EN EL MISMO DIA QUE EINSTEIN (27 DE SEPTIEMBRE DE 1905) SACO LA LEY DE LA RELATIVIDAD.
26 Y 27 DE SEPTIEMBRE DE 2015, EN FILADELFIA.
|
|
|
|
|
EINSTEIN / STONE / PIEDRA / MATEO 16:18
|
|
|
|
|
 Jan I did not want to overwhelm the readers on this forum. I have a feeling that folk's eyes glaze over if the posts are too long.  Now in reference to the above imagery and sacred geometry taken from your website Jan, I too have noticed the same 'patterns' being used since time immemorial. And these archetypal connections I feel have something to do with the evolution of our own DNA. As these two blogs reveal...the reason for the architecture of places like St. Peter's Square ellipse.http://kachina2012.wordpress.com/2009/0 ... o-message/http://kachina2012.wordpress.com/2009/0 ... ooks-like/ 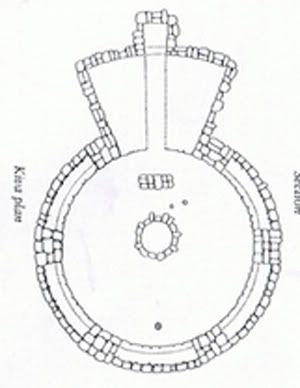 Two images that are upside down images of each other? Tesla Tower on the left, and the ceremonial KIVA AD 500 on the right.  And I found the above symbol in an ole' Templar Church in Garway, England. Along side in the same church we find the Templar Cross, the Right Hand of God (tribe of Ben Yamin), the SWASTIKA and an universal idea, a shape/form found ALL over the world, an inspiration of archetypal universal thought ...  temples that resemble the shape defined by the light bulb? 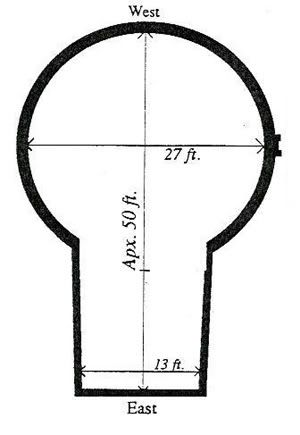 Have I found the same 'treasure' the Templars found? http://kachina2012.wordpress.com/2009/0 ... the-tarot/Was the treasure that the Templars found re: Solomon's Temple, similar to another mathematical gem that a fella called Fibonacci revealed? A numerical code that can be taught to a child?
Quote:
* The spreading of the Hindu-Arabic numeral system in Europe, primarily through the publication in the early 13th century of his Book of Calculation, the Liber Abaci.
* A number sequence named after him known as the Fibonacci numbers, which he did not discover but used as an example in the Liber Abaci.[3]
So who is the original 'discoverer' of this CODE? Did the Egyptians use it 1000s of years before Fibonacci resurrected it? There is a dispute as to whether the Egyptians were aware of this CODE that mimics nature. I have proof they were aware of it long before the Greek mathematicians who are credited with many FIBs. I believe what the Knights Templar found was something quite simple, a universal irrational complexity reduced to a simplicity.Revealed by a simple logarithmic pattern found all throughout NATURE, named after Fibonacci. Of course the irrational irony of the poetic universe suggests that this CODE is being used to veil some very very very big FIBs, including something called the Big BANG.  Fibonacci = 112358 = phi = everything GOLDEN ... including the GOLDEN RULES  we must live by? http://kachina2012.wordpress.com/2009/0 ... acci-code/And of course a discussion of the Knights Templar would not be complete without discussing Freemasonry which can be traced to Phreemasonry? The truncated pyramid is found where? 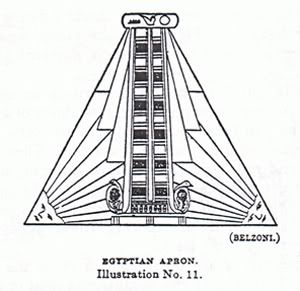  Again sometimes we must flip folks worlds upside down...in order to get them to understand and SEE. Sometimes it becomes necessary within the PRECESSION cycle to FLIP the world over on its x-axis?    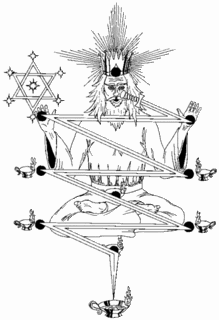Of course the simplest representation of ALL the above shapes could simply be the shape of a magnet or a U or a YOU or a EWE? With an invisible 3rd pole placed between the other two? Just like the Tree of Life which has 3 distinct pillars?Free Will suggests you can be a U or a EWE? Free Will suggests you can be part of the structure representing the tree/magnet OR simply the iron filings that get 'directed' by the 'field' created? That is your choice. To be part of the U-niversal Magnet or simply a follower, an iron filing, a sheeple, directed where to go...? namaste
EINSTEIN (STEIN=PIEDRA EN ALEMAN)= STONE= MATEO 16:18 |
|
|
|
|
vision-master wrote:
I just spilled my coffee.  Is your cup half full or half empty now? I just had a thought...followed by the truth chill...which means I am getting warmer. Let me present what I believe to be...3 representations of the SUN bending the fabric of SpaceTime.   1st image on the left has the SUN represented by the 6 pointed Star of David/hexagram/hexagon in the center of the Freemason Tracing Board. And it is no coincidence that the 6x6 magic square is also associated with the SUN. 2nd image in the center is Einstein's explanation. 3rd image is my addendum to ALL of the above...the "what goes up, must come down" theory of gravity... (what kind of rotations/flips/tricks can ganesh do...well it all depends on the escape velocity, the height attained?) Apparently EINSTEIN forgot to apply the fundamental action/reaction law. For every action there is a reaction... That Elephant or Sun bending SPACETIME fabric could be the result of a pulsation similar to how a speaker pulsates..or or or the magic we see in CYMATICS. What if the membrane covering the black hole called the event horizon is similar to a trampoline? And the mass of sun bends SPACETIME in a similar manner to a trampoline? And what if we should prepare for what Einstein forgot to incorporate into his theory. REACTION force... Spring is coiled? What if? Just a needed addendum to the theory of relativity...and other blah blah blah. SO GRAVITY is somehow connected to SOUND waves? namaste
_________________
KEY 528=Swastika=ancient Spherical Standing Wave Theory
“A theory is more impressive the greater is the simplicity of its premise, the more different are the kinds of things it relates and the more extended its range of applicability…”
-Einstein http://2012forum.com/forum/viewtopic.php?p=213550 |
|
|
|
|
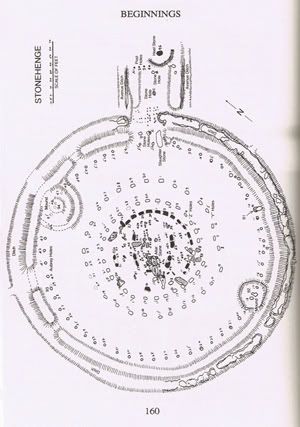 re: Stonehengeimportant to note that there are 56 Aubrey holes NOT 55 as I have found in other *temples* I do wonder why? Leave it with me. I will help figure it out. Help take all of this mumbo jumbo gumbo zoup to the next level of understanding. >>> http://kachina2012.wordpress.com/2008/0 ... d-temples/because as I have already illustrated on this thread and elsewhere, that Stonehenge *fits* into the KEYHOLE/LIGHT-BULB form that is shared with many other sacred temples found in other *unrelated* CULTures. how can that be? why do we find these KEYHOLES / Light Bulbs everywhere? Hey I have an idea and guess what? IDEAS are MEMES.What we know is that these *temples* were in some way associated with a healing process involving our DNA. The architecture implies that by entering the temple we are going within...right down to the atomic level. WHY does it imply there is tinkering at the atomic level of our DNA by entering these temples?
WHAT is the clue that tipped me off?
It is implied because it is at the atomic level NOT at the molecular level, where we encounter the number/concept of 55.
55 atoms that comprise the base pairs = 55 black and white dots that comprise the I Ching architecture.At the molecular level we encounter the number concept of 64 that connects the 64 DNA codons to the 64 hexagrams used in the I Ching. And in making a comparison of St. Peter's Square to Stonehenge and ALTARS used, the stone called the Heel Stone is coincidently about the same distance from the center, that we see in St. Peter's square, i.e. the distance from the obelisk to the black door, where they bury the Popes is in a similar proportion. So why else would you call it the Heal Stone err I meant to say the Heel Stone? I believe it is time to investigate these sites and others for clues as to why 56 Aubrey Holes were employed and not 55 like we found in the Great Pyramid, in Mecca, in the I Ching and in the our own DNA. http://sarsen56.wordpress.com/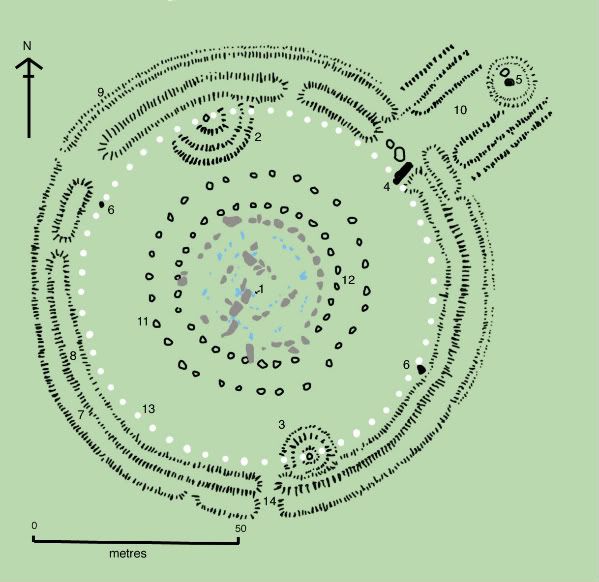 Key to plan:1 = The Altar Stone, a six ton monolith of green micaceous sandstone from Wales 2 = barrow without a burial 3 = "barrows" (without burials) 4 = the fallen Slaughter Stone, 4.9 metres long 5 = the Heel Stone 6 = two of originally four Station Stones 7 = ditch 8 = inner bank 9 = outer bank 10 = The Avenue, a parallel pair of ditches and banks leading 3 km to the River Avon 11 = ring of 30 pits called the Y Holes 12 = ring of 29 pits called the Z Holes 13 = circle of 56 pits, known as the Aubrey holes 14 = smaller southern entrance The site as of AD 2004. The plan omits the trilithon lintels for clarity. Holes that no longer, or never, contained stones are shown as open circles and stones visible today are shown coloured, grey for sarsen and blue for the imported stone, mainly bluestone. http://en.wikipedia.org/wiki/File:Stonehenge_plan.jpgSo does anybody have any IDEAS or MEMES they want to spread around tOWN? Something they rEMEMbEr but can not quite make out...? namaste SS/55
_________________
KEY 528=Swastika=ancient Spherical Standing Wave Theory
“A theory is more impressive the greater is the simplicity of its premise, the more different are the kinds of things it relates and the more extended its range of applicability…”
-Einstein http://2012forum.com/forum/viewtopic.php?p=365163 |
|
|
|
|
10 Commandments all summed up.... The sum of 10 is 551 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55The 10th number in the Fibonacci series is 551, 1, 2, 3, 5, 8, 13, 21, 34, 5555 appears as a boundary marker of sorts. i.e. >>> The mesosphere (above the stratosphere) extends from 30 miles (48 kilometers) to 55 miles (85 kilometers) above the earth. Temperatures decrease with altitude to 130F (90C). >>> The ionosphere is a region of the atmosphere that overlaps the others, reaching from 30 miles (48 kilometers) to 250 miles (402 kilometers). In this region, the air becomes ionized (electrified) from the suns ultraviolet rays, etc. This area affects the transmission and reflection of radio waves. It is divided into three regions: the D region (at 35 to 55 miles, or 56 to 88 kilometers), the E Region (Heaviside-Kennelly Layer, 55 to 95 miles, or 56 to 153 kilometers), and the F Region (Appleton Layer, at 95 to 250 miles, or 153 to 402 kilometers). >>> The estimated distance to the ‘edge’ of our solar system is about 55 au. (1 au = 93 million miles)
Quote:
Study: Upper layer of atmosphere shrinking(Agencies) Updated: 2010-08-27 10:29 According to the study, published in the American Geophysical Union's journal Geophysical Research Letters, the sun's energy output was unusually low from 2007 to 2009. During that period the atmospheric layer called the thermosphere - from 55 miles to 300 miles (90 to 480k) above the Earth - cooled and shrank.>>> http://www.chinadaily.com.cn/world/2010 ... 213148.htmAll coincidences I assure you, if you want to believe in coincidences. But there are none. It is design appearing on every level. Below is an image of the first two of those frescos. I find it interesting that the combined image appears as though we are looking through binoculars. There were 27 pairs of binocular stereo-vision frescos. With the last ONE placed above a doorway. At the time I did not understand the importance of the LINTEL. But the Freemasons are one group of many that place great importance in the LINTEL that spans the two pillars, which the Freemasons and Kabbalists refer to as Jachin and Boaz. The reason for two pillars inside a temple is the same reason we find many gothic churches have two steeples instead of one. However the Christian church with the tallest steeple in the world at 528 feet, is located in the hometown of Albert Einstein, in Ulm Germany.
Quote:
It is the tallest church in the world,[1] and the tallest structure built before the 20th century, with a steeple measuring 160.9 metres (528 ft)[1] and containing 768 steps. From the top level at 143 metres (469 ft) there is a panoramic view of Ulm in Baden-Württemberg and Neu-Ulm in Bavaria and, in clear weather, a vista of the Alps from Säntis to the Zugspitze. The final stairwell to the top (known as the third Gallery) is a tall, spiraling staircase that has barely enough room for one person. In 1377 the foundation stone was laid. The planned church was to have three naves of equal height, a main spire on the west and two steeples above the choir. In 1392 Ulrich Ensingen (associated with Strasbourg Cathedral) was appointed master builder. It was his plan to make the western church tower the tallest spire, which it remains in the present day. >>> http://en.wikipedia.org/wiki/Ulm_Minster >>> http://books.google.com/books?id=DtS2iD ... le&f=false Now take a closer look at fresco 1. , way up yonder… I spy with my little eye...   http://kachina2012.wordpress.com/2007/1 ... s-a-whore/ #54 and #55 stereo centers re: organic chemistry??? #56 which was the archway over a door connecting #55 back to #1 .... and I cannot remember for sure if this courtyard, this particular 'archway' leads into the room where I photographed this image below.But I know they are close to each other in proximity, because they are in sequence on my CD file.  namaste XX In the year 1377 the foundation stone was laid for the tallest spire in the world at 528 feet?
In the year 1307 A.D. the Knights Templar reign started to unravel too.And 137 and 528 are numbers associated with Albert Einstein and ME. shhh do not tell anyone I found a sacred KEY in the tarot with the numbers 137 and 528 clearly on it....linked by the number 11? 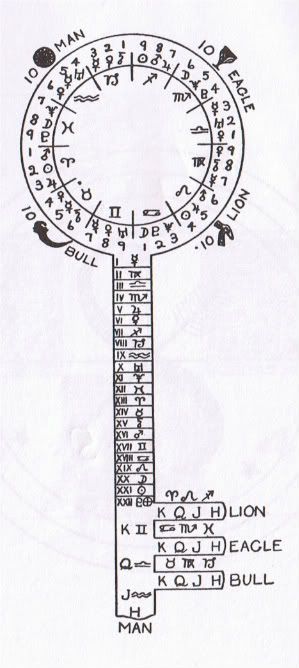 137 and 528 on the same esoteric KEY??? WOW MOM >>> http://kachina2012.wordpress.com/2010/1 ... o-so-much/Where ME is the equivalent of M = E or m = E On what side of the mE equation do I put the c^2?
_________________
KEY 528=Swastika=ancient Spherical Standing Wave Theory
“A theory is more impressive the greater is the simplicity of its premise, the more different are the kinds of things it relates and the more extended its range of applicability…”
-Einstein
http://2012forum.com/forum/viewtopic.php?f=15&t=13121&start=165
|
|
|
|
|
es.walyou.com
2 Alcancia cubo Rubik
521 × 423 - 24k - jpg |
es.wikipedia.org
El interior de un cubo de
232 × 199 - 28k - jpg |
solostocks.com
Cubo Mágico
500 × 500 - 29k - jpg |
pocoseso.com
del Rubik - Cubo Magico -
450 × 338 - 28k - jpg |
Búsquedas relacionadas con cubo magico
EL MISMO "CUBO MAGICO" ES UN HIPERCUBO (HAY UN CUBO MAS CHICO EN EL CENTRO DEL MISMO)
| Reply |
Message 24 of 24 on the subject |
|
El término cuarta dimensión aparece en diversos contextos como la física, las matemáticas y la ciencia ficción. En cada contexto el significado es diferente:
En física, se hace referencia a la cuarta dimensión al hablar del tiempo, principalmente desde el planteamiento de la Teoría de la Relatividad.
En matemática, el concepto aparece asociado o bien a espacios euclídeos de más de tres dimensiones o, más generalmente, a espacios localmente euclídeos o 4-variedades diferenciables.
Hipercubo de 4 dimensiones espaciales girando, tal como se vería proyectado en el espacio tridimensional.
El interés en las dimensiones más altas alcanzó su clímax entre 1870 y 1920.1 En esos años se convirtió en tema frecuente en la literatura fantástica, el arte e incluso algunas teorías científicas. La cuarta dimensión, entendida como dimensión espacial adicional (no como dimensión temporal, como en la teoría de la relatividad) apareció en las obras literarias de Oscar Wilde, Fiódor Dostoyevski, Marcel Proust, H. G. Wells y Joseph Conrad, inspiró algunas obras musicales de Alexander Scriabin, Edgar Varèse y George Antheil y algunas obras plásticas de Pablo Picasso y Marcel Duchamp influyendo en el desarrollo del cubismo. Incluso personajes tan diversos como el psicólogo William James, la escritora Gertrude Stein o el socialista revolucionario Vladimir Lenin se interesaron en el tema.
Igualmente los matemáticos habían estado interesados en el tema al tratar de generalizar los conceptos de la geometría euclídea tridimensional. El matemático Charles L. Dodgson, que enseñó en la Universidad de Oxford, deleitó a generaciones de escolares escribiendo libros, bajo el pseudónimo de Lewis Carroll, que incorporaban algunas ideas sobre la cuarta dimensión. Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann. Charles Howard Hinton, matemático y escritor de ciencia ficción británico, acuñó muchos neologismos para describir elementos en la cuarta dimensión. De acuerdo con el Oxford English Dictionary, fue el primero en emplear la palabra tesseract en su libro Una nueva era del pensamiento. También inventó las palabras “kata” (del griego “abajo”) y “ana” (del griego “arriba”) para describir las dos direcciones opuestas en la cuarta dimensión, equivalentes a derecha-izquierda, arriba-abajo, y adelante-atrás.
Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como "rotaciones" en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la "cuarta dimensión" no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.
Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un "espacio" de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.
Un ángulo recto se describe como un cuarto de una revolución. La Geometría Cartesiana escoge direcciones ortogonales arbitrariamente a través del espacio, lo que significa que cada dirección está en ángulo recto con las demás. Las 3 dimensiones ortogonales del espacio se conocen como altitud, longitud y latitud. La Cuarta Dimensión por lo tanto es la dirección en el espacio con ángulo recto a las 3 direcciones observables.
Un vector espacial es un conjunto de vectores, los cuales podemos imaginarlos como flechas, que proviene de un simple lugar llamado origen (vectores geométricos), que apuntan a otros lugares.
Un punto es un objeto de cero dimensiones. No tiene extensión en el espacio ni propiedades, como una flecha pero sin longitud. Este vector es llamado el vector cero y es el más simple vector espacial.
Una línea es un objeto unidimensional. Si escogemos un cierto vector distinto a cero en una cierta dirección, este vector tiene cierta longitud definida. Ese vector tiene una cabeza en un cierto punto en espacio y una cola en el origen. Si pensamos en estirar que ese vector así sea dos veces su largo, tres veces, etcétera y uniformemente, tomando todas las longitudes posibles (incluso la longitud cero, conseguir el vector cero), conseguiremos una sola línea con una sola dimensión: La de la longitud. Todos los vectores que describen puntos en esta línea serían paralelos. Aunque para visualizar la línea es necesario que ésta tenga un ancho mínimo, sin embargo, una línea de 1D no la tendría.
Un plano es un objeto de dos dimensiones. Tiene longitud y anchura pero no profundidad - algo como una hoja de papel, o más exactamente algo como las imágenes en un televisor común. El pensamiento en un plano en términos de vectores puede ser un poco más desafiante. Si pensamos en tomar un vector y lo movemos de modo que su cola esté tocando la cabeza del primero y esté formando un vector con su cola en el origen y la cabeza en la cabeza del segundo vector colocado de nuevo, tenemos una manera razonable de hablar de vectores de adición. Si tenemos dos vectores que no sean paralelos, podemos hablar de todos los puntos que podemos alcanzar por o solamente el estirar o ningunos de los vectores, y, agregando estos vectores juntos, estos puntos forman un plano.
El espacio, como lo percibimos, es tridimensional. Podemos pensar en poner una línea junto con un plano. Estas líneas son como un emparedado. Para conseguir a un cierto punto en espacio, podemos imaginarnos el viajar encima de la línea y después el movernos a través del plano al punto. Entonces tenemos tres vectores a pensar alrededor, uno a viajar una cierta distancia encima de la línea y dos para conseguir a un cierto punto en espacio.
Para tres rectas ortogonales en el espacio tridimensional (x, y y z) existe una cuarta, normal al espacio, ortogonal a estas tres rectas, que forma un eje p. ej. w.
El producto vectorial es la determinante de una matriz 4×4, donde una de las filas (o columnas) son los vectores unitarios h, i, j y k y las demás (filas o columnas respectivamente) están formadas por las componentes de tres vectores cuadradimensionales cualesquiera, este producto nos dará un cuarto vector perpendicular a estos tres mismos.
La Geometría euclidiana prevé una mayor variedad de formas para existir que en tres dimensiones. Los poliedros tridimensionales son recintos espaciales hechos de caras de dos dimensiones conectadas, los policronos cuadridimensionales son recintos del espacio cuadridimensional hechos de poliedros tridimensionales. Donde en tres dimensiones, hay exactamente cinco poliedros regulares, o los sólidos platónicos, que pueden existir, seis policronos regulares existen en la cuarta dimensión. Cinco de los seis se pueden interpretar como extensiones naturales de los sólidos platónicos, así como el cubo, un sólido platónico, es una extensión del cuadrado de dos dimensiones. El pentachoron está hecho de 5 tetraedros para las caras y 10 caras triangulares, y es el análogo cuadridimensional del tetraedro. El teseracto, o el hipercubo, se compone de 8 caras cúbicas y de 24 cuadrados, y es el politopo cuadridimensional medido. Los teseractos se doblan, la 16-celdas, son el equivalente del octaedro, pues son ambos politopos de cruz. Los politopos de 120 celdas y los de 600 celdas se doblan de igual modo, y son análogos al dodecaedro y al icosaedro, respectivamente. El de 24 celdas es un policrono regular único y que no tiene ningún equivalente tridimensional. Apenas pues la esfera, o 2-esfera, es una superficie de dos dimensiones curvada compuesta de todos los puntos equidistantes de un punto central dado, en un espacio tridimensional, la 3-esfera, una clase de hiperesfera, es el espacio que contiene todos los puntos equidistantes a un punto central dado, en un espacio cuadridimensional. Cada sección transversal tridimensional de un 3-esfera es un 2-esfera.
La analogía dimensional se usa frecuentemente para comprender el salto de una dimensión (en este caso, la tercera dimensión) a una más alta (cuarta dimensión). La analogía dimensional consiste en resolver un problema en n + 1 dimensiones relacionándolo primero con un problema análogo de (n - 1) dimensión, vale decir, "una dimensión menos". E igualmente debe analizarse el caso de cómo se relaciona el problema en n con el de (n + 1) dimensiones, es decir, "una más".
Edwin Abbott Abbott en su libro Planilandia (Flatland) escribe sobre un "ser cuadrado" que vive en un mundo de dos dimensiones, como la superficie de un pedazo de papel. Este "cuadrado" se enfrenta a experimentos de un ser tridimensional. El ser tridimensional es percibido por el "cuadrado" como un ser aparentemente divino, ya que puede poner y quitar objetos de una caja fuerte sin romperla ni abrirla (moviéndolos a través de su tercera dimensión), ver todo desde de la perspectiva de dos dimensiones sea incluido detrás de las paredes (puesto que ve "sobre" Planilandia), y totalmente invisible para los habitantes de Planilandia, puesto que está "arriba" y una dimensión por arriba de las dos dimensiones en las que el cuadrado está atrapado. No obstante, el ser tridimensional podría manifestarse en el mundo de dos dimensiones, pero sólo parcialmente, si fuera una esfera, aparecería como una secuencia de círculos sucesivos "que cambian de tamaño" (intersecciones de la esfera con el plano de dos dimensiones). Aplicando analogía dimensional, uno puede deducir que el ser cuadridimensional sería capaz de hazañas similares de nuestra perspectiva tridimensional.
Rudy Rucker demuestra esto en su novela "Spaceland", en la cual el protagonista encuentra los seres cuadridimensionales que demuestran tales energías. Un uso útil de la analogía dimensional en visualizar la cuarta dimensión está en la proyección. Una proyección es una manera para representar un objeto (n+1)-dimensional en la n-dimensión. Por ejemplo, las pantallas de computadora son de dos dimensiones, y todas las fotografías de objetos tridimensionales son representadas en dos dimensiones puesto que la información de la tercera dimensión (o de la profundidad) no puede ser representada por la pantalla (si el observador se mueve, aleje o acerque, la imagen no cambiará). En este caso, la profundidad se quita y se substituye por la información indirecta. La retina del ojo es un arsenal de dos dimensiones de receptores pero puede permitir que el cerebro perciba la naturaleza de objetos tridimensionales usando la información indirecta (como la perspectiva, el sombreado, visión binocular, etc.).
La perspectiva del uso de los artistas da profundidad tridimensional a los cuadros de dos dimensiones. Asimismo, los objetos en la cuarta dimensión se pueden proyectar matemáticamente a las familiares tres dimensiones, donde pueden entonces ser examinados más convenientemente. En este caso, la "retina de un ojo cuadridimensional" tendría un arsenal de receptores tridimensionales. El ser hipotético con tal ojo percibiría la naturaleza de objetos cuadridimensionales usando la información indirecta contenida en las imágenes que recibe en su retina. La proyección de la perspectiva a partir de cuatro dimensiones produce efectos similares como en el caso tridimensional, tal como la perspectiva.
Esto agrega "profundidad cuadridimensional" a estos cuadros tridimensionales. La analogía dimensional también ayuda a entender tales proyecciones. Por ejemplo, los objetos de dos dimensiones son limitados por límites unidimensionales: un cuadrado es limitado por cuatro bordes o líneas. Los objetos tridimensionales son limitados por superficies de bidimensionales: un cubo es limitado por 6 cuadrados. Aplicando analogía dimensional, uno puede deducir que un cubo cuadridimensional, conocido como teseracto, es limitado por los volúmenes tridimensionales.
Y de hecho, éste es el caso matemáticamente: el teseracto es limitado por 8 cubos. Saber esto es indispensable para entender cómo interpretar una proyección tridimensional del teseracto. Los límites del teseracto proyectan a los volúmenes en la imagen, superficies no simplemente de dos dimensiones. Esto ayuda a entender las características de dichas dimensiones que de otra manera sólo confundirían. De igual manera, el concepto de sombras puede ayudarnos mejor a entender la teoría de cuatro dimensiones. Si usted proyectara una luz sobre objeto tridimensional, éste proyectaría una sombra de dos dimensiones. Por lo tanto la luz en un objeto de dos dimensiones echaría una sombra unidimensional (en un mundo de dos dimensiones), y la luz en un objeto unidimensional en un mundo unidimensional echaría una sombra cero-dimensional, es decir, un punto de la no-luz. Esta idea se puede utilizar en la otra dirección; la luz en un objeto cuadridimensional proyectaría una sombra tridimensional. Como ejemplo, la sombra de un cubo transparente, proyectaría una sombra sobre el papel, de dos cuadrados, unidos por sus vértices con 4 segmentos.
Semejantemente, si era un cubo cuadridimensional iluminado con luz de 4 dimensiones, su sombra sería la de un cubo tridimensional dentro de otro cubo tridimensional. Siendo tridimensionales podemos solamente ver el mundo con nuestros ojos en dos dimensiones; el ser cuadridimensional consideraría el mundo en tres. Así podría, por ejemplo, ver los seis lados de una caja opaca simultáneamente. No solamente eso; también podría ver lo que hay al interior de la caja, como en Planilandia, en donde la esfera ve objetos en el mundo de dos dimensiones y todo dentro de ellos simultáneamente. Análogo, un espectador cuadridimensional vería todos los puntos en nuestro espacio tridimensional simultáneamente, incluyendo la estructura interna de objetos sólidos y de cosas obscurecidos de nuestro punto de vista.
Albert Einstein en su célebre teoría de 1905 de la relatividad especial habló por primera vez del tiempo como una cuarta dimensión y como algo indispensable para ubicar un objeto en el espacio y en un momento determinado. El tiempo en la teoría de la relatividad no es una dimensión espacial más, ya que fijado un punto del espacio-tiempo éste puede ser no alcanzable desde nuestra posición actual, hecho que difiere de la concepción usual de dimensión espacial. Aunque inicialmente se interpretó el tiempo como una "dimensión" matemática necesaria para ubicar un evento u objeto, en la teoría de la relatividad general el tiempo es tratado como una dimensión geométrica más, aunque los objetos materiales no puedan seguir una trayectoria completamente arbitraria a lo largo del tiempo (como por ejemplo "dar la vuelta" y viajar al pasado). La necesidad del tiempo dentro de la teoría de la relatividad es necesaria por dos motivos:
En primer lugar, los objetos no sólo se mueven a través del espacio sino que también lo hacen a través del tiempo, es decir su coordenada temporal aumenta continuamente, por lo que hubo la necesidad de hablar del tiempo ligado al espacio como la cuarta dimensión (en inglés spacetime, en castellano espacio-tiempo). Además el ritmo de avance en la dimensión temporal depende del estado de movimiento del observador, produciéndose una dilatación temporal efectiva para los observadores más rápidos en relación al tiempo medido por un observador estacionario.
En segundo lugar, el carácter intrínseco del espacio-tiempo y su cuatridimensionalidad requiere un modo conceptualmente diferente de tratar la geometría del universo, puesto que una cuarta dimensión implica un espacio plano (bidimensional) que se curva en la teoría de la relatividad general por la acción de la gravedad de la materia originándose la curvatura del espacio-tiempo.
Finalmente cabe añadir que algunas teorías físicas como la teoría de Kaluza-Klein y las teoría de supercuerdas, en sus varias versiones, añaden a las tres dimensiones físicas espaciales entre 1 y 9 dimensiones espaciales adicionales, de tipo compacto; además de la dimensión temporal.
|
|
|
|
|
 Primeira
Anterior
44 a 58 de 133
Seguinte
Última
|
|
| |
|
|
©2025 - Gabitos - Todos os direitos reservados | |
|
|
