|
|
General: NUMERO DE EULER EN FUNCION AL PI Y AL PHI
إختار ملف آخر للرسائل |
|
جواب |
رسائل 1 من 84 في الفقرة |
|
NUMERO DE EULER EN FUNCION AL PI Y AL PHI |
|
|
|
جواب |
رسائل 10 من 84 في الفقرة |
|
https://matelucia.wordpress.com/1-posicion-relativa-de-recta/3-6-prismas-y-piramides/ |
|
|
|
جواب |
رسائل 11 من 84 في الفقرة |
|
|
|
|
جواب |
رسائل 12 من 84 في الفقرة |
|
|
|
|
جواب |
رسائل 13 من 84 في الفقرة |
|
|
LA ISLA DE PASCUA O DE RAPA NUI ESTÁ SITUADA EN UN PARALELO DE LA ESFERA TERRESTRE CUYA PROYECCIÓN A LA ESFERA CELESTE ES EL PARALELO EN EL QUE ESTÁ EL PUNTO DEL CENTRO DE LA GALAXIA
|
 First First  Previous 2 to 4 of 4 Next Previous 2 to 4 of 4 Next  Last Last  |
|
|
| Reply |
Message 17 of 17 on the subject |
|
|
|
|
|
|
|
|
|
|
جواب |
رسائل 14 من 84 في الفقرة |
|
|
|
Suddenly I have this idea that PI, the Golden Ratio and Euler's number could form a right triangle. I was almost right. Perhaps that's worth for someone.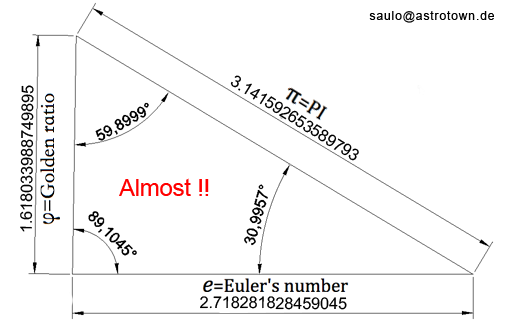
|
|
|
|
|
|
|
جواب |
رسائل 15 من 84 في الفقرة |
|
|
|
|
جواب |
رسائل 16 من 84 في الفقرة |
|
|
|
|
جواب |
رسائل 17 من 84 في الفقرة |
|
|
|
|
جواب |
رسائل 18 من 84 في الفقرة |
|
|
|
|
جواب |
رسائل 19 من 84 في الفقرة |
|
|
|
|
جواب |
رسائل 20 من 84 في الفقرة |
|
..the Sun oscillates up and down relative to the Galactic plane approximately 2.7 times per orbit. This is very similar to how a simple harmonic oscillator works with no drag force.
http://en.wikipedia.org/wiki/Milky_Way
|
|
|
|
جواب |
رسائل 21 من 84 في الفقرة |
|
|
|
|
جواب |
رسائل 22 من 84 في الفقرة |
|
Sixes - Proton and Neutron, Saturn, Easter Island, Mount Everest, Challenger Deep, Rome and Key Largo
Source - Secrets in Plain Sight
“The comb of the hive-bee, as far as we can see, is absolutely perfect in economizing labour and wax.” -Charles Darwin
 Euclid recognized that the hexagon shape makes most efficient use of material in space. The Pantheon dome is an Roman architectural wonder made possible by its interior honeycomb structural ribbing. Modern man-made honeycomb materials are widely used in the aerospace industry because they offer high strength-to-weight ratios. Speaking of aerospace, the Cassini spacecraft photographed the north pole of Saturn in 2013 and humanity got a glimpse of an enormous persistent hexagonal pattern in this gas giant.
 |
| NASA/JPL/SSI |
I have had a series of epiphanies recently regarding the structure of the Earth. It all started with my post Deep Challenges when I found patterns of sixes in the measures of the highest and largest mountains, the deepest place on Earth, and Easter Island.  Incidentally, a line from Easter Island to the obelisk in St. Peter’s Square incredibly bisects the whole Vatican complex. The name “Easter Island” was given by the island’s first recorded European visitor, the Dutch explorer Jacob Roggeveen, who encountered it on Easter Sunday, 5 April 1722. WTF?  On the flipside, Urban Asplund discovered that Africa is 66.6° wide from its westernmost point in Dakar to the easternmost projection of Somalia. Africa is also 66.6° high from its southernmost point to the place where the line running due north hits the Mediterranean, near Benghazi.  The Earth’s axis is also tilted 66.6° (90 – 23.4 = 66.6) from the ecliptic and travels along it at 66600 miles/hour (99.9%). South America is 66.6° long along a north-south path that passes through Mt. Aconcagua, its highest peak. Urban Asplund discovered this one too.  The distance between the tips of South America and Africa is ~6660 km.  North America is 66.66° wide from the tip of Florida at Key Largo to the farthest place the US reaches into the Bearing Straight, Yesterday Island. The adjacent island, Tomorrow Island, is owned by Russia and is only a stone’s throw away on the other side of the International Dateline. Strange but true! Sea level changes over time, the Earth’s continents move, land subsides and uplifts. All of these correlations are the situation right NOW.  Eurasia is also structured with sixes but this time the measurement is 6066 nautical miles from the southwestern most point in Europe, the lighthouse at Cape St. Vincent, to the symbolic Haicang bridge in Xiamen China. The lines goes very close to, but not perfectly through Astana, Kazakhstan.
“Cape St. Vincent was already sacred ground in Neolithic times, as standing menhirs in the neighborhood attest. The ancient Greeks called it Ophiussa (Land of Serpents), inhabited by the Oestriminis and dedicated here a temple to Heracles. The Romans called it Promontorium Sacrum (or Holy Promontory). They considered it a magical place where the sunset was much larger than anywhere else. They believed the sun sank here hissing into the ocean, marking the edge of their world.” - SourceThat’s apropos considering how I previously connected snakes and sixes in Serpent Wisdom. In 1541, European traders (mainly Portuguese) first visited Xiamen, which was China’s main port in the nineteenth century for exporting tea. Funny that they were Portuguese, considering where the opposite endpoint is in this measure of the maximum width of Eurasia. The Portuguese really got around back then! All these sixes remind me of something I noticed in the microcosm of matter itself. Every proton in the universe is made of 2 up quarks and 1 down quark. The charge on the up quark is +0.666666… and the charge on the down quark is -0.333333…, netting a charge of +0.999999…, polarized oppositely to the electron. The neutron has 1 up quark and 2 down quarks as you can see, netting a zero charge.  In the macrocosm, I noticed the equation that governs Earth’s gravitational sphere of influence is all threes. The Sun’s mass is 333000 times greater than Earth’s mass. AU stands for astronomical unit, the mean distance from the Earth to the Sun.  Repetitive sixes and threes suggest triangles. This leads me finally to another epiphany (e-π-Φ-ny) I had, that the infinitesimal gap in what would otherwise be a perfect Pythagorean triangle connecting e, π, and Φ suggests the question, “Why can’t we ever rationalize the transcendental?”
 |
| This mystery is drawn to scale |
Logically, the answer is that it is an irreducible eternal mystery, and I’m down with that.
|
|
|
|
جواب |
رسائل 23 من 84 في الفقرة |
|
Sixes - Proton and Neutron, Saturn, Easter Island, Mount Everest, Challenger Deep, Rome and Key Largo
Source - Secrets in Plain Sight
“The comb of the hive-bee, as far as we can see, is absolutely perfect in economizing labour and wax.” -Charles Darwin
 Euclid recognized that the hexagon shape makes most efficient use of material in space. The Pantheon dome is an Roman architectural wonder made possible by its interior honeycomb structural ribbing. Modern man-made honeycomb materials are widely used in the aerospace industry because they offer high strength-to-weight ratios. Speaking of aerospace, the Cassini spacecraft photographed the north pole of Saturn in 2013 and humanity got a glimpse of an enormous persistent hexagonal pattern in this gas giant.
 |
| NASA/JPL/SSI |
I have had a series of epiphanies recently regarding the structure of the Earth. It all started with my post Deep Challenges when I found patterns of sixes in the measures of the highest and largest mountains, the deepest place on Earth, and Easter Island.  Incidentally, a line from Easter Island to the obelisk in St. Peter’s Square incredibly bisects the whole Vatican complex. The name “Easter Island” was given by the island’s first recorded European visitor, the Dutch explorer Jacob Roggeveen, who encountered it on Easter Sunday, 5 April 1722. WTF?  On the flipside, Urban Asplund discovered that Africa is 66.6° wide from its westernmost point in Dakar to the easternmost projection of Somalia. Africa is also 66.6° high from its southernmost point to the place where the line running due north hits the Mediterranean, near Benghazi.  The Earth’s axis is also tilted 66.6° (90 – 23.4 = 66.6) from the ecliptic and travels along it at 66600 miles/hour (99.9%). South America is 66.6° long along a north-south path that passes through Mt. Aconcagua, its highest peak. Urban Asplund discovered this one too.  The distance between the tips of South America and Africa is ~6660 km.  North America is 66.66° wide from the tip of Florida at Key Largo to the farthest place the US reaches into the Bearing Straight, Yesterday Island. The adjacent island, Tomorrow Island, is owned by Russia and is only a stone’s throw away on the other side of the International Dateline. Strange but true! Sea level changes over time, the Earth’s continents move, land subsides and uplifts. All of these correlations are the situation right NOW.  Eurasia is also structured with sixes but this time the measurement is 6066 nautical miles from the southwestern |
|
|
|
جواب |
رسائل 24 من 84 في الفقرة |
|
Sólido de Kepler-Poinsot
Los sólidos de Kepler-Poinsot con sus símbolos de Schläfli.
Un sólido de Kepler (también llamado sólido de Kepler-Poinsot) es un poliedro regular no convexo, cuyas caras son todas polígonos regulares y que tiene en todos sus vértices el mismo número de caras concurrentes (compárese con los sólidos platónicos).
Existen sólo cuatro tipos, con las denominaciones siguientes:
Las caras están solo parcialmente en la superficie del sólido, y las partes expuestas están sólo conectadas en puntos (si están conectadas de algún modo). Si las partes se cuentan como caras separadas, el sólido deja de ser regular.
Características
Un sólido de Kepler cubre su esfera circunscrita más de una vez (con una esfera interior y otra exterior), con los centros de las caras como puntos direccionales en los sólidos que tienen caras en forma de pentagrama, mientras que en los otros son los vértices los que cumplen esa función. Por esta razón, no son necesariamente equivalentes topológicos de la esfera como lo son los sólidos platónicos, y en particular la característica de Euler V − E + F = 2 se verifica solamente para el Gran dodecaedro estrellado y para el Gran icosaedro.
Esto dependerá de cómo se observe el poliedro. Considérese, por ejemplo, el pequeño dodecaedro estrellado.1 Consiste en un dodecaedro con una pirámide pentagonal en cada una de sus 12 caras. En consecuencia, las 12 caras se extienden a pentagramas con el pentágono central dentro del sólido. La parte externa de cada cara consiste en cinco triángulos conectados por sólo cinco puntos. Si se cuentan separadamente, hay 60 caras (pero estas son triángulos isósceles que no son polígonos regulares, en cuyo caso seria un pentaquisdodecaedro). De modo similar, cada lado puede ser contado como tres, pero entonces los habrá de dos tipos. Igualmente, con los "cinco puntos" antes mencionados: en total habrá 20 puntos que pueden contarse como vértices, por lo que habrá un total de 32 vértices (otra vez, de dos tipos). Ahora la ecuación de Euler se verifica: 60 - 90 + 32 = 2.
Tipos
Hay cuatro sólidos de Kepler distintos:
Los dos primeros son estrellamientos, es decir, sus caras son convexas. Los otros dos tienen caras cóncavas, pero cada par de caras que se encuentra en un vértice de hecho lo hace en dos.
Historia
Mosaico del suelo en la basílica de San Marcos, a veces atribuido a Paolo Uccello.
La mayoría de los poliedros de Kepler-Poinsot, si no todos, eran ya conocidos de una forma u otra antes de Kepler. Un pequeño dodecaedro estrellado aparece en una tarsia de mármol (panel de incrustaciones) en el suelo de la basílica de San Marcos de Venecia, Italia. Data del siglo XV y, a veces se atribuye a Paolo Uccello. Wenzel Jamnitzer, en su obra Perspectiva corporum regularium (Perspectivas de los sólidos regulares), un libro de grabados en madera publicado en el siglo XVI, representa el gran dodecaedro y el gran dodecaedro estrellado.2 Se desprende de la disposición general del libro que consideraba solamente los cinco sólidos platónicos como regulares, y no comprendía la naturaleza periódica de sus grandes dodecaedros.
El pequeño y gran dodecaedro estrellado, a veces llamados poliedros de Kepler, fueron reconocidos por primera vez como regulares por Johannes Kepler en 1619, cuando notó que los dodecaedros estrellados (tanto el grande como el pequeño) se componían de dodecaedros "ocultos" (con caras pentagonales) que tienen caras compuestas de triángulos, tomando la apariencia de estrellas estilizadas. Los obtuvo por estelación del dodecaedro regular convexo, por primera vez, tratándolo como una superficie en lugar de un sólido. Se dio cuenta de que extendiendo los bordes o caras del dodecaedro convexo hasta que se encontrasen de nuevo, se podían obtener pentágonos estrellados. De esta manera construyó los dos dodecaedros estrellados, cada uno con la región convexa central de cada cara "oculta" en el interior, sólo con los brazos triangulares visibles. El paso final de Kepler fue reconocer que estos poliedros se ajustaban a la definición de regularidad, aunque fueran cóncavos en lugar de convexos, como sí lo eran los tradicionales sólidos platónicos.
En 1809, Louis Poinsot redescubrió las figuras de Kepler, mediante el ensamblaje de pentágonos estrellados alrededor de cada vértice. También montó polígonos convexos alrededor de los vértices de las estrellas para descubrir dos estrellas más regulares, el gran icosaedro y el gran dodecaedro. Por ello, algunos llaman a estos dos los poliedros de Poinsot. Poinsot no sabía si había descubierto todos los poliedros regulares estrellados.
Tres años más tarde, Augustin Cauchy demostró que la lista por estelación de los sólidos platónicos estaba completa, y casi medio siglo después, en 1858, Joseph Louis François Bertrandproporcionó una prueba más elegante por facetado de ellas.
Al año siguiente, Arthur Cayley dio a los poliedros de Kepler–Poinsot los nombres por los que generalmente conocidos hoy.
Unos cien años más tarde, John Conway desarrolló una terminología sistemática para las estelaciones hasta un máximo de cuatro dimensiones. Dentro de este esquema, sugirió nombres ligeramente modificados para dos de los poliedros regulares estrellados. Los nombres de Conway han sido considerados de utilidad, pero no han sido ampliamente adoptados.
| Nombre de Cayley |
pequeño dodecaedro estrellado |
gran dodecaedro |
gran dodecaedro estrellado |
gran icosaedro |
| Nombre de Conway |
dodecaedro estrellado |
gran dodecaedro (sin cambio) |
dodecaedro grande estrellado |
gran icosaedro (sin cambio) |
https://es.wikipedia.org/wiki/S%C3%B3lido_de_Kepler-Poinsot |
|
|
 First First  Previous 2 to 5 of 5 Next Previous 2 to 5 of 5 Next  Last Last  |
|
|
Posted in Azulejos-Mosaicos, Italia, Templo with tags Poliedros on 7 junio 2012 by angelrequena

Hace tiempo hablamos del conocido pequeño dodecaedro estrellado del pavimento de la puerta de salida derecha del duomo de San Marcos. No es el único de la catedral veneciana: apenas visible para la visita ordinaria hay otro más pequeño, justo debajo del iconostasio en su centro, en lugar preferente y en línea con el altar.
Si se entra hacia la Pala de Oro puede verse una mancha central en la lejanía pero casi sin distinguirse. En mi última visita tuve la gran suerte de encontrar un ordenanza amable que encendía las luces a un grupo concertado que me permitió verlo y fotografiarlo. No desmerece de su hermano mayor, si cabe revela mayor virtuosismo y ostentación del dominio de la perspectiva matemática.
Hay cuatro sólidos regulares cóncavos, los dos de Poinsot y los dos de Kepler. Venecia nos ofrece los dos de Kepler en San Pantaleone y uno en San Marcos pero en dos lugares, uno alejado para despedirse del templo y otro en el lugar más destacado: la entrada central al recinto más sagrado.
El dodecaedro estrellado de la puerta (abajo) solo tiene una corona de taracea marmórea complementaria mientras que el del iconostasio (arriba) tiene tres.

3 Comments »
https://mateturismo.wordpress.com/tag/poliedros/page/7/
|
|
|
|
|
|
 أول أول
 سابق
10 a 24 de 84
لاحق سابق
10 a 24 de 84
لاحق آخر
آخر
|
|
| |
|
|
©2026 - Gabitos - كل الحقوق محفوظة | |
|
|

